【数据结构】11 堆栈（顺序存储和链式存储）

news/2024/7/27 9:05:26/文章来源:https://blog.csdn.net/vox520/article/details/136081824

定义

可认为是具有一定约束的线性表，插入和删除操作都在一个称为栈顶的端点位置。也叫后入先出表（LIFO）
类型名称：堆栈（STACK）
数据对象集： 一个有0个或者多个元素的有穷线性表。
操作集：
（1）Stack CreateStack( int MaxSize)
生成空堆栈，其最大长度为MaxSize
（2）bool IsFull(Stack)
判断栈S是否已满。
（3）bool Push(Stack S, ElementType X)
将元素X压入堆栈
（4）ElementType Pop(Stack S)
删除并返回栈顶元素

例3.5 如果将abcd四个字符按顺序压入堆栈，是否可能产生cabd这样的序列，共可能产生多少种输出？
一个字符出入栈：只可能是A进——A出
两个字符出入栈： 2种情况
A进A出 B进B出
A进B进 B出A出
三个字符出入栈： 5种情况
A进B进C进 C出B出A出
A进B进 B出 C进 C出
A进B进 B出A出 C进C出
A进A出 B进B出 C进C出
A进A出 B进C进 C出B出
四个字符： 14种情况

  1. A在第一位出 A_ _ _
    对应3个字符出入栈 -5种情况
  2. A在第二位 _ A _ _
    只能B出来后A才能出 BA_ _
    对应2个字符出入栈 -2种情况
  3. A在第三位 _ _ A _
    前两位必是 B或者C
    最后一位必是D
    2种情况
  4. A在第四位 _ _ _ A
    对应三个字符出入栈 5种情况

堆栈的实现

顺序栈的实现

由一个一维数组和一个记录栈顶元素位置的变量组成，另外还有一个记录堆栈最大容量的变量MaxSize。
习惯将栈底放在数组下标小的那端，栈顶位置用一个整型变量Top记录当前栈顶元素的下标值。当Top指向-1时，表示空栈；当Top指向MaxSize-1时表示栈满。
顺序栈类型Stack表示如下：

typedef int ElementType;
typedef int Position;
typedef struct SNode* PtrToSNode;struct SNode {ElementType* Data;Position Top;int MaxSize;};typedef PtrToSNode Stack;

顺序栈的创建

Stack CreateStack(int MaxSize) {Stack S = (Stack)malloc(sizeof(SNode) * 1);S->Data = (ElementType * )malloc(sizeof(ElementType) * MaxSize);S->Top = -1;S->MaxSize = MaxSize;return S;
}

进栈


bool IsFull(Stack S) {if (S->Top == S->MaxSize - 1) {return true;}return false;
}bool Push(Stack S, ElementType X) {if (IsFull(S)) {printf("The Stack is full!\n");return false;}(S->Top)++;S->Data[S->Top] = X;return true;}

出栈

bool IsEmpty(Stack S) {if (S->Top == -1) {return true;}return false;
}ElementType Pop(Stack S) {if (IsEmpty(S)) {printf("The Stack is empty!\n");return -1;}int temp = S->Data[S->Top];(S->Top)--;return temp;}

完整代码

# include <stdio.h>
#include < stdlib.h>typedef int ElementType;
typedef int Position;
typedef struct SNode* PtrToSNode;struct SNode {ElementType* Data;Position Top;int MaxSize;};typedef PtrToSNode Stack;Stack CreateStack(int MaxSize) {Stack S = (Stack)malloc(sizeof(SNode) * 1);S->Data = (ElementType * )malloc(sizeof(ElementType) * MaxSize);S->Top = -1;S->MaxSize = MaxSize;return S;
}bool IsFull(Stack S) {if (S->Top == S->MaxSize - 1) {return true;}return false;
}bool Push(Stack S, ElementType X) {if (IsFull(S)) {printf("The Stack is full!\n");return false;}/*(S->Top)++;S->Data[S->Top] = X;*/S->Data[++(S->Top)] = X;return true;}bool IsEmpty(Stack S) {if (S->Top == -1) {return true;}return false;
}ElementType Pop(Stack S) {if (IsEmpty(S)) {printf("The Stack is empty!\n");return -1;}/*int temp = S->Data[S->Top];(S->Top)--;return temp;*/return (S->Data[(S->Top)--]);}void print_s(Stack S) {int t = S->Top;while (t != -1) {printf("Node: %d\n", S->Data[t]);(t)--;}
}int main() {Stack S = NULL;int MaxSize = 10;S = CreateStack(MaxSize);ElementType X;int N;scanf_s("%d", &N);while (N--) {scanf_s("%d", &X);if (Push(S, X) == false) {printf("Push error!\n");}}print_s(S);int out = Pop(S);printf("out : %d\n", out);print_s(S);}

用一个数组实现两个堆栈

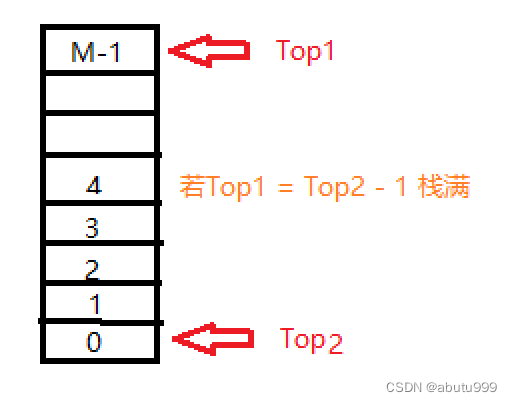
在这里插入图片描述

结构体
typedef struct DSNode* DStack;
struct DSNode
{ElementType* Data;Position Top1;Position Top2;int MaxSize;
};
创建
DStack CreateDStack(int MaxSize) {DStack S = (DStack)malloc(sizeof(DSNode) * 1);S->Data = (ElementType*)malloc(sizeof(ElementType) * MaxSize);S->Top2 = -1;S->Top1 = MaxSize;S->MaxSize = MaxSize;return S;
}
入栈

bool PushX(DStack S, ElementType X, int Tag) {if (S->Top1 - S->Top2 == 1) {printf("the stack is full!\n");return false;}if (Tag == 1) {(S->Top1)--;S->Data[S->Top1] = X;}else{(S->Top2)++;S->Data[S->Top2] = X;}return true;
}
出栈

ElementType PopX(DStack S, int Tag) {if (Tag == 1) {if (S->Top1 == S->MaxSize) {printf("the stack1 is empty!\n");return -1;}else {return S->Data[(S->Top1)++];}}else {if (S->Top2 == -1) {printf("the stack2 is empty!\n");return -1;}else {return S->Data[(S->Top2)--];}}}
完整代码
# include <stdio.h>
#include < stdlib.h>typedef int ElementType;
typedef int Position;typedef struct DSNode* DStack;
struct DSNode
{ElementType* Data;Position Top1;Position Top2;int MaxSize;
};DStack CreateDStack(int MaxSize) {DStack S = (DStack)malloc(sizeof(DSNode) * 1);S->Data = (ElementType*)malloc(sizeof(ElementType) * MaxSize);S->Top2 = -1;S->Top1 = MaxSize;S->MaxSize = MaxSize;return S;
}bool PushX(DStack S, ElementType X, int Tag) {if (S->Top1 - S->Top2 == 1) {printf("the stack is full!\n");return false;}if (Tag == 1) {(S->Top1)--;S->Data[S->Top1] = X;}else{(S->Top2)++;S->Data[S->Top2] = X;}return true;
}ElementType PopX(DStack S, int Tag) {if (Tag == 1) {if (S->Top1 == S->MaxSize) {printf("the stack1 is empty!\n");return -1;}else {return S->Data[(S->Top1)++];}}else {if (S->Top2 == -1) {printf("the stack2 is empty!\n");return -1;}else {return S->Data[(S->Top2)--];}}}void print_ds(DStack S) {printf("print S1:\n");int t = S->Top1;while (t != S->MaxSize) {printf("Node: %d\n", S->Data[t]);(t)++;}printf("print S2:\n");t = S->Top2;while (t != -1) {printf("Node: %d\n", S->Data[t]);(t)--;}
}int main() {int MAXSIZE = 10;DStack S = CreateDStack(MAXSIZE);ElementType X;int N;scanf_s("%d", &N);while (N--) {scanf_s("%d", &X);if (PushX(S, X, 1) == false) {printf("Push error!\n");}if (PushX(S, X, 2) == false) {printf("Push error!\n");}}print_ds(S);int out = PopX(S,1);printf("out : %d\n", out);print_ds(S);}

链式存储的实现

栈顶指针Top就是链表的栈顶结点，栈中的其他结点通过他们的指针Next链接起来，栈底结点的Next为NULL

数据结构

typedef int ElementType;
typedef struct SNode* PtrToSNode;struct SNode {ElementType Data;PtrToSNode Next;
};typedef PtrToSNode Stack;

创建


Stack CreateStack(Stack S) {S = (Stack)malloc(sizeof(SNode) * 1);S->Next = NULL;return S;
}

入栈


bool Push(Stack S, ElementType X) {Stack temp = (Stack)malloc(sizeof(SNode));temp->Data = X;temp->Next = S->Next;S->Next = temp;return true;}

出栈

ElementType Pop(Stack S) {if (S->Next == NULL) {printf("the stack is empty!\n");return -1;}ElementType re = S->Next->Data;S->Next = S->Next->Next;return re;}

完整代码

# include <stdio.h>
#include < stdlib.h>typedef int ElementType;
typedef struct SNode* PtrToSNode;struct SNode {ElementType Data;PtrToSNode Next;
};typedef PtrToSNode Stack;Stack CreateStack(Stack S) {S = (Stack)malloc(sizeof(SNode) * 1);S->Next = NULL;return S;
}bool Push(Stack S, ElementType X) {Stack temp = (Stack)malloc(sizeof(SNode));temp->Data = X;temp->Next = S->Next;S->Next = temp;return true;}ElementType Pop(Stack S) {if (S->Next == NULL) {printf("the stack is empty!\n");return -1;}ElementType re = S->Next->Data;S->Next = S->Next->Next;return re;}void prints(Stack S) {Stack t = S->Next;while (t != NULL) {printf("Node: %d\n", t->Data);t = t->Next;}
}int main() {Stack S = NULL;S = CreateStack(S);ElementType X;int N;scanf_s("%d", &N);while (N--) {scanf_s("%d", &X);if (Push(S, X) == false) {printf("Push error!\n");}}prints(S);ElementType out = Pop(S);printf("out : %d\n", out);prints(S);}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.luyixian.cn/news_show_963370.aspx

如若内容造成侵权/违法违规/事实不符，请联系dt猫网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

探索现代Web前端开发框架：选择最适合你的工具

探索现代Web前端开发框架：选择最适合你的工具

在当今快速发展的Web开发领域&#xff0c;前端开发框架的选择显得尤为关键。这些框架可以帮助我们更高效地构建出交互性强、性能卓越的用户界面。本文将带你了解几个当前最受欢迎的Web前端开发框架&#xff0c;并帮助你根据自己的需求选择最合适的工具。 1. React React由Fac…
阅读更多...
sheng的学习笔记-网络爬虫scrapy框架

sheng的学习笔记-网络爬虫scrapy框架

基础知识&#xff1a; scrapy介绍 何为框架&#xff0c;就相当于一个封装了很多功能的结构体&#xff0c;它帮我们把主要的结构给搭建好了&#xff0c;我们只需往骨架里添加内容就行。scrapy框架是一个为了爬取网站数据&#xff0c;提取数据的框架&#xff0c;我们熟知爬虫总…
阅读更多...
新年福利：《YOLO目标检测》送书活动

新年福利：《YOLO目标检测》送书活动

博主简介 AI小怪兽&#xff0c;YOLO骨灰级玩家&#xff0c;1&#xff09;YOLOv5、v7、v8优化创新&#xff0c;轻松涨点和模型轻量化&#xff1b;2&#xff09;目标检测、语义分割、OCR、分类等技术孵化&#xff0c;赋能智能制造&#xff0c;工业项目落地经验丰富&#xff1b; …
阅读更多...
docker 基于容器创建本地web容器化镜像

docker 基于容器创建本地web容器化镜像

一、docker 基于容器创建本地web容器化镜像 1、启动指定buysbox 镜像 docker run --name b1 -it busybox:latest 2、创建目录&#xff0c;并创建html mkdir -p /data/html vi index.html 内容自定义例如&#xff1a;<h1>welcome to busybox<h1> 3、新增窗口&am…
阅读更多...
【JVM篇】ThreadLocal中为什么要使用弱引用

【JVM篇】ThreadLocal中为什么要使用弱引用

文章目录 &#x1f354;ThreadLocal中为什么要使用弱引用⭐总结 &#x1f354;ThreadLocal中为什么要使用弱引用 ThreadLocal可以在线程中存放线程的本地变量&#xff0c;保证数据的线程安全 ThreadLocal是这样子保存对象的&#xff1a; 在每个线程中&#xff0c;存放了一个…
阅读更多...
3D高斯溅射：面向三维场景的实时渲染技术

3D高斯溅射：面向三维场景的实时渲染技术

1. 前言 高斯溅射技术【1】一经推出&#xff0c;立刻引起学术界和工业界的广泛关注。相比传统的隐式神经散射场渲染技术&#xff0c;高斯溅射依托椭球空间&#xff0c;显性地表示多目图像的三维空间关系&#xff0c;其计算效率和综合性能均有较大的提升&#xff0c;且更容易理…
阅读更多...
Java+SpringBoot：高校竞赛管理新篇章

Java+SpringBoot：高校竞赛管理新篇章

✍✍计算机编程指导师 ⭐⭐个人介绍&#xff1a;自己非常喜欢研究技术问题&#xff01;专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目&#xff1a;有源码或者技术上的问题欢迎在评论区一起讨论交流&#xff01; ⚡⚡ Java实战 |…
阅读更多...
使用client-only 解决组件不兼容SSR问题

使用client-only 解决组件不兼容SSR问题

目录 前言 一、解决方案 1.基于Nuxt 框架的SSR应用 2.基于vue2框架的应用 3.基于vue3框架的应用 二、总结 往期回顾 前言 最近在我的单页面SSR应用上开发JSON编辑器功能&#xff0c;在引入组件后直接客户端跳转OK&#xff0c;但是在直接加载服务端渲染的时候一直报这…
阅读更多...
【flink状态管理（三）】StateBackend的整体设计、StateBackend创建说明

【flink状态管理（三）】StateBackend的整体设计、StateBackend创建说明

文章目录 一. 状态后端概述二. StateBackend的整体设计1. 核心功能2. StateBackend的UML3. 小结 三. StateBackend的加载与初始化1. StateBackend创建概述2. StateBackend创建过程 一. 状态后端概述 StateBackend作为状态存储后端&#xff0c;提供了创建和获取KeyedStateBacke…
阅读更多...
postgresql 手动清理wal日志的101个坑

postgresql 手动清理wal日志的101个坑

新年的第一天&#xff0c;总结下去年遇到的关于WAL日志清理的101个坑&#xff0c;以及如何相对安全地进行清理。前面是关于WAL日志堆积的原因分析&#xff0c;清理相关可以直接看第三部分。 首先说明&#xff0c;手动清理wal日志是一个高风险的操作&#xff0c;尤其对于带主从的…
阅读更多...
前端vite+vue3——自动化配置路由布局

前端vite+vue3——自动化配置路由布局

文章目录 ⭐前言&#x1f496;vue3系列文章 ⭐ 自动化配置路由&#x1f496;引入vite版本自定义目录映射&#x1f496;自动化读取文件下的路由&#x1f496;main入口加载路由&#x1f496;入口app.vue配置&#x1f496;layout基础布局配置&#x1f496;效果 ⭐总结⭐结束 ⭐前言…
阅读更多...
搜索二维矩阵[中等]

搜索二维矩阵[中等]

一、题目 给你一个满足下述两条属性的m x n整数矩阵&#xff1a; 【1】每行中的整数从左到右按非严格递增顺序排列。 【2】每行的第一个整数大于前一行的最后一个整数。 给你一个整数target&#xff0c;如果target在矩阵中&#xff0c;返回true&#xff1b;否则&#xff0c;返…
阅读更多...
【Linux技术宝典】Linux入门：揭开Linux的神秘面纱

【Linux技术宝典】Linux入门：揭开Linux的神秘面纱

文章目录 官网Linux 环境的搭建方式一、什么是Linux&#xff1f;二、Linux的起源与发展三、Linux的核心组件四、Linux企业应用现状五、Linux的发行版本六、为什么选择Linux&#xff1f;七、总结 Linux&#xff0c;一个在全球范围内广泛应用的开源操作系统&#xff0c;近年来越来…
阅读更多...
树莓派编程基础与硬件控制

树莓派编程基础与硬件控制

1.编程语言 Python 是一种泛用型的编程语言&#xff0c;可以用于大量场景的程序开发中。根据基于谷歌搜 索指数的 PYPL&#xff08;程序语言流行指数&#xff09;统计&#xff0c;Python 是 2019 年 2 月全球范围内最为流行 的编程语言 相比传统的 C、Java 等编程语言&#x…
阅读更多...
生成树技术华为ICT网络赛道

生成树技术华为ICT网络赛道

9.生成树 目录 9.生成树 9.1.生成树技术概述 9.2.STP的基本概念及工作原理 9.3.STP的基础配置 9.4.RSTP对STP的改进 9.5.生成树技术进阶 9.1.生成树技术概述 技术背景&#xff1a;二层交换机网络的冗余性与环路 典型问题1&#xff1a;广播风暴 典型问题2&#xff1a;MA…
阅读更多...
《UE5_C++多人TPS完整教程》学习笔记10 ——《P11 设置加入游戏会话（Setup for Joining Sessions）》

《UE5_C++多人TPS完整教程》学习笔记10 ——《P11 设置加入游戏会话（Setup for Joining Sessions）》

本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P11 设置加入游戏会话&#xff08;Setup for Joining Sessions&#xff09;》 的学习笔记&#xff0c;该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版&#xff0c;UP主&…
阅读更多...
Linux开发：PAM1 介绍

Linux开发：PAM1 介绍

PAM（Pluggable Authentication Modules ）是Linux提供的一种通用的认证方式，他可以根据需要动态的加载认证模块，从而减少认证开发的工作量以及提供认证的灵活度。 1.PAM的框架 PAM的框架由一下几个部分构成 1)应用程序，即需要使用认证服务的程序，这些应用程序是使用抽象…
阅读更多...
单例模式 C++

单例模式 C++

6 种 单例 的手写&#xff0c;都是懒汉&#xff08;饿汉代码在 “懒汉 / 饿汉的区别”&#xff09; 目录 ✊前言 &#x1f33c;GPT解析 &#x1f33c;概念解析 RAII 懒汉 / 饿汉的区别 特点 举例 单例 -- 伪代码 适用场景 单例 -- 实现方式 优缺点 &#x1f382;手…
阅读更多...
【Iceberg学习二】Branch和Tag在Iceberg中的应用

【Iceberg学习二】Branch和Tag在Iceberg中的应用

Iceberg 表元数据保持一个快照日志&#xff0c;记录了对表所做的更改。快照在 Iceberg 中至关重要&#xff0c;因为它们是读者隔离和时间旅行查询的基础。为了控制元数据大小和存储成本&#xff0c;Iceberg 提供了快照生命周期管理程序&#xff0c;如 expire_snapshots&#xf…
阅读更多...
《Linux 简易速速上手小册》第9章: 备份与恢复策略（2024 最新版）

《Linux 简易速速上手小册》第9章: 备份与恢复策略（2024 最新版）

文章目录 9.1 理解备份的重要性9.1.1 重点基础知识9.1.2 重点案例&#xff1a;数据中心遭受火灾9.1.3 拓展案例&#xff1a;个人电脑硬盘故障9.1.4 企业级数据库被恶意软件加密 9.2 实施备份策略9.2.1 重点基础知识9.2.2 重点案例&#xff1a;为中小企业实施备份策略9.2.3 拓展…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023

友情链接： 我的编程经验分享 一条长河网 尧图网站开发 尧图建网站 广利置业