文章目录
- 整除分块的思考与运用
- 整除分块的时间复杂度证明 & 分块数量
- 整除分块的公式 & 公式证明
- 公式证明
- 代码code↓
整除分块的思考与运用
整除分块是为了解决一个整数求和问题
题目的问题为: ∑ i = 1 n ⌊ n i ⌋ \sum_{i=1}^{n} \left \lfloor \frac{n}{i} \right \rfloor i=1∑n⌊in⌋
求出上述式子的值为多少?
上述问题等同于 c o d e code code↓
int sum=0;
for(int i=1;i<=n;i++) sum+=n/i;//int是整除类型,所以可以直接整除
return sum;
注意事项: ⌊ x ⌋ \left \lfloor x \right \rfloor ⌊x⌋代表不大于 x x x 的最大整数,也可以成为向下取整
我们不难看出,如果我们直接按题意暴力模拟,则时间复杂度为 O ( n ) O(n) O(n),如果 n n n 比较大就会超时(TLE警告QWQ)
而如果我们将 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ ( 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n) 的值输出一下,就会发现其中有许多值是重复的
输出 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋值的 c o d e code code↓
for(int i=1;i<=n;i++) cout<<n/i<<endl;
我们可以举例来看一下:
我们令 n = 8 n=8 n=8 ,则有
| i i i 的值 | i i i = 1 1 1 | i i i = 2 2 2 | i i i = 3 3 3 | i i i = 4 4 4 | i i i = 5 5 5 | i i i = 6 6 6 | i i i = 7 7 7 | i i i = 8 8 8 |
|---|---|---|---|---|---|---|---|---|
| ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 的值 | 8 8 8 | 4 4 4 | 2 2 2 | 2 2 2 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 |
此时我们可以明显的看出 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 的值被明显的分成了几个块,每个块中的块值相同
| 分块 | [ 1 , 1 ] [1,1] [1,1] | [ 2 , 2 ] [2,2] [2,2] | [ 3 , 4 ] [3,4] [3,4] | [ 5 , 8 ] [5,8] [5,8] |
|---|---|---|---|---|
| 块值 | 8 8 8 | 4 4 4 | 2 2 2 | 1 1 1 |
整除分块的时间复杂度证明 & 分块数量
总共需要分少于 2 n 2 \sqrt{n} 2n种块,证明如下:
i ≤ n i \leq n i≤n 时, n i \frac{n}{i} in 的值有 { n 1 , n 2 , n 3 . . . n n } \left \{ \frac{n}{1} ,\frac{n}{2},\frac{n}{3} ...\frac{n}{\sqrt{n} }\right \} {1n,2n,3n...nn}, n i ≥ n \frac{n}{i} \ge \sqrt{n} in≥n,共 n \sqrt{n} n 个,此时 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 有 n \sqrt{n} n 种取值
i ≥ n i \ge n i≥n 时,有 n i ≤ n \frac{n}{i} \le \sqrt{n} in≤n,此时 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 也有 n \sqrt{n} n 种取值
两者相加,共 2 n 2 \sqrt{n} 2n种,所以整除分块的数量为 O ( n ) O(\sqrt{n}) O(n) 种,所以整除分块的时间复杂度为 O ( n ) O(\sqrt{n}) O(n)
整除分块的公式 & 公式证明
结论: R = n ⌊ n L ⌋ R=\frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} R=⌊Ln⌋n
每个块中的元素个数为: ( R − L + 1 ) (R-L+1) (R−L+1)
每个块中元素的 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 值为 ⌊ n L ⌋ \left \lfloor \frac{n}{L} \right \rfloor ⌊Ln⌋
每个块中的和为 a n s = ( R − L + 1 ) × ⌊ n L ⌋ ans=(R-L+1) \times \left \lfloor \frac{n}{L} \right \rfloor ans=(R−L+1)×⌊Ln⌋
公式证明
整除分块出现在能被 n n n 完全整除的数之后,到下一个能被 n n n 整除的数之间
令:当前能被 n n n 整除的数为 x x x,下一个能被 n n n 整除的数为 y y y
则有,整除分块的区间为 [ ( x + 1 ) ∼ y ] [(x+1) \sim y] [(x+1)∼y]
令: L = x + 1 L=x+1 L=x+1, R = y R=y R=y, v a l u e value value为分块区间的值,则有,
v a l u e = ⌊ n x + 1 ⌋ = ⌊ n L ⌋ value =\left \lfloor \frac{n}{x+1} \right \rfloor=\left \lfloor \frac{n}{L} \right \rfloor value=⌊x+1n⌋=⌊Ln⌋
因为, y y y 能被 n n n 完全整除(PS:余数为 0 0 0)
所以, ⌊ n y ⌋ = n y \left \lfloor \frac{n}{y} \right \rfloor= \frac{n}{y} ⌊yn⌋=yn,且, n y = v a l u e \frac{n}{y}=value yn=value,则有,
n y = v a l u e \frac{n}{y}=value yn=value y = n v a l u e y= \frac{n}{value} y=valuen
将 v a l u e = ⌊ n x + 1 ⌋ value =\left \lfloor \frac{n}{x+1} \right \rfloor value=⌊x+1n⌋ 代入原式得:
y = n ⌊ n x + 1 ⌋ y= \frac{n}{\left \lfloor \frac{n}{x+1} \right \rfloor} y=⌊x+1n⌋n
我们将 L = x + 1 L=x+1 L=x+1, R = y R=y R=y 代入原式得:
R = n ⌊ n L ⌋ R= \frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} R=⌊Ln⌋n
因为
⌊ n L ⌋ = ⌊ n R ⌋ \left \lfloor \frac{n}{L} \right \rfloor=\left \lfloor \frac{n}{R} \right \rfloor ⌊Ln⌋=⌊Rn⌋
且因为 ⌊ n R ⌋ = n R \left \lfloor \frac{n}{R} \right \rfloor= \frac{n}{R} ⌊Rn⌋=Rn
因为 ( n / R ) (n/R) (n/R) 能被 n n n 完全整除
所以可以保证 n n n 能完全整除 ⌊ n L ⌋ \left \lfloor \frac{n}{L} \right \rfloor ⌊Ln⌋
所以我们可以得证:
⌊ n ⌊ n L ⌋ ⌋ = n ⌊ n L ⌋ {\left \lfloor \frac{n}{{\left \lfloor \frac{n}{L} \right \rfloor}} \right \rfloor}= \frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} ⌊⌊Ln⌋n⌋=⌊Ln⌋n
证明完毕
细节详解:
在 i n t , l o n g l o n g int,long long int,longlong 等整数类型中,可以直接进行整除,所以上面的得证等同于 R = ( n / ( n / L ) ) R=(n/(n/L)) R=(n/(n/L))
代码code↓
#include <bits/stdc++.h>
using namespace std;
long long n,L,R,ans=0;
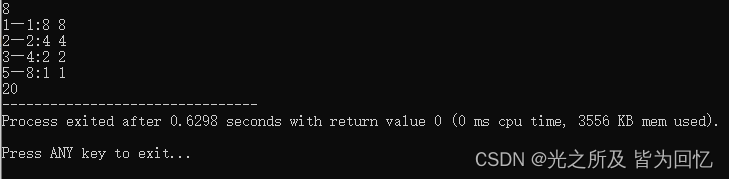
int main(){cin>>n;for(L=1;L<=n;L=R+1){//L=R+1是代表进入下一个块R=n/(n/L);//公式ans+=(R-L+1)*(n/L);//求和cout<<L<<"~"<<R<<":"<<n/R<<" "<<n/L<<endl;//打印分块情况}cout<<ans;//打印和return 0;
}
当 n = 8 n=8 n=8 时的运行结果↓: