【Educoder数据挖掘实训】异常值检测-值域法

开挖！

这个题中$lof$算法给的很抽象，先用比较通俗的方式说一下：
首要想法是找到不合群的点，也就是异常点。采用的方法是对局部可达密度进行判断。相较于其他普通的简单基于聚类的算法，这个算法有两个优点：

1. 可以应对下列问题：
   
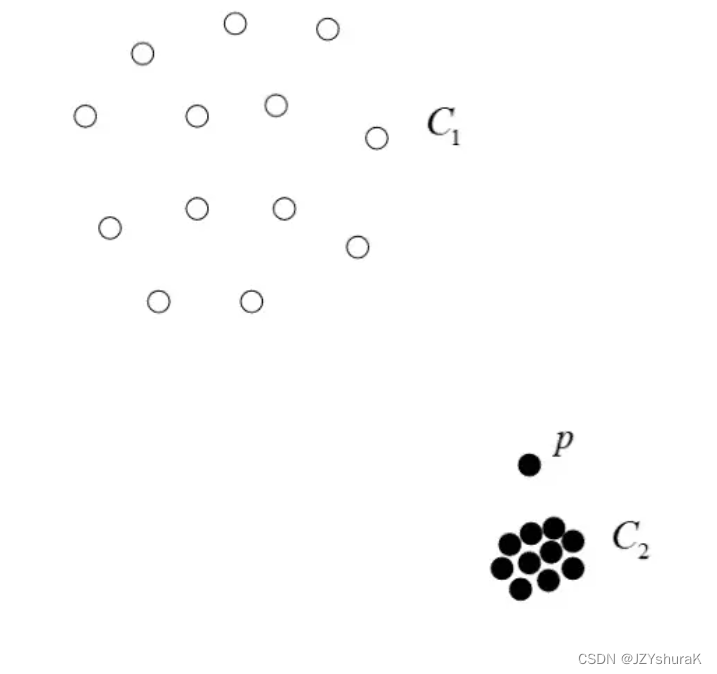
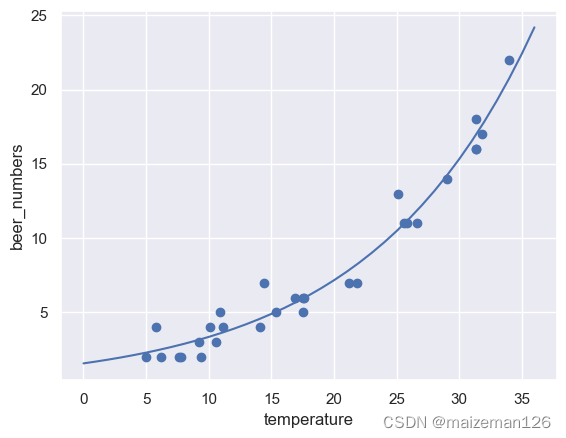
   在上图中，显然$p$是一个异常点。但是可能根据常规的聚类算法很难排除点$p$。原因是点$p$是相较于$C_2$来说的异常点，可是$p$和$C_2$中点的距离和$C_1$中点的平均距离差不多，所以常规的算法无法处理。但是$p$在$lof$算法中密度显然很低，可以被标记出来。
2. 在$lof$算法中，不会像传统异常点检测算法一样直接给出哪些点是异常点，二是会给出每个点的密度。这样可以自己更新阈值更方便后续处理，或者说$lof$算法能更好的处理特殊情况。

那么什么是$lof$算法呢？先定义几个函数：
$d(p,q)$表示点到点的距离；
$d_k(p)$：第$k$距离，表示所有点到$p$的距离里，从小到大排序的第$k$个；
$N_k(p)$：第$k$距离邻域：表示所有点到$p$的距离里，不大于$d_k(p)$的，不难看出$|N_k(p)|\ge k$；
$reach\_dis{t}_k(o,p)=max(d_k(o),d(o,p))$：第$k$可达距离，显然在$o$的第$k$邻域里的点，点$o$到这些点的第$k$可达距离都为第$k$距离。
$lr{d}_k(p)=1/(\frac{{\sum }_{o\in N_k(p)}reach\_dis{t}_k(o,p)}{|N_k(p)|})$：点$p$的第$k$局部可达密度；
$LO{F}_k(p)=\frac{{\sum }_{o\in N_k(p)}\frac{lr{d}_k(o)}{lr{d}_k(p)}}{|N_k(p)|}=\frac{{\sum }_{o\in N_k(p)}lr{d}_k(o)}{|N_k(p)|}/lr{d}_k(p)$：局部离群因子，即将点$p$的$N_k(p)$邻域内所有点的平均局部可达密度与点的局部可达密度做比较，通过这个值来反应点$p$是不是异常点。

所以其实我们要做的就是求出所有点的$LO{F}_k(p)$。
显然有一种做法是$n^3$，即暴力枚举所有点和$k$，这样当然是没问题的。
而且在数据挖掘中往往时间并不占据主要考虑对象，所以时间复杂度显得不是很重要。
但是显然有更优化的方法，比如用$KDTree$来优化这个过程或者$Bal{l}_{T}ree$来优化，效果都是很好的。

---

当然这都不是我们考虑的范围，$Python$已经给出了相应的函数，我们只需要拿来用即可。
但是可能有一个问题，就是上述的$k$到底取多少，题目里也并没有明确强调。经过实验取$10$即可，$Python$函数中默认是$20$。
在求出所有密度之后我们在用$fit\_predict$函数进行预测即可，其中为$-1$的点就是异常点。
代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
# 导入数据
abc = pd.read_csv('deaths.csv')
## 只分析其中的Population和Lat两个变量
abc = abc[["Population","Lat"]]###begin###
lof = LocalOutlierFactor(n_neighbors = 10)
###将lof作用于数据集
score = lof.fit_predict(abc)
ans = 0
for scr in score :if scr == -1 :ans += 1
print("检测出的异常值数量为:", ans)
###end####

一些问题和思考：

1. 首先，这些算法$Python$中都应相应的函数，只需要拿来用即可，关键要考虑清楚输入和输出的格式要求和数据类型。
2. 这里$n\_neighbors=10$并不是强制要求，而是我们采用$fit\_predict$函数进行异常点检测时恰好$k$需要取到$10$，我们如果换一种阈值可能就需要$k$是另一个值。
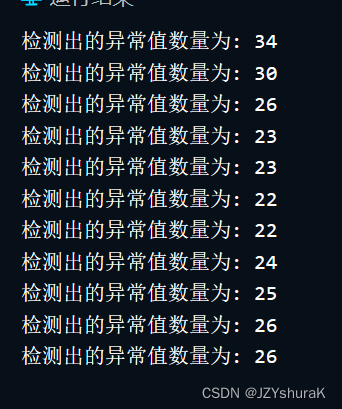
3. 对于$k$值更深层次的理解：这里的$k$并不具备单调属性。很容易被误解成以每个点周围的$k$个点为聚类考虑问题。显然并不是，比如我们将$k$从$10$枚举到$20$，得到的异常点个数并不是单调的：
   这其中的原因是：$k$并不是一个越大越宽松或者越大越严谨的可操控量，$k$只是一个算法中的变量。对于一个未知的数据我们并不能确定$k$的值来找到最好的异常点检测方案。换句话说，对于不同的数据找到最合适的$k$恰恰是我们应用$lof$算法的关键。