参考资料:用python动手学统计学
概率分布为泊松分布、联系函数为对数函数的广义线性模型叫作泊松回归。解释变量可以有多个,连续型和分类型的解释变量也可以同时存在。
1、案例说明
分析不同气温与啤酒销量的关系。构造不同气温下的销量的数学模型,其线性预测算子如下:
如果联系函数为对数函数,则啤酒销量与气温的关系如下:
对两边取指数,变形如下:
2、导入库
# 导入库
# 用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
# 用于估计统计模型的库
import statsmodels.formula.api as smf
import statsmodels.api as sm3、数据准备
beer_num=[ 6, 11, 2, 4, 2, 2, 3, 5, 6, 7, 6, 11, 4, 16, 4, 13, 5, 7, 3, 5, 14, 22, 7, 11, 18, 17, 2, 2, 4, 16]
temp=[17.5, 26.6, 5. , 14.1, 9.4, 7.8, 10.6, 15.4, 16.9, 21.2, 17.6, 25.6, 11.1, 31.3, 5.8, 25.1, 17.5, 21.8, 9.2, 10.9, 29. , 34. , 14.4, 25.8, 31.3, 31.8, 7.6, 6.2, 10.1, 31.3]
beer=pd.DataFrame({'beer_num':beer_num,'temp':temp
})
beer.head()4、泊松回归拟合
mod_pois=smf.glm('beer_num~temp',data=beer,family=sm.families.Poisson()).fit()
mod_pois.summary()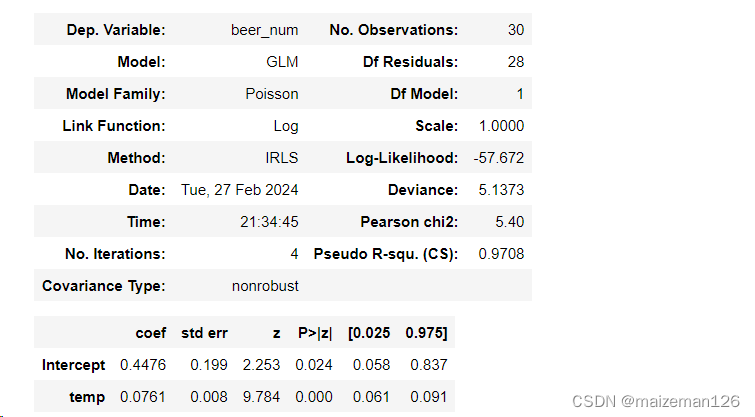
5、模型的选择
# 拟合空模型
mod_pois_null=smf.glm('beer_num~1',data=beer,family=sm.families.Poisson()).fit()
# 输出mod_pois_null和mod_pois的AIC
print('空模型:',mod_pois_null.aic.round(3))
print('气温模型:',mod_pois.aic.round(3))两个模型相比,包含气温变量的模型的AIC更小,说明气温这个解释变量时必要的。
6、回归曲线
seaborn中的函数无法直接绘制出泊松回归的曲线,因而这里把所估计的模型的预测值绘制成散点图。
# 计算预测值
x=np.arange(0,37,1)
pred=mod_pois.predict(pd.DataFrame({'temp':x}))
# 绘制散点图
plt.scatter(x=beer.temp,y=beer.beer_num)
# 绘制预测曲线
plt.plot(x,pred)
# 添加坐标轴标题
plt.xlabel('temperature')
plt.ylabel('beer_numbers')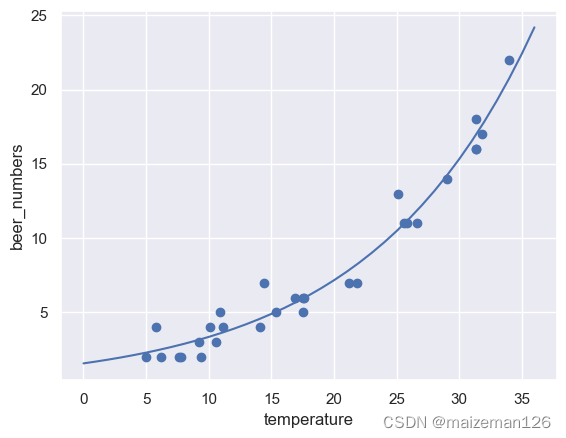
7、泊松回归中回归系数的含义
泊松回归的联系函数为对数函数,对数的一个性质就是把加法变成乘法。在正态线性模型中,回归系数的含义是:x每增加一个单位,y增加系数个单位。而在泊松回归中,x每增加一个单位,y变为原来的多少倍。