DFT应用：计算线性卷积

news/2024/7/27 8:54:01/文章来源:https://blog.csdn.net/qq_40088639/article/details/136549186

目录

一、计算两个有限长序列的线性卷积示例

二、无限长序列和有限长序列的卷积(重叠相加法)

实验1：数据实验

实验2：纯净语音加混响(音效)

二、无限长序列和有限长序列的卷积(重叠保留法)

实验1：数据实验

三、小结

一、计算两个有限长序列的线性卷积示例

FFT计算代码：

baselib.cpp:

#include <stdio.h>
#include <math.h>
#include "common.h"void FFT(double dataR[], double dataI[], double dataA[], int N, int M)
{int i,j,k,r;int p,L,B;unsigned int I,J,K,F0,F1,m,n;double Tr,Ti,temp;//01. 输入序列倒序for(I=0; I<N; I++) {/*获取下标I的反序J的数值*/J=0;for (k=0; k<(M/2+0.5); k++) {m=1; //m是最低位为1的二进制数n=(unsigned int)pow(2,M-1); //n是第M位为1的二进制数m <<= k; //对m左移k位n >>= k; //对n右移k位F0=I & n; //I与n按位与提取出前半部分第k位F1=I & m; //I与m按位与提取出F0对应的后半部分的低位if(F0) J=J | m; //J与m按位或使F0对应低位为1if(F1) J=J | n; //J与n按位或使F1对应高位为1}if (I<J) {//实数部分交换：temp = dataR[I];dataR[I] = dataR[J];dataR[J] = temp;//虚数部分交换temp = dataI[I];dataI[I] = dataI[J];dataI[J] = temp;}}//02. 进行FFT//FFT蝶形级数L从1--Mfor(L=1; L<=M;L++){/*第L级的运算:蝶形运算的种类数目等于间隔B: 有多少种蝶形运算就要需要循环多少次随着循环的不同，旋转指数P也不同，P的增量为k=2^(M-L) *///先计算一下间隔 B = 2^(L-1);B = 1;B = (int)pow(2,L-1);//j = 0,1,2,...,2^(L-1) - 1/*同种蝶形运算*/for (j=0; j<=B-1; j++) {//先计算增量k=2^(M-L)k=1;k = (int)pow(2,M-L);//计算旋转指数p，增量为k时，则P=j*kp=1;p=j*k;/*同种蝶形运算的次数等于增量k=2^(M-L)同种蝶形的运算次数等于蝶形运算的次数*/for (i=0; i<=k-1;i++) {//数组下标定为rr=1;r=j+2*B*i;Tr=dataR[r+B]*cos(2.0*PI*p/N) + dataI[r+B]*sin(2.0*PI*p/N);Ti=dataI[r+B]*cos(2.0*PI*p/N) - dataR[r+B]*sin(2.0*PI*p/N);dataR[r+B]=dataR[r]-Tr;dataI[r+B]=dataI[r]-Ti;dataR[r]=dataR[r]+Tr;dataI[r]=dataI[r]+Ti;}}}//计算幅值if (dataA!=NULL) {for (i=0; i<N; i++) {dataA[i] = sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);}}
}void IFFT(double dataR[], double dataI[], int N, int M)
{int i,j,k,r;int p,L,B;int I,J,K,F0,F1,m,n;double Tr,Ti,temp;//输入序列倒序for(I=0;I< N; I++){/*获取下标I的反序J的数值*/J=0;for (k=0; k<(M/2+0.5); k++) {m=1;//m是最低位为1的二进制数n=(unsigned int)pow(2,M-1);//n是第M位为1的二进制数m <<= k; //对m左移k位n >>= k; //对n右移k位F0=I & n;//I与n按位与提取出前半部分第k位F1=I & m;//I与m按位与提取出F0对应的后半部分的低位if(F0) J=J | m; //J与m按位或使F0对应低位为1if(F1) J=J | n; //J与n按位或使F1对应高位为1}if (I<J) {temp = dataR[I];dataR[I] = dataR[J];dataR[J] = temp;temp = dataI[I];dataI[I] = dataI[J];dataI[J] = temp;}}//进行IFFT//FFT蝶形级数L从1--Mfor (L=1; L<=M; L++){/*第L级的运算:蝶形运算的种类数目等于间隔B: 有多少种蝶形运算就要需要循环多少次随着循环的不同，旋转指数P也不同，P的增量为k=2^(M-L)*///先计算一下间隔 B = 2^(L-1);B = 1;B = (int)pow(2,L-1);//j = 0,1,2,...,2^(L-1) - 1for (j=0; j<=B-1; j++){	/*同种蝶形运算*///先计算增量k=2^(M-L)k=1;k = (int)pow(2,M-L);//计算旋转指数p，增量为k时，则P=j*kp=1;p=j*k;/*同种蝶形运算的次数等于增量k=2^(M-L)；同种蝶形的运算次数等于蝶形运算的次数*/for (i=0; i<=k-1; i++) {//数组下标定为rr=1;r=j+2*B*i;Tr=dataR[r+B]*cos(2.0*PI*p/N) - dataI[r+B]*sin(2.0*PI*p/N);Ti=dataI[r+B]*cos(2.0*PI*p/N) + dataR[r+B]*sin(2.0*PI*p/N);dataR[r+B]=dataR[r]-Tr;dataR[r+B]=dataR[r+B]/2;dataI[r+B]=dataI[r]-Ti;dataI[r+B]=dataI[r+B]/2;dataR[r]=dataR[r]+Tr;dataR[r]=dataR[r]/2;dataI[r]=dataI[r]+Ti;dataI[r]=dataI[r]/2;}}}
}

baselib.h：

#ifndef __BASIC_LIB_H__
#define __BASIC_LIB_H__
#include "common.h"void FFT(double dataR[], double dataI[], double dataA[], int N, int M);
void IFFT(double dataR[], double dataI[], int N, int M);#endif /* __BASIC_LIB_H__ */

common.h：

#ifndef  __TYPEDEFS_H_
#define  __TYPEDEFS_H_#define PI (3.141592653589793)typedef struct {double real;double img;
}complex;#endif  //__TYPEDEFS_H_

main.c：

#define _FFT_LEN (16)
#define _FFT_ORDER 4#define SEQ1_LEN 8
#define SEQ2_LEN 5
int main(void)
{int i;//8+5-1=12<16[FFT的长度]double input_seq1[SEQ1_LEN]={1,2,3,4,5,4,3,2};double input_seq2[SEQ2_LEN]={1,1,1,1,1};double *res_seq_r=(double *)calloc(_FFT_LEN, sizeof(double));double *res_seq_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_i=(double *)calloc(_FFT_LEN, sizeof(double));//init input sequencefor(i=0; i< SEQ1_LEN; i++) {xn1_r[i]=input_seq1[i];}for(i=0; i< SEQ2_LEN; i++) {xn2_r[i]=input_seq2[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor(i=0; i<_FFT_LEN; i++){res_seq_r[i]=xn1_r[i]*xn2_r[i] - xn1_i[i]*xn2_i[i];res_seq_i[i] =xn1_r[i]*xn2_i[i] + xn1_i[i]*xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);for (i=0; i<SEQ1_LEN+SEQ2_LEN-1; i++) {printf("%f ", res_seq_r[i]);}printf("\n");
}

结果：

1.000000 3.000000 6.000000 10.000000 15.000000 18.000000 19.000000 18.000000 14.000000 9.000000 5.000000 2.000000

要注意的两个点：（1）圆周卷积的长度就是FFT的点数(2的整数倍次幂)；（2）圆周卷积长度和线性卷积长度的关系。

二、无限长序列和有限长序列的卷积(重叠相加法)

实验1：数据实验

给出x(n)={1,2,3,4,5, 1,2,3,4,5, 1,2,3,4,5, …},0≤n≤29; h(n)={1,2,1}; 0≤n≤2; 求y(n)=x(n)*h(n)。

对比：先直接进行计算，代码如下：

main.c：

#define _FFT_LEN (32)
#define _FFT_ORDER 5#define SEQ1_LEN 30
#define SEQ2_LEN 3
int main(void)
{int i;//30+3-1=32<=32[FFT的长度]double input_seq1[SEQ1_LEN]={1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5};double input_seq2[SEQ2_LEN]={1,2,1};double *res_seq_r=(double *)calloc(_FFT_LEN, sizeof(double));double *res_seq_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_i=(double *)calloc(_FFT_LEN, sizeof(double));//init input sequencefor(i=0; i< SEQ1_LEN; i++) {xn1_r[i]=input_seq1[i];}for(i=0; i< SEQ2_LEN; i++) {xn2_r[i]=input_seq2[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor(i=0; i<_FFT_LEN; i++){res_seq_r[i]=xn1_r[i]*xn2_r[i] - xn1_i[i]*xn2_i[i];res_seq_i[i] =xn1_r[i]*xn2_i[i] + xn1_i[i]*xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);for (i=0; i<SEQ1_LEN+SEQ2_LEN-1; i++) {printf("%f ", res_seq_r[i]);}printf("\n");
}

结果如下：

1.000000 4.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 14.000000 5.000000

利用重叠相加法(长序列进行均匀分段)，短序列长度M=3，长序列分段后N=5，则计算如下：

#define _FFT_LEN (8)
#define _FFT_ORDER 3#define SEQ1_LEN 30
#define SEQ2_LEN 3//重叠相加法
#define M SEQ2_LEN
#define N 5 /* 长序列均匀分段的每一段长度 */int main(void)
{int i, j, k;double *res_seq_r=(double *)calloc(_FFT_LEN, sizeof(double));double *res_seq_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_i=(double *)calloc(_FFT_LEN, sizeof(double));//30+3-1=32<=32[FFT的长度]double input_seq1[SEQ1_LEN]={1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5};
//	double input_seq1[SEQ1_LEN];
//	for(i=0; i<30; i++)
//		input_seq1[i]=i;double input_seq2[SEQ2_LEN]={1,2,1};double xk[N];double overlap[M-1];for(k=2; k<SEQ1_LEN/N; k++) {memset(xn1_r, 0, _FFT_LEN*sizeof(double));memset(xn1_i, 0, _FFT_LEN*sizeof(double));memset(xn2_r, 0, _FFT_LEN*sizeof(double));memset(xn2_i, 0, _FFT_LEN*sizeof(double));memset(res_seq_r, 0, _FFT_LEN*sizeof(double));memset(res_seq_i, 0, _FFT_LEN*sizeof(double));for(j=0; j<N; j++) {xk[j]=input_seq1[k*N+j];}//init input sequencefor(i=0; i< N; i++) {xn1_r[i]=xk[i];}//5+3-1=7,所以每小段做8个点的FFT即可。for(i=0; i< M; i++) {xn2_r[i]=input_seq2[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor(i=0; i<_FFT_LEN; i++){res_seq_r[i]=xn1_r[i]*xn2_r[i] - xn1_i[i]*xn2_i[i];res_seq_i[i]=xn1_r[i]*xn2_i[i] + xn1_i[i]*xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);for (i=0; i<N+M-1; i++) {printf("%f ", res_seq_r[i]);}printf("\n");}
}

结果：重叠的点有M-1个，长序列的长度为N，线性卷积后，结果长度为N+(M-1)，M-1就是多出来的重叠的点。

1.000000 4.000000 8.000000 12.000000 16.000000 14.000000 5.000000 

1.000000 4.000000 8.000000 12.000000 16.000000 14.000000 5.000000

1.000000 4.000000 8.000000 12.000000 16.000000 14.000000 5.000000

1.000000 4.000000 8.000000 12.000000 16.000000 14.000000 5.000000

接下来处理重叠的部分(相加)：

#define _FFT_LEN (8)
#define _FFT_ORDER 3#define SEQ1_LEN 30
#define SEQ2_LEN 3//重叠相加法
#define M SEQ2_LEN
#define N 5 /* 长序列均匀分段的每一段长度 */int main(void)
{int i, j, k;double *res_seq_r=(double *)calloc(_FFT_LEN, sizeof(double));double *res_seq_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_i=(double *)calloc(_FFT_LEN, sizeof(double));//30+3-1=32<=32[FFT的长度]double input_seq[SEQ1_LEN]={1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5};double output_seq[SEQ1_LEN+SEQ2_LEN-1];//	double input_seq1[SEQ1_LEN];
//	for(i=0; i<30; i++)
//		input_seq1[i]=i;double input_seq2[SEQ2_LEN]={1,2,1};double xk[N];double overlap[M-1];memset(overlap, 0, (M-1)*sizeof(double));for(k=0; k<SEQ1_LEN/N; k++){memset(xn1_r, 0, _FFT_LEN*sizeof(double));memset(xn1_i, 0, _FFT_LEN*sizeof(double));memset(xn2_r, 0, _FFT_LEN*sizeof(double));memset(xn2_i, 0, _FFT_LEN*sizeof(double));memset(res_seq_r, 0, _FFT_LEN*sizeof(double));memset(res_seq_i, 0, _FFT_LEN*sizeof(double));for(j=0; j<N; j++) {xk[j]=input_seq[k*N+j];}//init input sequencefor(i=0; i< N; i++) {xn1_r[i]=xk[i];}//5+3-1=7,所以每小段做8个点的FFT即可。for(i=0; i< M; i++) {xn2_r[i]=input_seq2[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor(i=0; i<_FFT_LEN; i++){res_seq_r[i]=xn1_r[i]*xn2_r[i] - xn1_i[i]*xn2_i[i];res_seq_i[i]=xn1_r[i]*xn2_i[i] + xn1_i[i]*xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);//overlap addfor(i=0; i<M-1; i++) {res_seq_r[i]=overlap[i]+res_seq_r[i];overlap[i]=res_seq_r[i+N];}if(k!=SEQ1_LEN/N-1){for (i=0; i<N; i++) {output_seq[k*N+i]=res_seq_r[i];printf("%f ", output_seq[k*N+i]);}} else {for (i=0; i<N+M-1; i++)output_seq[k*N+i]=res_seq_r[i];}}for (i=0; i<SEQ1_LEN+SEQ2_LEN-1; i++) {printf("%f ", output_seq[i]);}printf("\n");
}

结果：分段计算和整体直接计算的结果是一样的

1.000000 4.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 15.000000 9.000000 8.000000 12.000000 16.000000 14.000000 5.000000

实验2：纯净语音加混响(音效)

给出短序列(有限长序列)为房间冲击响应，长序列是一段纯净语音序列。

分析：纯净语音序列长度是72000，房间冲击响应是4096个点。短序列长度M=4096，长序列均匀分段的每段长度定义为N=4097，那对于每一段来说：线性卷积的长度就是N+M-1=8192，选取圆周卷积的长度为8192(同时也是FFT的长度)，那圆周卷积的结果就是线性卷积的结果(通过圆周卷积来计算线性卷积)。如下图：

代码：

main.c

void conv_overlap(double *long_seq, int long_seq_len, double *short_seq, int short_seq_len, double *outputdata);int main(void)
{int count, i=0;//open input and output fileFILE *fpin, *fpout;fpin=fopen("audio.raw", "rb");if (NULL == fpin) {printf("open source file error!\n");fclose(fpin);return -1;}fpout=fopen("audio_out.raw", "wb");if (NULL == fpin) {printf("open output file error!\n");fclose(fpin);fclose(fpout);return -1;}//get date length of input audio file//Note：没有处理wav格式文件的文件头fseek(fpin, 0, SEEK_END);int rir_length = sizeof(rir)/sizeof(double);//4096int inputdata_length=ftell(fpin);inputdata_length = inputdata_length/2;printf("len of rir:%d\n", rir_length);//4096printf("input voice length:%d\n", inputdata_length);//72000rewind(fpin);short *inputdata = (short *)malloc(inputdata_length * sizeof(short));short *outputdata = (short *)malloc((inputdata_length+rir_length-1) * sizeof(short));count = fread(inputdata, sizeof(short), inputdata_length, fpin);//add rirconv_overlap_voice(inputdata, inputdata_length, rir, rir_length, outputdata);//save outputfwrite(outputdata, sizeof(short), inputdata_length, fpout);free(inputdata);free(outputdata);fclose(fpin);fclose(fpout);return 0;
}#define _FFT_LEN (8192)
#define _FFT_ORDER 13//重叠相加法
#define M 4096
#define N 4097 /* 长序列均匀分段的每一段长度 */void conv_overlap_voice(short *long_seq, long long_seq_len, double *short_seq, long short_seq_len, short *outputdata)
{int i, j, k;double *res_seq_r=(double *)calloc(_FFT_LEN, sizeof(double));double *res_seq_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn1_i=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_r=(double *)calloc(_FFT_LEN, sizeof(double));double *xn2_i=(double *)calloc(_FFT_LEN, sizeof(double));short *long_seq_ptr=long_seq;short *outputdata_ptr=outputdata;/* 4096+4097-1=8192<=8192[FFT的长度] */
//	SEQ1_LEN=long_seq_len;
//	SEQ2_LEN=short_seq_len;
//	input_seq=long_seq;
//	input_seq2=short_seq;double xk[N];double overlap[M-1];memset(overlap, 0, (M-1)*sizeof(double));for(k=0; k<long_seq_len/N; k++){memset(xn1_r, 0, _FFT_LEN*sizeof(double));memset(xn1_i, 0, _FFT_LEN*sizeof(double));memset(xn2_r, 0, _FFT_LEN*sizeof(double));memset(xn2_i, 0, _FFT_LEN*sizeof(double));memset(res_seq_r, 0, _FFT_LEN*sizeof(double));memset(res_seq_i, 0, _FFT_LEN*sizeof(double));for(j=0; j<N; j++) {xk[j]=(double)(long_seq_ptr[k*N+j]/32767.0);}//init input sequencefor(i=0; i< N; i++) {xn1_r[i]=xk[i];}for(i=0; i< M; i++) {xn2_r[i]=short_seq[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor(i=0; i<_FFT_LEN; i++){res_seq_r[i]=xn1_r[i]*xn2_r[i] - xn1_i[i]*xn2_i[i];res_seq_i[i]=xn1_r[i]*xn2_i[i] + xn1_i[i]*xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);//overlap addfor(i=0; i<M-1; i++) {res_seq_r[i]=overlap[i]+res_seq_r[i];overlap[i]=res_seq_r[i+N];}if(k!=long_seq_len/N-1){for (i=0; i<N; i++) {outputdata_ptr[k*N+i]=(short)(res_seq_r[i]*32767.0);//printf("%f ", output_seq[k*N+i]);}} else { //最后一段for (i=0; i<N+M-1; i++)outputdata_ptr[k*N+i]=(short)(res_seq_r[i]*32767.0);}}//	for (i=0; i<long_seq_len+short_seq_len-1; i++) {
//			printf("%f ", outputdata[i]);
//	}
//	printf("\n");free(xn1_r);free(xn1_i);free(xn2_r);free(xn2_i);free(res_seq_r);free(res_seq_i);printf("process done\n");
}

运行结果对比：

原纯净语音

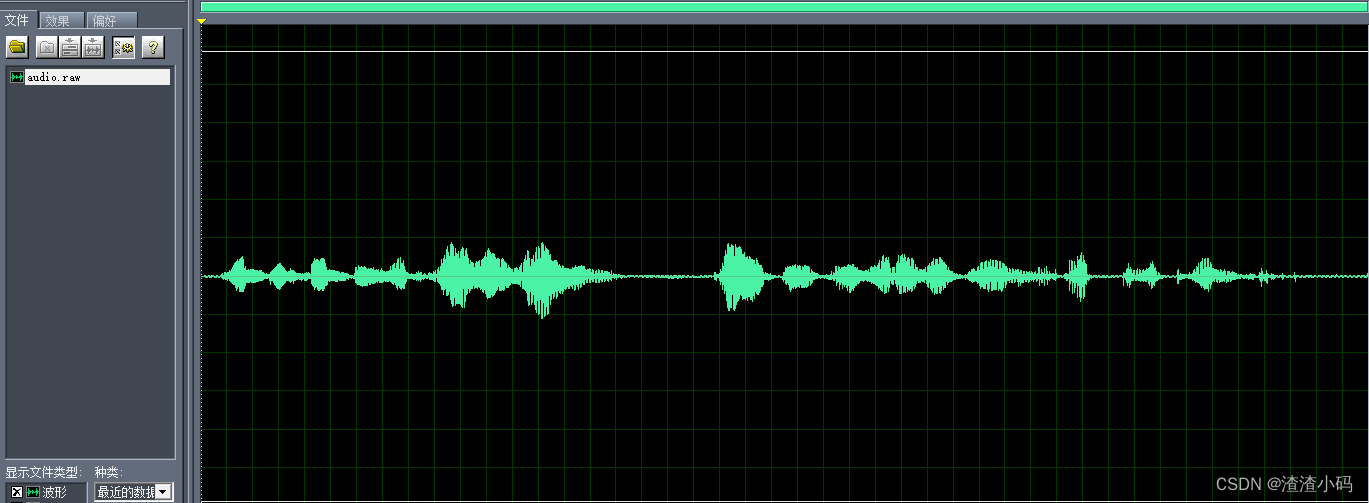加了混响后：

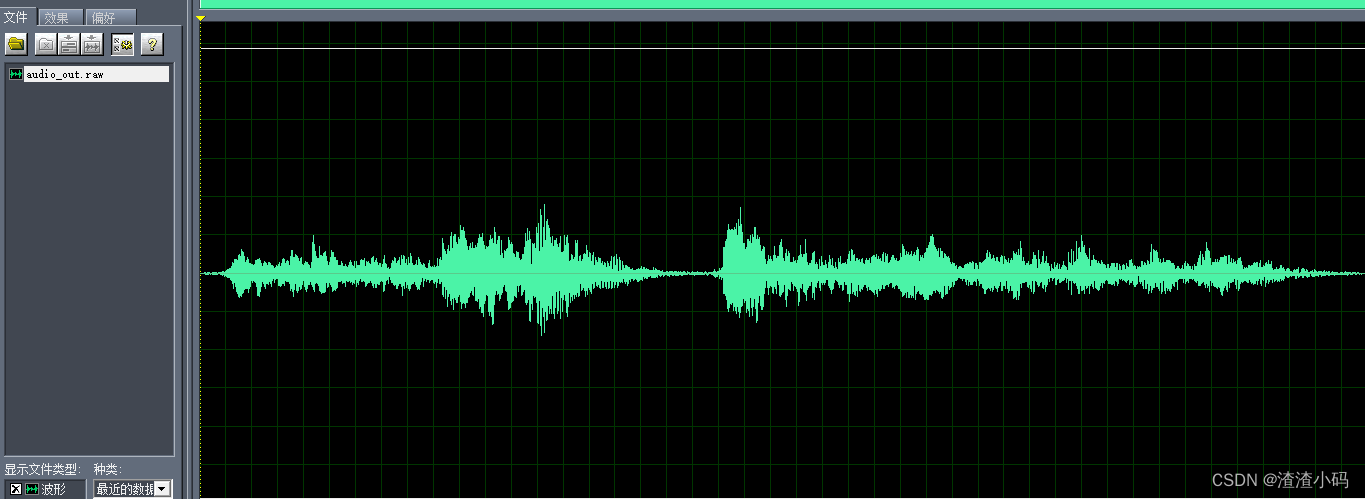
二、无限长序列和有限长序列的卷积(重叠保留法)

实验1：数据实验

给出x(n)={1,2,3,4,5, 1,2,3,4,5, 1,2,3,4,5, …},0≤n≤29; h(n)={1,2,1}; 0≤n≤2; 利用重叠保留法计算y(n)=x(n)*h(n)。

main.c：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#include "common.h"
#include "baselib.h"#define _FFT_LEN (8)
#define _FFT_ORDER 3#define SEQ1_LEN 30
#define SEQ2_LEN 3//重叠相加法
#define M SEQ2_LEN
#define N 5 /* 长序列均匀分段的每一段长度 */int main(void)
{int i, j, k;double* res_seq_r = (double*)calloc(_FFT_LEN, sizeof(double));double* res_seq_i = (double*)calloc(_FFT_LEN, sizeof(double));double* xn1_r = (double*)calloc(_FFT_LEN, sizeof(double));double* xn1_i = (double*)calloc(_FFT_LEN, sizeof(double));double* xn2_r = (double*)calloc(_FFT_LEN, sizeof(double));double* xn2_i = (double*)calloc(_FFT_LEN, sizeof(double));double input_seq[SEQ1_LEN] = { 1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5 };double input_seq2[SEQ2_LEN] = { 1,2,1 };double output_seq[SEQ1_LEN];double xk[M-1+N]; //输入的子序列的长(参与圆周卷积)double overlap[M - 1];memset(overlap, 0, (M - 1) * sizeof(double));for (k = 0; k <=SEQ1_LEN / N; k++){memset(xn1_r, 0, _FFT_LEN * sizeof(double));memset(xn1_i, 0, _FFT_LEN * sizeof(double));memset(xn2_r, 0, _FFT_LEN * sizeof(double));memset(xn2_i, 0, _FFT_LEN * sizeof(double));memset(res_seq_r, 0, _FFT_LEN * sizeof(double));memset(res_seq_i, 0, _FFT_LEN * sizeof(double));memset(xk, 0, (M-1+N) * sizeof(double));if(k==0) { //第一个子段for (j = 0; j < N; j++)xk[j+M-1] = input_seq[k * N + j];} else if(k == SEQ1_LEN / N){ //最后一个子段for(i=0;i<M-1;i++)xk[i]=input_seq[SEQ1_LEN-M+1+i];for (j = 0; j < N; j++)xk[j+M-1]=0;} else {for (i = 0; i < M - 1; i++)xk[i] = input_seq[k*N - M + 1+i];//3 4for (i = 0; i <N; i++)xk[i+M-1] = input_seq[k*N+i];}//for (i = 0; i < M - 1 + N; i++) {//printf("%f ", xk[i]);//}//printf("\n");//init input sequence(len=M-1+N)for (i = 0; i < M-1+N; i++) {//补一个0，达到FFT的长度8xn1_r[i] = xk[i];}//补5个0，达到FFT的长度for (i = 0; i < M; i++) {xn2_r[i] = input_seq2[i];}FFT(xn1_r, xn1_i, NULL, _FFT_LEN, _FFT_ORDER);FFT(xn2_r, xn2_i, NULL, _FFT_LEN, _FFT_ORDER);//Multiplication in frequency domainfor (i = 0; i < _FFT_LEN; i++) {res_seq_r[i] = xn1_r[i] * xn2_r[i] - xn1_i[i] * xn2_i[i];res_seq_i[i] = xn1_r[i] * xn2_i[i] + xn1_i[i] * xn2_r[i];}//iFFTIFFT(res_seq_r, res_seq_i, _FFT_LEN, _FFT_ORDER);//舍掉输出序列的前M-1个点后，连续取N个点，后面的点舍掉//后面的点是因为FFT的长度大于圆周卷积的长度M-1+N而计算出来的for (i = M-1; i < M-1+N; i++) {//for (i = 0; i < _FFT_LEN; i++) {printf("%f ", res_seq_r[i]);}printf("\n");//break;}
}

结果：

1.000000 4.000000 8.000000 12.000000 16.000000

15.000000 9.000000 8.000000 12.000000 16.000000

15.000000 9.000000 8.000000 12.000000 16.000000

15.000000 9.000000 8.000000 12.000000 16.000000

15.000000 9.000000 8.000000 12.000000 16.000000

15.000000 9.000000 8.000000 12.000000 16.000000

14.000000 5.000000 0.000000 0.000000 0.000000

三、小结

1. 以上测试代码只是理论公式的验证，仿真用的

2. 可以优化的点：比如短序列一般是提前知道的，可以事先计算其FFT，减少实时运算过程的运算量；代码流程上的优化；空间数据buffer的优化；FFT算法的优化；或者可以转为定点运算...。

3. 注意对比两种算法：分段有无重叠，输出结果有无重叠；均匀分段如何取值，线性卷积、循环卷积、FFT等几个长度间的关系。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.luyixian.cn/news_show_997518.aspx

如若内容造成侵权/违法违规/事实不符，请联系dt猫网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

[⑥5G NR]: 无线接口协议，信道映射学习

[⑥5G NR]: 无线接口协议，信道映射学习

5G系统整体包括核心网、接入网以及终端部分&#xff0c;接入网与终端间通过无线空口协议栈进行连接。无线接口可分为三个协议层&#xff1a;物理层&#xff08;L1&#xff09;、数据链路层&#xff08;L2&#xff09;和网络层&#xff08;L3&#xff09;。 L1&#xff1a;物理…
阅读更多...
利用OpenCV 抽取视频的图片，并制作目标检测数据集

利用OpenCV 抽取视频的图片，并制作目标检测数据集

1、前言 目标检测中&#xff0c;图片的数据可以从视频中抽取&#xff0c;而OpenCV的VideoCapture可以实现这样的操作 需要的库文件 opencv pip下载&#xff1a; pip install opencv-contrib-python 更换镜像源下载&#xff1a; pip install opencv-contrib-python -i htt…
阅读更多...
Linux 理解操作系统

Linux 理解操作系统

目录 一、冯诺依曼体系结构 二、操作系统 1、概念 2、设计OS的目的 3、定位 4、先描述再组织 5、系统调用和库函数概念 一、冯诺依曼体系结构 计算机&#xff0c;都是有一个个的硬件组件组成&#xff1a; 输入单元&#xff1a;包括键盘, 鼠标&#xff0c;扫描仪, 写板等…
阅读更多...
寻找旋转排序数组中的最小值[中等]

寻找旋转排序数组中的最小值[中等]

优质博文IT-BLOG-CN 一、题目 已知一个长度为n的数组&#xff0c;预先按照升序排列&#xff0c;经由1到n次 旋转 后&#xff0c;得到输入数组。例如&#xff0c;原数组nums [0,1,2,4,5,6,7]在变化后可能得到&#xff1a; 【1】若旋转4次&#xff0c;则可以得到[4,5,6,7,0,1,2…
阅读更多...
Flink ExecuteGraph构建源码解析

Flink ExecuteGraph构建源码解析

文章目录 前言ExecutionGraph中的主要抽象概念源码核心代码入口源码核心流程&#xff1a; 前言 在JobGraph构建过程中分析了JobGraph的构建过程&#xff0c;本文分析ExecutionGraph的构建过程。JobManager(JobMaster) 根据 JobGraph 生成 ExecutionGraph。ExecutionGraph是JobG…
阅读更多...
C++前置声明的学习

C++前置声明的学习

【C】C中前置声明的应用与陷阱_前置生命如何使用-CSDN博客 首先&#xff0c;这样写会报错&#xff1a; #pragma once #include "A.h" class B {A a; public:B(void);~B(void); };#include "B.h" B::B(void) { }B::~B(void) { } #pragma once #include &…
阅读更多...
URL?后参数有特殊字符问题

URL?后参数有特殊字符问题

前端对于URL的参数不做处理 不处理、用URLDecoder.decode()处理、用URLEncoder.encode()处理、用URLEncoder.encode()处理后再用URLDecoder.decode()处理 结果 前端对于URL的参数用encodeURIComponent(‘XF-OPPZZD-26*316’)处理 结果 前端不处理有&字符时 结果会把后…
阅读更多...
前端网络请求异步处理——Promise使用记录

前端网络请求异步处理——Promise使用记录

Promise是ES6中新增的一个处理复杂异步请求的工具&#xff0c;其主要形式为&#xff1a; const baseUrl http://localhost:80 export const $request (param {}) > {console.log(请求参数, param)return new Promise((resolve, reject) > {wx.request({url: baseUrl …
阅读更多...
海外服务器被DDOS攻击了该怎么办

海外服务器被DDOS攻击了该怎么办

在当今全球化的时代&#xff0c;越来越多的企业和组织选择将业务拓展至海外市场。然而&#xff0c;随着业务的扩大和网络的延伸&#xff0c;也面临着来自不同地区的网络威胁和攻击风险。如果您的海外服务器遭受了DDOS攻击&#xff0c;以下是一些应对措施&#xff1a; 一、立即断…
阅读更多...
【Redis】Redis的应用场景

【Redis】Redis的应用场景

&#x1f4dd;个人主页&#xff1a;五敷有你 &#x1f525;系列专栏&#xff1a;Redis ⛺️稳中求进&#xff0c;晒太阳 Redis的应用场景&#xff1a; 限流 要求10s内只能访问一次 RequestMapping("xian")public String xianLiu(String sign){String sign1 …
阅读更多...
力扣刷题

力扣刷题

文章目录 1. 双指针1.1 两数之和1.2 三数之和1.3 盛最多水的容器1.4 接雨水 2. 字串2.1 滑动窗口最大值 3. 动态规划4. 多维动态规划4.1 最长回文字串 1. 双指针 1.1 两数之和 思路&#xff1a;因为是有序数组&#xff0c; 1.2 三数之和 题目要求不能重复 思路&#xff1a;三…
阅读更多...
简明固体物理--晶体的形成与晶体结构的描述

简明固体物理--晶体的形成与晶体结构的描述

简明固体物理-国防科技大学 chapter 1 Formation of Crystal Contents and roadmapQuantum Mechanics and atomic structureElectronsOld quantum theoryMethod of Quantum MechanicsDistributing functions of micro-particles BindingCrystal structure and typical crystal…
阅读更多...
YOLOv9(2):YOLOv9网络结构

YOLOv9(2):YOLOv9网络结构

1. 前言 本文仅以官方提供的yolov9.yaml来进行简要讲解。 讲解之前&#xff0c;还是要做一些简单的铺垫。 Slice层不做任何的操作&#xff0c;纯粹是做一个占位层。这样一来&#xff0c;在parse_model时&#xff0c;ch[n]可表示第n层的输出通道。 Detect和DDetect主要区别还…
阅读更多...
Java开发从入门到精通（一）：Java的基础语法进阶

Java开发从入门到精通（一）：Java的基础语法进阶

Java大数据开发和安全开发 &#xff08;一&#xff09;Java注释符1.1 单行注释 //1.2 多行注释 /* */1.3 文档注释 /** */1.4 各种注释区别1.5 注释的特点1.5 注释的快捷键 &#xff08;二&#xff09;Java的字面量&#xff08;三&#xff09;Java的变量3.1 认识变量3.2 为什么…
阅读更多...
例行性工作(at,crontab)

例行性工作(at,crontab)

目录 单一执行的例行性工作at 语法 选项 时间格式 at的工作文件存放目录 at工作的日志文件 实例 命令总结&#xff1a; 循环执行的例行性工作crond 语法 选项 crontab工作调度对应的系统服务 crontab工作的日志文件 用户定义计划任务的文件所在目录 动态查看 crontab文件格式 文…
阅读更多...
集合拆分Lists.partition的使用

集合拆分Lists.partition的使用

集合拆分Lists.partition的使用 集合拆分Lists.partition的使用 需要的包 import com.google.common.collect.Lists;引入maven依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>21.0</…
阅读更多...
真Unity-Editor二次开发-ScriptableObject 可自定义UI界面

真Unity-Editor二次开发-ScriptableObject 可自定义UI界面

关于ScriptablObject自定义 作为官方指定的&#xff0c;曾经我也吐槽过ScriptableObject很鸡肋&#xff0c;个人曾经也是强烈反对在项目中使用&#xff0c;但直到我今天看到下面这个代码&#xff0c;菜发现其实只是自己太菜鸡而已 --------------不想多写什么 -------------…
阅读更多...
Rust组织管理，箱Crate包Package和模块module定义和区别，use关键字作用

Rust组织管理，箱Crate包Package和模块module定义和区别，use关键字作用

Rust 组织管理 任何一门编程语言如果不能组织代码都是难以深入的&#xff0c;几乎没有一个软件产品是由一个源文件编译而成的。 本教程到目前为止所有的程序都是在一个文件中编写的&#xff0c;主要是为了方便学习 Rust 语言的语法和概念。 对于一个工程来讲&#xff0c;组织…
阅读更多...
NineData与OceanBase完成产品兼容认证，共筑企业级数据库新生态

NineData与OceanBase完成产品兼容认证，共筑企业级数据库新生态

近日&#xff0c;云原生智能数据管理平台 NineData 和北京奥星贝斯科技有限公司的 OceanBase 数据库完成产品兼容互认证。经过严格的联合测试&#xff0c;双方软件完全相互兼容、功能完善、整体运行稳定且性能表现优异。 此次 NineData 与 OceanBase 完成产品兼容认证&#xf…
阅读更多...
Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页

Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页

Manz高压清洗机S11-028GCH-High Quality Cleaner 操作使用说明492页
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023

友情链接： 我的编程经验分享 一条长河网 尧图网站开发 尧图建网站 广利置业