一、leetcode 91解码方法
1、题目解析

这道题就是需要我们对一个数组进行解码,返回有多少种方法就行了。
但是有几个特殊情况:06 不可以为一组、60 也不可以、6 、0也不行
2、算法原理
a状态表示
根据经验+题目要求确定表示方程
以i位置为结尾,。。。。或者以i位置开始,。。。。
表示方程:dp[i] 从0开始到i位置的解码方法总数
b状态转移方程
根据最近的一步划分问题
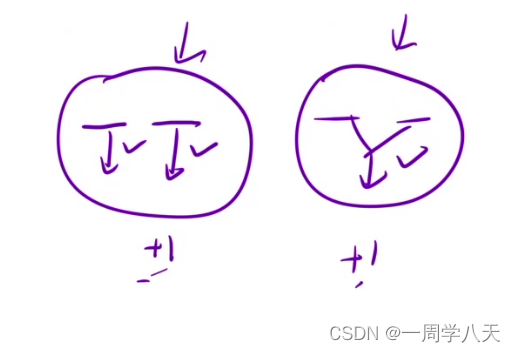
i位置单独解码或者 与i-1合并解码

状态转移方程:dp[i]=dp[i-1]+dp[i-2],成功的情况相加
c初始化

dp[1]有两种情况,与dp[0]单独解码或者合并解码
d填表顺序
从左往右
e返回值
dp[n-1]
3、代码
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int > dp(n);//初始化if('1'<=s[0]&&s[0]<='9') dp[0]=1;else dp[0]=0;//dp[0]=s[0]!='0';//处理边界情况if(s.size()==1){return dp[0];}if(s[1]!='0') dp[1]+=dp[0];int t=(s[0]-'0')*10+s[1]-'0';if(10<=t&&t<=26)dp[1]+=1;//填表for(int i=2;i<n;i++){if(s[i]!='0') dp[i]+=dp[i-1];int t=(s[i-1]-'0')*10+s[i]-'0';if(10<=t&&t<=26)dp[i]+=dp[i-2];}return dp[n-1];}
};o(n)
优化
处理边界问题以及初始化问题技巧
添加一个虚拟节点
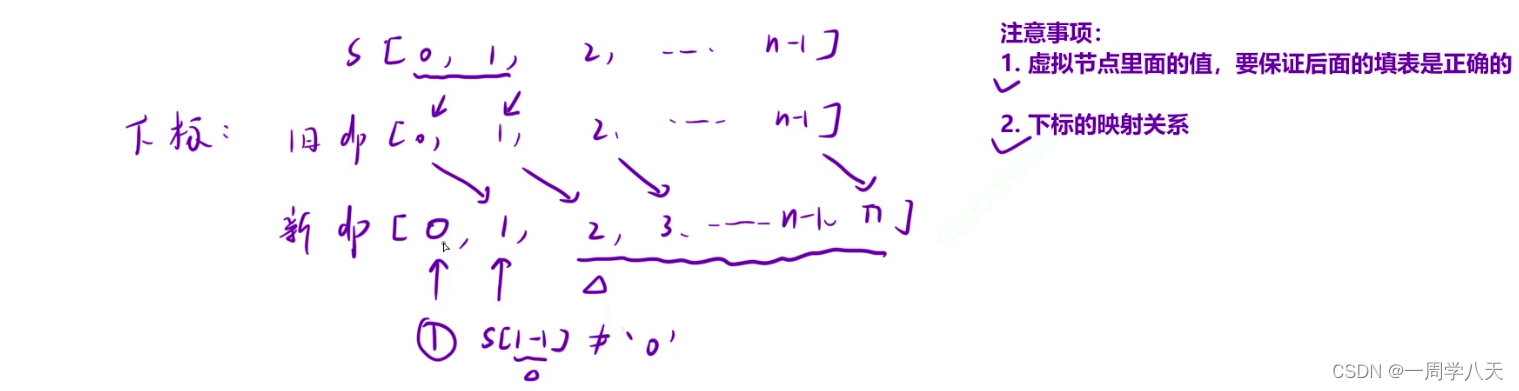
虚拟节点如何设值——抱枕后续填表时正确的,就比如新表ndp[2]和ndp[1]可以合并,为了保证期准确度我们给ndp[0]设值为1.
需要注意的映射关系,ndp下标-1才是对一的s下标,
优化后代码:
class Solution
{
public:int numDecodings(string s){// 优化int n = s.size();vector<int> dp(n + 1); dp[0] = 1; // 保证后续填表是正确的dp[1] = s[0] != '0';// 填表for (int i = 2; i <= n; i++){// 处理单独编码if (s[i - 1] != '0') dp[i] += dp[i - 1];// 如果和前⾯的⼀个数联合起来编码int t = (s[i - 2] - '0') * 10 + s[i - 1] - '0';if (t >= 10 && t <= 26) dp[i] += dp[i - 2];}return dp[n];}
};二、62不同路径
1、题目解析

机器人只能向下或者向上移动
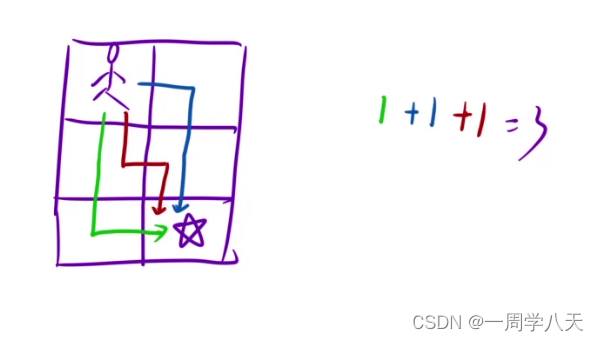
2、算法原理
a状态表示
经验+题目要求
以[i][j]为结尾+

b状态转移方程
最近的一步。划分问题
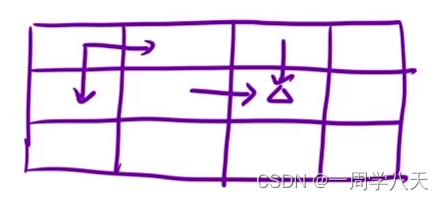
要么从上面要么从左边来
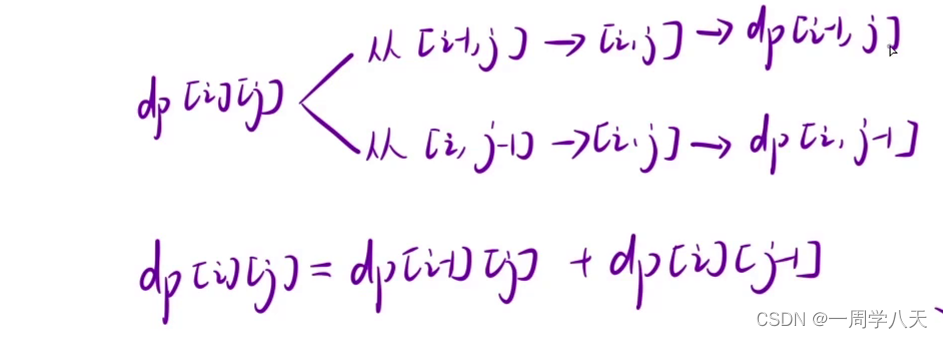
c初始化
与第一题类似,为了避开繁琐的初始化行为,第一题是一维数组添加一个节点即可,
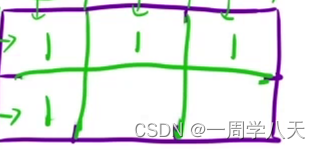
二维数组我们需要初始化的值是第一行和第一列为了避免越界问题。我们可以与第一题类似的方式设置虚拟节点。
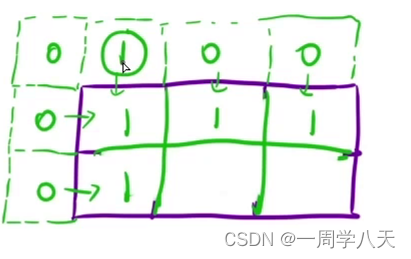

为了确保后面的值是正确的,在1,1的上面或者左边设置一个1即可。
c填表顺序
上到下,左到右
d返回值
dp[m][n]
代码
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int >> dp(m+1,vector<int>(n+1,0));dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};vector初始化

三、不同路径2
1、题目解析
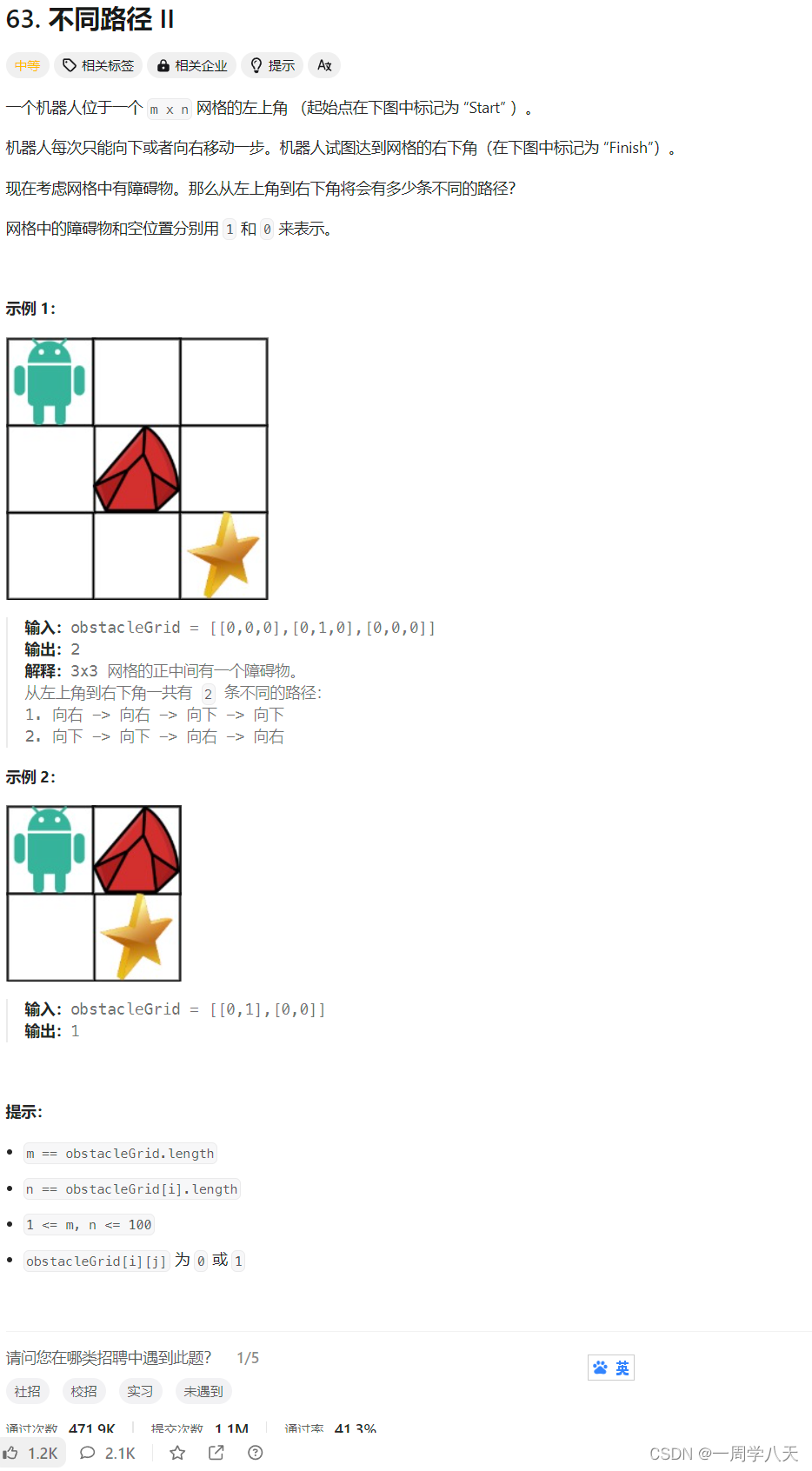
2、算法原理
a.状态表示
dp[i][j]表示起始位置到这里有多少种方法
b.状态转移方程
遇到障碍就不相加,将其视作0,让其保持0 的状态,其他位置相加遇到障碍时就相加也不会有影响。
dp[i][j]=dp[i-1][j]+dp[i][j-1]
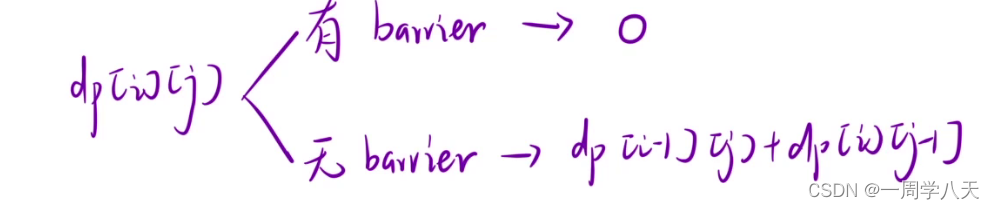
c.初始化
1.用虚拟节点的方法,最重要的是让1,1位置赋值为1就行了,能够保证后续填表的正确。

2.这里的映照关系平特别注意一下
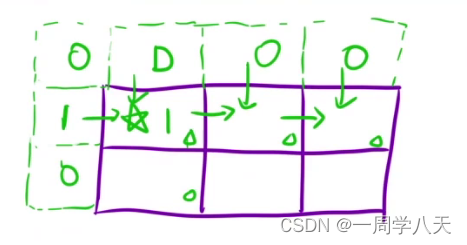
e填表顺序
左到右上到下
e代码
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//创建数组dp//初始化//填表//返回值int m=obstacleGrid.size();int n=obstacleGrid[0].size();vector<vector<int >> dp(m+1,vector<int> (n+1,0));dp[1][0]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(obstacleGrid[i-1][j-1]==0)dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};四、47.礼物最大价值
1、题目解析

就是说从左上往右下走最多能拿多贵的礼物
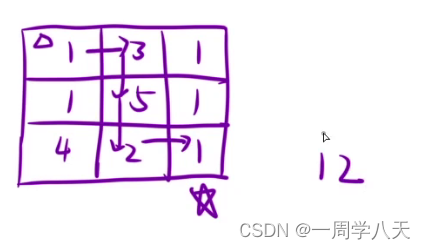
2、算法原理
a状态表示
经验+题目要求
dp[i][j]表示,到这个位置能达到最贵重的礼物
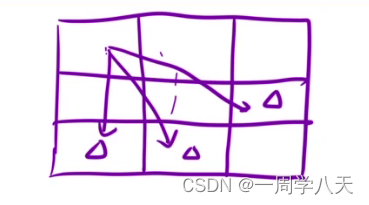
b状态装移方程
根据最近的一步划分问题
观察来时的路,那一条更加贵重一些
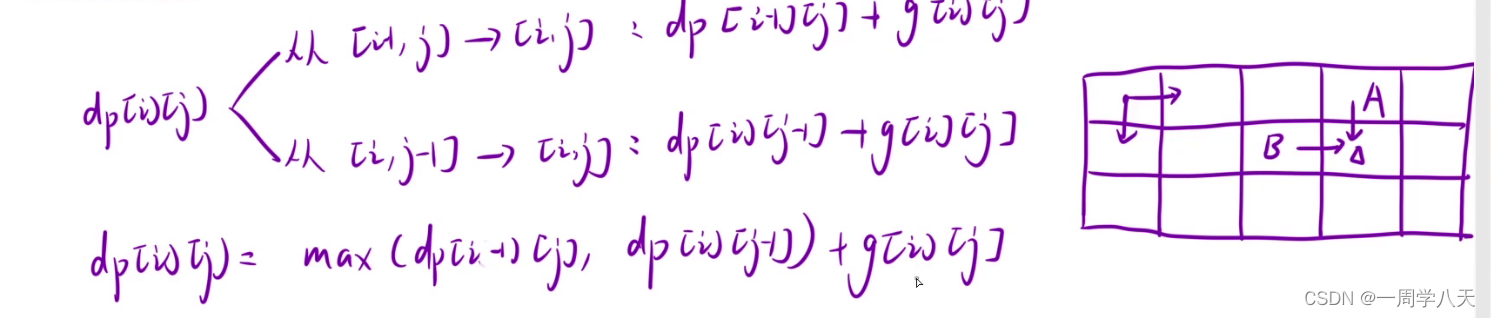
c初始化
1.虚拟节点的值需要保证后续填表时的值是正确的
设置为0即可。
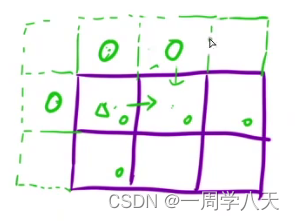
(0,1)和(1,0)位置应该设置为0,不影响1,1位置的取值,(0,2)位置应该设置为负无穷,为了不影响1,1到1,2的取值,但是题目要求说明了输入的价格都是大于零的数,所以我们直接取0即可
2.注意下标映射关系
frame中查找价格时需要将下标-1,
d填表顺序
左上到右下
e返回值
dp[m][n]
f代码
class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {//建dpint m=frame.size(),n=frame[0].size();vector<vector<int>> dp(m+1,vector<int> (n+1,0));//初始化,为0即可//填表for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];}}//返回值return dp[m][n];}
};五、下降路径最小和
1、题目解析
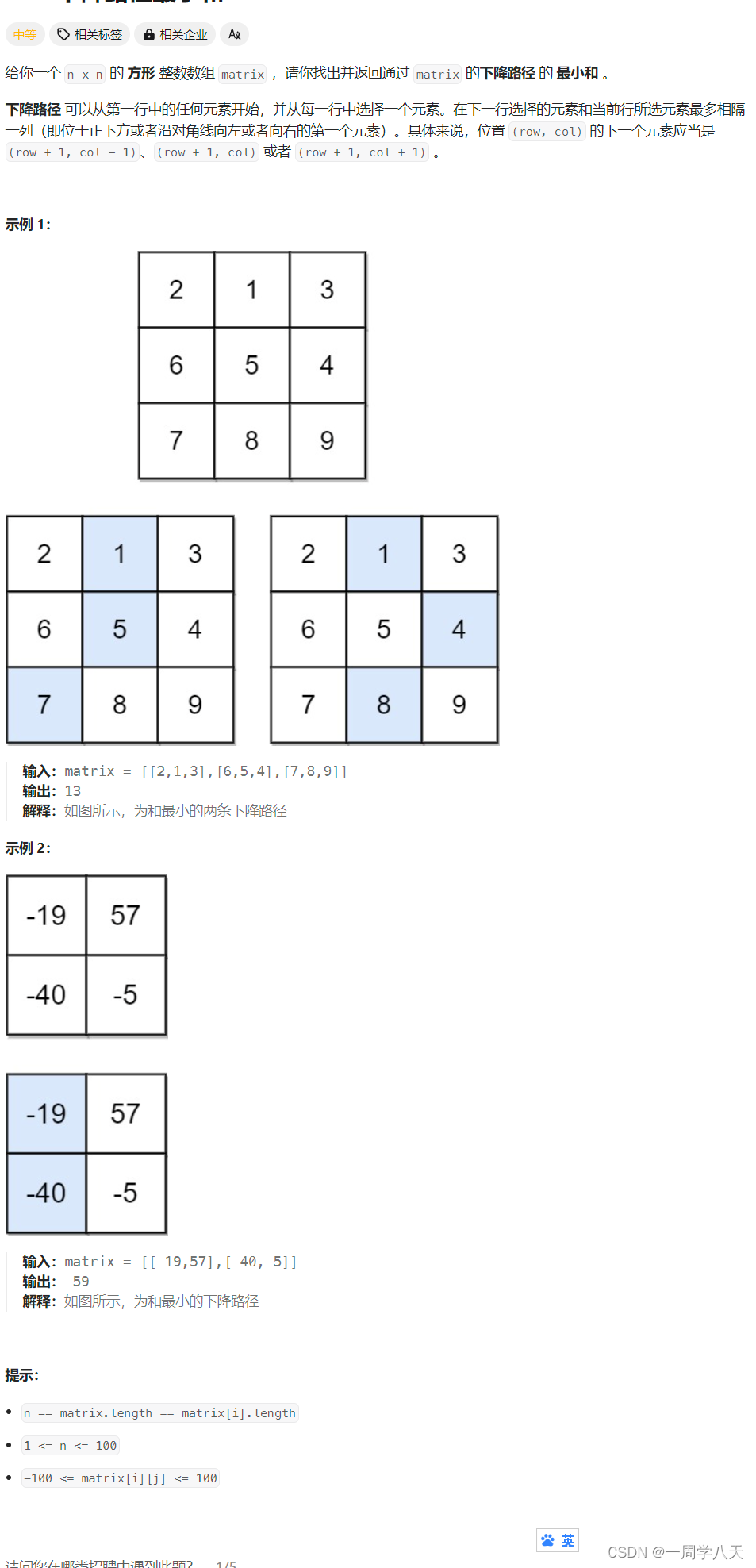
2、算法原理
a状态方程
经验+题目要求
dp[i][j]表示。。。
dp[i][j]表示从上到下最小的路径和
b状态转移方程
不好却低呢是哪一条、路线,但是能保证自己这个节点怎么样最小,细分问题
根据距离dp[i][j]最近的值进行问题划分。
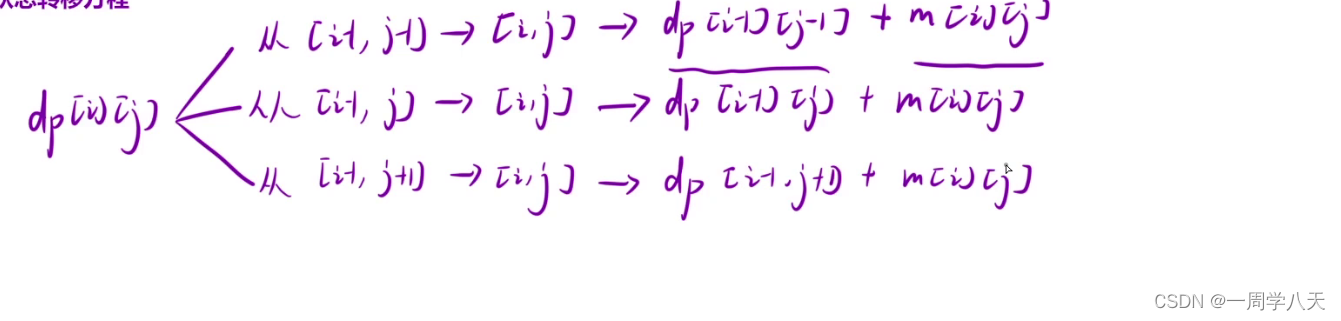
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+m[i][j]
c初始化
1、虚拟节点需要保证后续填表的正确性
第一行设为0,因为要向下相加
第一列最后一列设置为最大值(该值为INT_MAX)
这里非常容易忽视最后一列
2、注意下标映射关系
-1-1
d填表顺序
从左到右,从上到下
e返回值
返回最后一排最小的值
3、代码
class Solution {int my_min(int &a,int &b,int &c){int tem;tem=a<b?a:b;return tem<c?tem:c;}public:int minFallingPathSum(vector<vector<int>>& matrix) {int m=matrix.size();vector<vector<int>> dp(m+1,vector<int>(m+2,INT_MAX));for(int i=0;i<=m;i++){dp[0][i]=0;}//填表for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){dp[i][j]=my_min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i-1][j-1];}}int min=INT_MAX;for(int j=1;j<=m;j++){if(dp[m][j]<min)min=dp[m][j];} return min;}
};