文章目录
- 加锁的基本原则
- 死锁
- 死锁的概念
- 死锁的条件
- 线程同步
- 生产者消费者模型
- 模型的理解
- 理解cp问题
- 条件变量
本篇总结的是关于Linux中锁的相关概念以及生产者消费者模型
加锁的基本原则
加锁的基本原则:谁加锁谁解锁,不要把加锁和解锁这样的操作放在两个线程中
死锁
死锁的概念
下面讲述死锁的一种情况,进而对于死锁有一个较为清楚的认知:
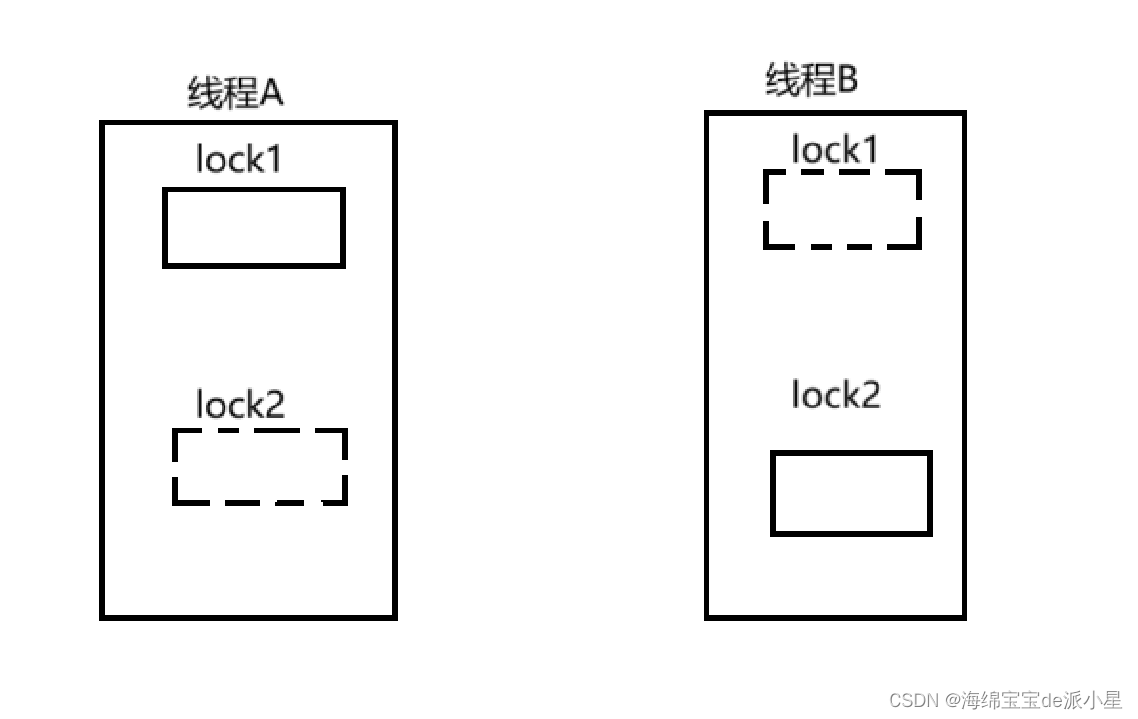
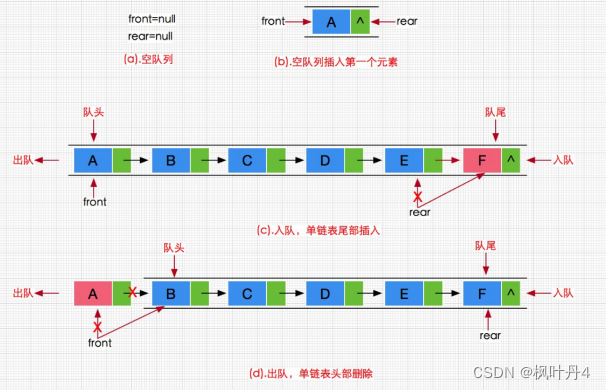
上图展示的是死锁的其中一个场景,对于这个代码块来说,想要访问这部分资源必须需要两个锁,一个是lock1,一个是lock2
那此时有两个线程A和B,对于线程A来说,它现在持有一把锁lock1,对于线程B来说它持有一把锁lock2,但此时这两个线程都无法进入对应的代码块中,此时线程A要访问这块资源,发现条件不足,少一把锁,于是被挂起,线程B要访问这块资源,发现条件不足,少一把锁,于是被挂起,基于这样的原因,这两个线程在之后的每一次被调度都会被阻塞,这就是一个最基本的死锁问题
死锁的条件
互斥条件:一个资源每次只能被一个执行流使用
请求与保持条件:一个执行流因请求资源而阻塞时,对已获得的资源保持不放
不剥夺条件:一个执行流已获得的资源,在末使用完之前,不能强行剥夺
循环等待条件:若干执行流之间形成一种头尾相接的循环等待资源的关系
对比上述的四个条件,再次回到刚才的这个死锁场景
- 互斥条件:代码中间的这部分资源只能被线程A和B当中的一个进行访问,构成了互斥条件
- 请求和保持:线程A和B发生阻塞的时候,不会对于当前它们所持有的锁进行释放,而是占用了现有的这个锁,直到下次被调度
- 不剥夺条件:线程A不能去把线程B当前所持有的锁剥夺下来供自己使用
- 循环等待:线程A和B交替对于锁的申请判断的逻辑构成了一个环的概念
所以,想要构成死锁,必须要满足上述的这四个条件,只要有一个不满足就不应构成死锁,因此也有了另外一个话题,想要破坏死锁,本质上来说只要破坏了这四个条件中的一个就可以了
线程同步
前面讲解了线程互斥的基本原理,那么本节主要讲解关于线程同步的原理,对于线程同步的理解,先给出下面的使用场景:
现有一个线程,拥有一把锁,所以它在以很高的强度对于这个资源进行访问,但是很不幸,处于一些原因,它的访问每次都是无效的,而由于规则的指定失误,这个线程每次都能访问到这个资源,而其他的线程却无法访问到这个资源,这样就造成了线程饥饿的现象出现,那为了解决这样的问题,就给出了线程同步的概念
线程同步是指在多线程编程中,控制多个线程之间的执行顺序和共享资源的访问,以确保数据的一致性和正确性,例如在上面的情景中,可以制定特定的规则,当前线程结束后,必须进行某个队列中进行排队,当排队结束后才能继续进行访问,这样本质上就解决了对于一份共享资源被同一个线程高强度的重复访问,就会造成所谓线程饥饿的现象出现,换句话说,线程同步就是如何合理的使用资源解决线程饥饿的问题,也可以说是让临界资源在使用安全的前提下,让多线程的执行具有一定的顺序性,这个就是所谓线程同步的基本概念
生产者消费者模型
先上定义:
生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯,而通过阻塞队列来进行通讯,所以生产者生产完数据之后不用等待消费者处理,直接扔给阻塞队列,消费者不找生产者要数据,而是直接从阻塞队列里取,阻塞队列就相当于一个缓冲区,平衡了生产者和消费者的处理能力。这个阻塞队列就是用来给生产者和消费者解耦的
模型的理解
对于这个模型的理解,首先从生活的场景入手:在生活中,超市就是一个很经典的生产消费模型,每一个消费者想要获取生产者生产出来的物品,而生产者生产出来的问题要放到超市,超市再把这些内容卖给消费者,就是这样的一个过程
对于这个模型的理解来说,可以把这个生产者看成是线程,而消费者也是线程,那生产者生产的内容交给消费者,这个过程该如何理解?实际上直接把计算机中的数据当成商品就可以
生产者消费者的这个模型,本质上来说就是执行数据流动的过程,把数据由一批线程交由另外一批线程,可以看成是数据流动,也可以是理解为通信的概念,但现在我们抛开这个超市本身的问题,对于供货商来说,想要把自己的商品交到超市里面,所以超市对于供货商来讲本身就是一种临界资源,消费者要到超市中去消费,前提要保证这个过程是安全的,对应到线程的概念来说,就是一批线程要把数据交给另外一批线程,在这个交付的过程中务必要保证是线程安全的
那如何理解线程安全?下面我给出一个线程不安全的例子,比如说现在超市正在供货,但当这个货还没放到货架的时候就被消费者拿走了,那对于超市来说,它其实并不知道这个东西到底是否存放到了货架中,甚至可能在进行统计数量的时候只是统计了放置到货架上的内容,并没有统计这个用户前面拿走的这个内容,这就可以看成是一个数据不安全的问题,对应到线程中也是如此,如果产生了上述这样的类似的问题,那就可以把这个过程看成是不安全的现象
有了上述的概念,下面来理解三个关系
- 生产者和生产者之间的关系:竞争并且互斥,一个货架只能放一种货品,并且总量是保证的,一个供货商的东西放多了,其他供货商自然就没了,并且在一个厂商放东西的时候另外一个不能也放,这叫做互斥
- 消费者和消费者之间的关系:竞争并且互斥,原理和上述相似,货架总共就这么多东西,拿的多的自然就有拿的少的
- 生产者和消费者之间的关系:互斥并且同步,具体理解如下:
互斥性:互斥性确保在同一时间只能有一个线程(生产者或消费者)访问共享资源(缓冲区)。这意味着当一个线程正在对缓冲区进行生产或消费操作时,另一个线程不能同时进行相同的操作。这样可以避免数据竞争和数据不一致的问题。
同步性:同步性确保生产者和消费者之间的操作是协调一致的,即当生产者生产了数据并放入缓冲区后,消费者必须能够及时地从缓冲区中取出数据进行处理;反之,当缓冲区为空时,消费者必须等待生产者生产数据。同样地,当缓冲区已满时,生产者必须等待消费者消费数据
理解cp问题
CP 问题通常是指"Consumer-Producer"(消费者-生产者)问题,那下面先举一个这样的例子
假设现在有函数调用,在main函数中函数执行的很快,但是如果跳转到函数体内部,就执行的很慢,那么此时外部的这个main函数就必须要等待内部的函数调用执行结束后才能进行继续的调用,那这个过程就是普通的单线程可能会经常遇到的一个情景
那能不能设计这样的一个情景,使得这个执行快的这部分一直很快,慢的部分一直很慢,两个执行流互不干扰呢?那cp问题就可以解决这样的情景,cp问题的主要目的就是实现一个多执行流之间的执行解耦问题,线程在不断的把数据很快的输送到一个地方,而另外一批线程正在慢慢的进行数据的计算等,这个逻辑和前面的超市的逻辑一样,如果按照单线程的理解来说,供货商的生产速度很快,但是消费者消费的很慢,供货商必须等消费者消费结束后才能继续供货,这样必然会导致效率的问题,因此就有了生产消费模型,供货商快速的生产,把货放到超市里面,而消费者只需要慢慢的对这些货进行消费就可以了,把供货商和消费者之间的关系进行了一个解耦,这样就实现了想要形成的一个状态
换句话说这是一个忙闲不均的问题,生产的这一端很忙,在不停的向这段空间中扔数据,而消费的却闲,但不影响生产继续生产,这就是因为有这段空间带来的好处
条件变量
在生产消费模型中,条件变量是一个很重要的概念,再以超市为例,当货物还没有就绪的时候,消费者如果要在超市中申请货物是申请不到的,而频繁的进行申请可能还会带来影响供货的速度,那为了解决这样的问题就引入了条件变量的概念,可以把条件变量理解为一个提醒器,在货物就绪的时候就提醒消费者,可以进行消费了,这样就避免了消费者在进行频繁申请却没有成果带来的这样的弊端