---------------🎈🎈669. 修剪二叉搜索树 题目链接🎈🎈-------------------

解法1 递归 反复做吧

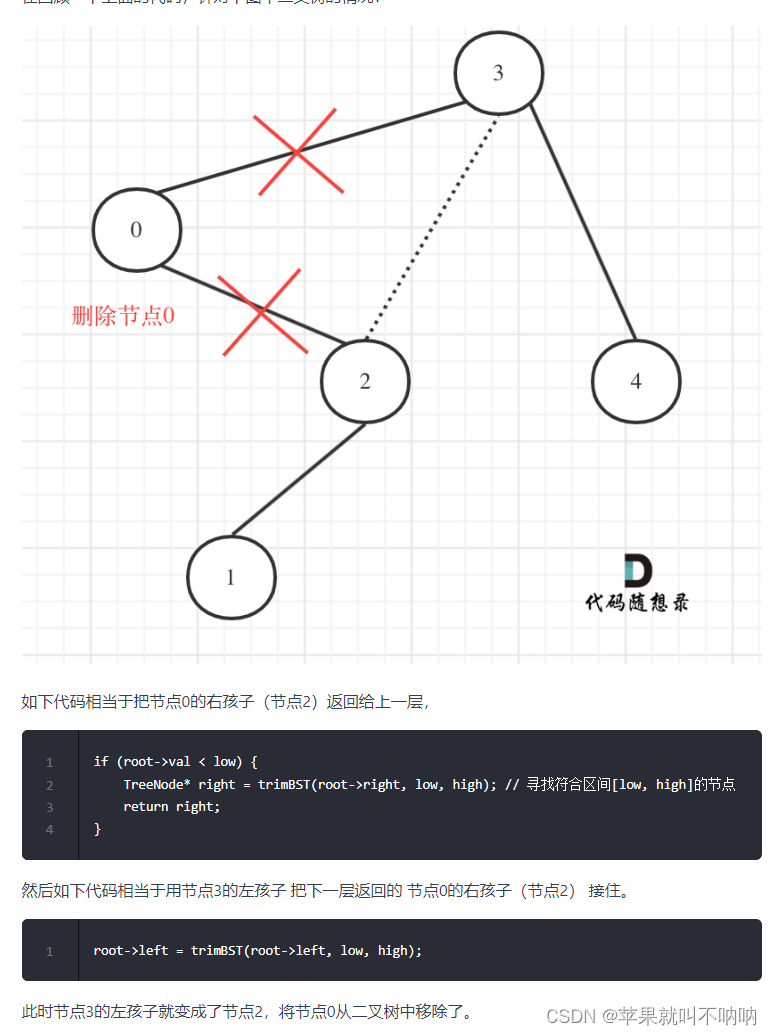
/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/class Solution {  // 删除小于low 大于high的节点public TreeNode trimBST(TreeNode root, int low, int high) {if(root == null){return null;}// 如果当前节点小于low 那么就去继续递归当前节点的右子树（右子树可能大于low） 结果即为修剪后的当前节点的右子树 返回right（返回的就是右子树头结点）if(root.val < low){TreeNode right = trimBST(root.right, low, high);return right;}// 如果当前节点大于high 那么就去继续递归当前节点的左子树（左子树可能小于high） 结果即为修剪后的当前节点的左子树 返回left（返回的就是左子树头结点）if(root.val > high){TreeNode left =  trimBST(root.left, low, high);return left;}root.left = trimBST(root.left,low,high);root.right = trimBST(root.right,low,high);return root;}
}