1. 发起请求

客户端通过 HTTP 协议向服务器发起请求。

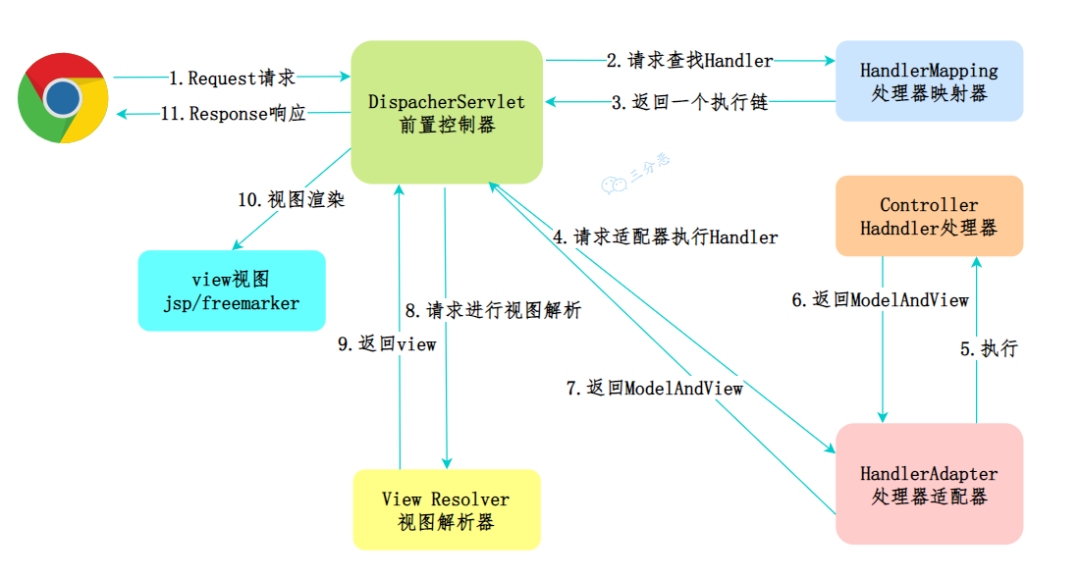
2. 前端控制器（DispatcherServlet）

这个请求会先到前端控制器 DispatcherServlet，它是整个流程的入口点，负责接收请求并将其分发给相应的处理器。

3. 处理器映射（HandlerMapping）

DispatcherServlet 调用 HandlerMapping 来确定哪个 Controller 应该处理这个请求。通常会根据请求的 URL 来确定

4. 处理器适配器（HandlerAdapter）

一旦找到目标 Controller，DispatcherServlet 会使用 HandlerAdapter 来调用 Controller 的处理方法

5. 执行处理器（Controller）

Controller 处理请求，处理完后返回一个 ModelAndView 对象，其中包含模型数据和逻辑视图名

6. 视图解析器（ViewResolver）

DispatcherServlet 接收到 ModelAndView 后，会使用 ViewResolver 来解析视图名称，找到具体的视图页面

7. 渲染视图

视图使用模型数据渲染页面，生成最终的页面内容

8. 响应结果

DispatcherServlet 将视图结果返回给客户端

---

在前后端分离的情况下，步骤 ⑥、⑦、⑧ 会略有不同，后端通常只需要处理数据，并将 JSON 格式的数据返回给前端就可以了，而不是返回完整的视图页面。

---

👨‍🏫 参考地址