优质博文IT-BLOG-CN
一、题目
给定两个大小分别为m和n的正序(从小到大)数组nums1和nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组= [1,2,3],中位数2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组= [1,2,3,4],中位数(2 + 3) / 2 = 2.5
nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
二、代码
二分查找
给定两个有序数组,要求找到两个有序数组的中位数,最直观的思路有以下两种:
【1】使用归并的方式,合并两个有序数组,得到一个大的有序数组。大的有序数组的中间位置的元素,即为中位数。
【2】不需要合并两个有序数组,只要找到中位数的位置即可。由于两个数组的长度已知,因此中位数对应的两个数组的下标之和也是已知的。维护两个指针,初始时分别指向两个数组的下标0的位置,每次将指向较小值的指针后移一位(如果一个指针已经到达数组末尾,则只需要移动另一个数组的指针),直到到达中位数的位置。
假设两个有序数组的长度分别为m和n,上述两种思路的复杂度如何?
第一种思路的时间复杂度是O(m+n),空间复杂度是O(m+n)。第二种思路虽然可以将空间复杂度降到O(1),但是时间复杂度仍是 O(m+n)。
如何把时间复杂度降低到O(log(m+n))呢?如果对时间复杂度的要求有log,通常都需要用到二分查找,这道题也可以通过二分查找实现。
根据中位数的定义,当m+n是奇数时,中位数是两个有序数组中的第 (m+n)/2个元素,当m+n是偶数时,中位数是两个有序数组中的第(m+n)/2个元素和第(m+n)/2+1个元素的平均值。因此,这道题可以转化成寻找两个有序数组中的第k小的数,其中k为(m+n)/2或(m+n)/2+1。
假设两个有序数组分别是A和B。要找到第k个元素,我们可以比较A[k/2−1]和B[k/2−1],其中/表示整数除法。由于A[k/2−1]和B[k/2−1]的前面分别有A[0 .. k/2−2]和B[0 .. k/2−2],即k/2−1个元素,对于A[k/2−1]和B[k/2−1]中的较小值,最多只会有 (k/2−1)+(k/2−1)≤k−2(k/2-1)+(k/2-1)个元素比它小,那么它就不能是第k小的数了。
因此我们可以归纳出三种情况:
【1】如果A[k/2−1]<B[k/2−1],则比A[k/2−1]小的数最多只有A的前k/2−1个数和B的前k/2−1个数,即比A[k/2−1]小的数最多只有k−2个,因此A[k/2−1]不可能是第k个数,A[0]到A[k/2−1]也都不可能是第k个数,可以全部排除。
【2】如果A[k/2−1]>B[k/2−1],则可以排除B[0]到B[k/2−1]。
【3】如果A[k/2−1]=B[k/2−1],则可以归入第一种情况处理。
比较A[k/2−1]和B[k/2−1]之后,可以排除k/2个不可能是第k小的数,查找范围缩小了一半。同时,我们将在排除后的新数组上继续进行二分查找,并且根据我们排除数的个数,减少k的值,这是因为我们排除的数都不大于第k小的数。
有以下三种情况需要特殊处理:
【1】如果A[k/2−1]或者B[k/2−1]越界,那么我们可以选取对应数组中的最后一个元素。在这种情况下,我们必须根据排除数的个数减少k的值,而不能直接将k减去k/2。
【2】如果一个数组为空,说明该数组中的所有元素都被排除,我们可以直接返回另一个数组中第k小的元素。
【3】如果k=1,我们只要返回两个数组首元素的最小值即可。
用一个例子说明上述算法。假设两个有序数组如下:
A: 1 3 4 9
B: 1 2 3 4 5 6 7 8 9
两个有序数组的长度分别是4和9,长度之和是13,中位数是两个有序数组中的第7个元素,因此需要找到第k=7个元素。
比较两个有序数组中下标为k/2−1=2的数,即A[2]和B[2],如下面所示:
A: 1 3 4 9↑
B: 1 2 3 4 5 6 7 8 9↑
由于A[2]>B[2],因此排除B[0]到B[2],即数组B的下标偏移offset变为3,同时更新 k的值:k=k−k/2=4。
下一步寻找,比较两个有序数组中下标为k/2−1=1的数,即A[1]和B[4],如下面所示,其中方括号部分表示已经被排除的数。
A: 1 3 4 9↑
B: [1 2 3] 4 5 6 7 8 9↑
由于A[1]<B[4],因此排除A[0]到A[1],即数组A的下标偏移变为2,同时更新k的值:k=k−k/2=2。
下一步寻找,比较两个有序数组中下标为k/2−1=0的数,即比较A[2]和B[3],如下面所示,其中方括号部分表示已经被排除的数。
A: [1 3] 4 9↑
B: [1 2 3] 4 5 6 7 8 9↑
由于A[2]=B[3],根据之前的规则,排除A中的元素,因此排除A[2],即数组A的下标偏移变为 3,同时更新k的值: k=k−k/2=1。
由于k的值变成1,因此比较两个有序数组中的未排除下标范围内的第一个数,其中较小的数即为第k个数,由于 A[3]>B[3],因此第k个数是B[3]=4。
A: [1 3 4] 9↑
B: [1 2 3] 4 5 6 7 8 9↑
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int length1 = nums1.length, length2 = nums2.length;int totalLength = length1 + length2;if (totalLength % 2 == 1) {int midIndex = totalLength / 2;double median = getKthElement(nums1, nums2, midIndex + 1);return median;} else {int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;return median;}}public int getKthElement(int[] nums1, int[] nums2, int k) {/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较* 这里的 "/" 表示整除* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个* 这样 pivot 本身最大也只能是第 k-1 小的元素* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数*/int length1 = nums1.length, length2 = nums2.length;int index1 = 0, index2 = 0;int kthElement = 0;while (true) {// 边界情况if (index1 == length1) {return nums2[index2 + k - 1];}if (index2 == length2) {return nums1[index1 + k - 1];}if (k == 1) {return Math.min(nums1[index1], nums2[index2]);}// 正常情况int half = k / 2;int newIndex1 = Math.min(index1 + half, length1) - 1;int newIndex2 = Math.min(index2 + half, length2) - 1;int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];if (pivot1 <= pivot2) {k -= (newIndex1 - index1 + 1);index1 = newIndex1 + 1;} else {k -= (newIndex2 - index2 + 1);index2 = newIndex2 + 1;}}}
}
时间复杂度: O(log(m+n)),其中m和n分别是数组nums1和nums2的长度。初始时有k=(m+n)/2或k=(m+n)/2+1,每一轮循环可以将查找范围减少一半,因此时间复杂度是O(log(m+n))。
空间复杂度: O(1)。
划分数组
方法一的时间复杂度已经很优秀了,但本题存在时间复杂度更低的一种方法。这里给出推导过程,勇于挑战自己的读者可以进行尝试。
为了使用划分的方法解决这个问题,需要理解「中位数的作用是什么」。在统计中,中位数被用来:将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
如果理解了中位数的划分作用,就很接近答案了。
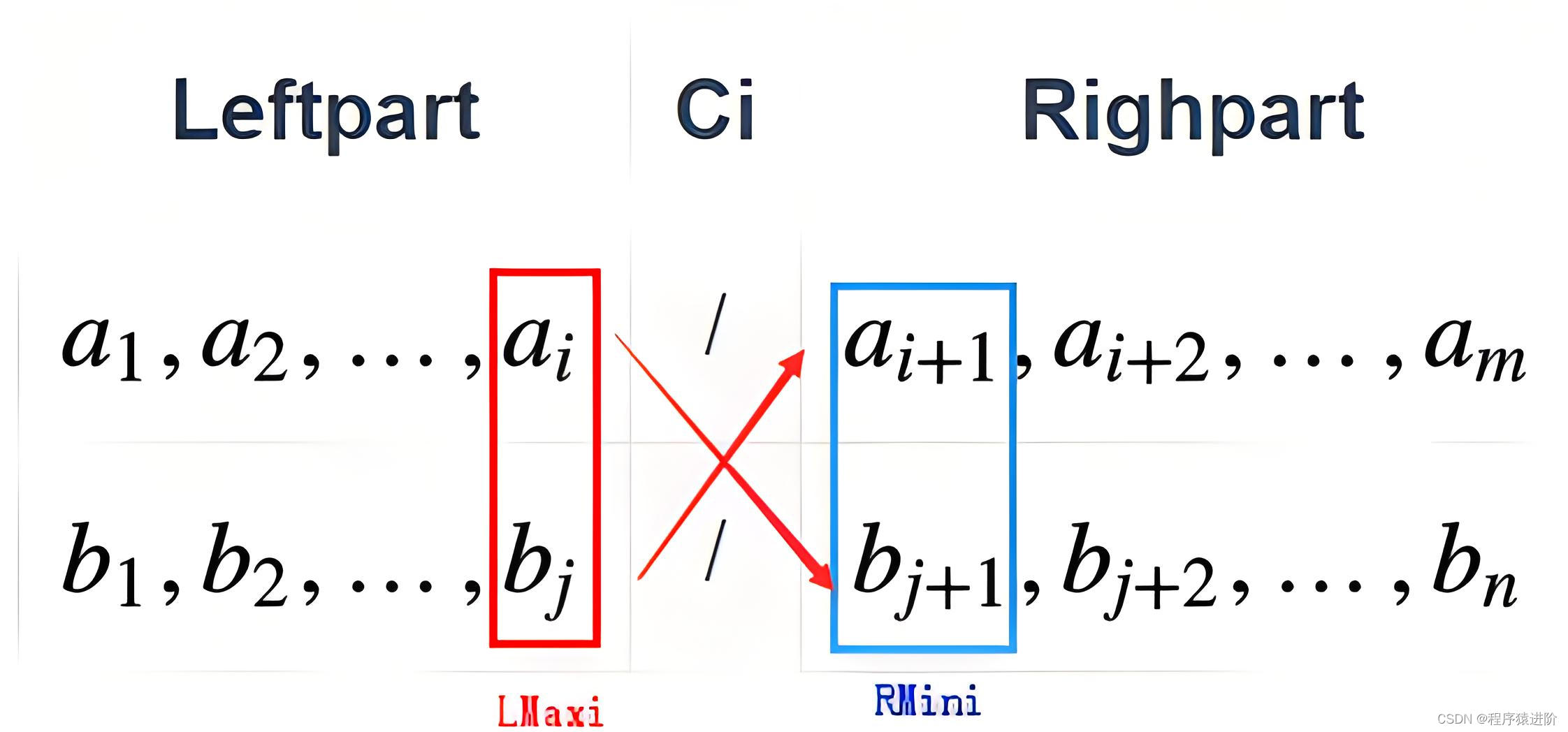
首先,在任意位置i将A划分成两个部分:
left_A | right_AA[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
由于A中有m个元素, 所以有m+1种划分的方法(i∈[0,m]i \in [0, m]i∈[0,m])。
len(left_A)=i,len(right_A)=m−i
注意: 当i=0时,left_A为空集, 而当i=m时, right_A为空集。
采用同样的方式,在任意位置j将B划分成两个部分:
left_B | right_BB[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
将left_A和left_B放入一个集合,并将right_A和right_B放入另一个集合。 再把这两个新的集合分别命名为left_part和right_part:
left_part | right_partA[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
当A和B的总长度是偶数时,如果可以确认:
len(left_part)=len(right_part)
max(left_part)≤min(right_part)
那么,{A,B}中的所有元素已经被划分为相同长度的两个部分,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值和后一部分的最小值的平均值:median=max(left_part)+min(right_part)2
当A和B的总长度是奇数时,如果可以确认:
len(left_part)=len(right_part)+1
max(left_part)≤min(right_part)
那么,{A,B}中的所有元素已经被划分为两个部分,前一部分比后一部分多一个元素,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值:median=max(left_part)
第一个条件对于总长度是偶数和奇数的情况有所不同,但是可以将两种情况合并。第二个条件对于总长度是偶数和奇数的情况是一样的。
要确保这两个条件,只需要保证:i+j=m−i+n−j(当m+n为偶数)或i+j=m−i+n−j+1(当m+n为奇数)。等号左侧为前一部分的元素个数,等号右侧为后一部分的元素个数。将i和j全部移到等号左侧,我们就可以得到i+j=(m+n+1)/2。这里的分数结果只保留整数部分。
0≤i≤m,0≤j≤n。如果我们规定A的长度小于等于B的长度,即m≤。这样对于任意的i∈[0,m],都有j=m+n+12−i∈[0,n],那么我们在[0,m]的范围内枚举i并得到j,就不需要额外的性质了。
【1】如果A的长度较大,那么我们只要交换A和B即可。
【2】如果m>n,那么得出的j有可能是负数。
B[j−1]≤A[i]以及A[i−1]≤B[j],即前一部分的最大值小于等于后一部分的最小值。
为了简化分析,假设A[i−1],B[j−1],A[i],B[j]总是存在。对于i=0、i=m、j=0、j=n这样的临界条件,我们只需要规定A[−1]=B[−1]=−∞,A[m]=B[n]=∞即可。这也是比较直观的:当一个数组不出现在前一部分时,对应的值为负无穷,就不会对前一部分的最大值产生影响;当一个数组不出现在后一部分时,对应的值为正无穷,就不会对后一部分的最小值产生影响。
所以我们需要做的是: 在[0,m]中找到i,使得:B[j−1]≤A[i]且A[i−1]≤B[j],其中j=m+n+12−i
我们证明它等价于: 在[0,m]中找到最大的i,使得:A[i−1]≤B[j],其中j=m+n+12−i
这是因为:
【1】当i从0∼m递增时,A[i−1]递增,B[j]递减,所以一定存在一个最大的i满足A[i−1]≤B[j];
【2】如果i是最大的,那么说明i+1不满足。将i+1带入可以得到A[i]>B[j−1],也就是B[j−1]<A[i],就和我们进行等价变换前i的性质一致了(甚至还要更强)。
因此我们可以对i在[0,m]的区间上进行二分搜索,找到最大的满足A[i−1]≤B[j]的i值,就得到了划分的方法。此时,划分前一部分元素中的最大值,以及划分后一部分元素中的最小值,才可能作为就是这两个数组的中位数。
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {if (nums1.length > nums2.length) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.length;int n = nums2.length;int left = 0, right = m;// median1:前一部分的最大值// median2:后一部分的最小值int median1 = 0, median2 = 0;while (left <= right) {// 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]// 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]int i = (left + right) / 2;int j = (m + n + 1) / 2 - i;// nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);if (nums_im1 <= nums_j) {median1 = Math.max(nums_im1, nums_jm1);median2 = Math.min(nums_i, nums_j);left = i + 1;} else {right = i - 1;}}return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;}
}
时间复杂度: O(logmin(m,n))),其中m和n分别是数组nums1和nums2的长度。查找的区间是[0,m],而该区间的长度在每次循环之后都会减少为原来的一半。所以,只需要执行logm次循环。由于每次循环中的操作次数是常数,所以时间复杂度为O(logm)。由于我们可能需要交换nums1和nums2使得m≤n,因此时间复杂度是O(logmin(m,n)))。
空间复杂度: O(1)。