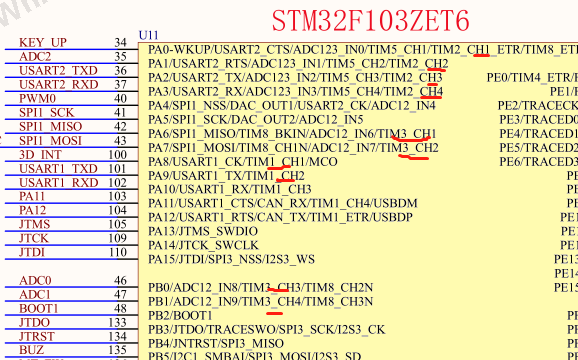
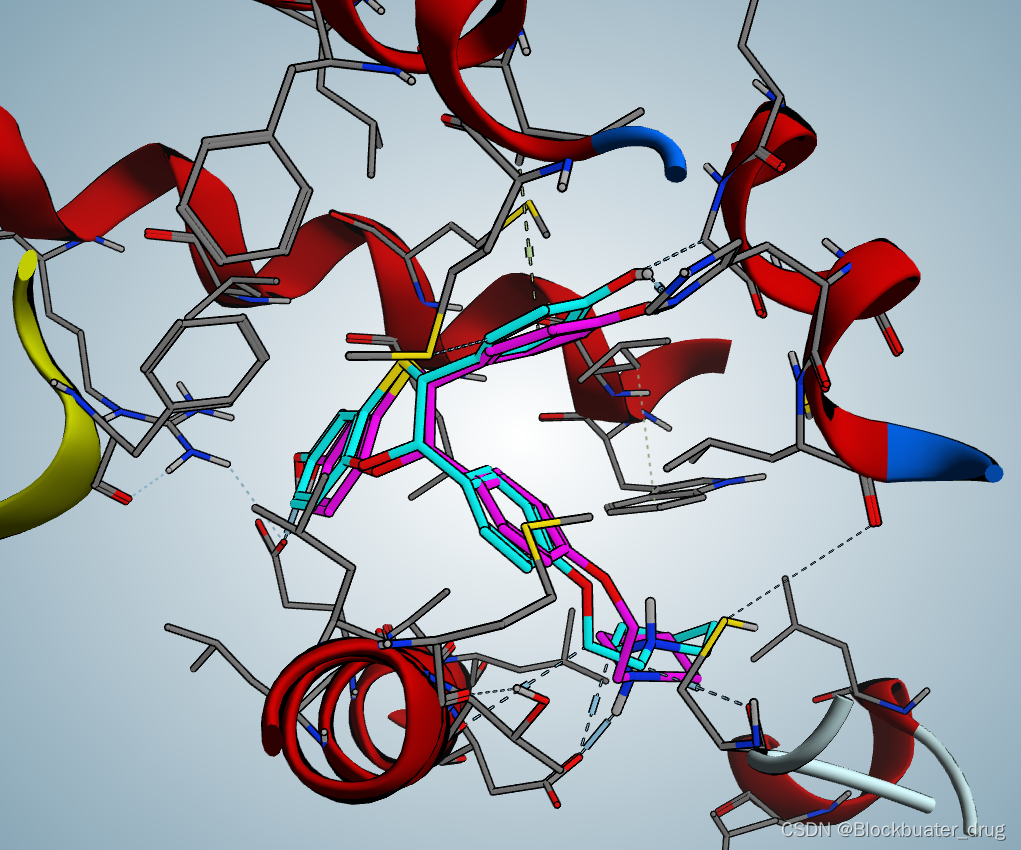
多元正态分布（Multivariate Normal Distribution），也称为多变量高斯分布，是单变量正态分布（高斯分布）在多维空间中的推广。它是描述位于多维空间中的随机向量的分布情况的一种概率分布。多元正态分布在统计分析、机器学习、模式识别等多个领域有着广泛的应用。
在数学上，一个n维随机向量 $\mathbf{X}=[X_1,X_2,\dots ,X_n{]}^T$ 如果服从多元正态分布，可以用以下的密度函数来描述：
$f(\mathbf{x};\mathbf{\mu },\mathbf{\Sigma })=\frac{1}{\sqrt{(2\pi {)}^n|\mathbf{\Sigma }|}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right)$
其中：

• $\mathbf{x}$ 是一个具体的实数向量 $[x_1,x_2,\dots ,x_n{]}^T$。
• $\mathbf{\mu }$ 是一个n维均值向量 $[{\mu }_1,{\mu }_2,\dots ,{\mu }_n{]}^T$，表示各个分量的平均值。
• $\mathbf{\Sigma }$是一个$n\times n$的协方差矩阵，表示各分量之间的协方差，描述了变量之间的相关性。矩阵 $\mathbf{\Sigma }$必须是对称的和半正定的。
• $|\mathbf{\Sigma }|$ 是协方差矩阵的行列式。

特征：

1. 每个分量 $X_i$ 自身是正态分布的。
2. 任意两个分量 $X_i$ 和 $X_j$ 的线性组合也服从正态分布。
3. 分量之间可以是相互独立的，如果协方差矩阵 $\mathbf{\Sigma }$是对角矩阵；如果协方差矩阵是单位矩阵，且各随机变量有相同的方差，则这些变量不仅相互独立，而且是标准正态分布的。
4. 多元正态分布的概率密度函数的等高线总是椭球型的，其形状、大小和方向取决于均值向量 $\mathbf{\mu }$ 和协方差矩阵$\mathbf{\Sigma }$。
5. 协方差矩阵的特征值和特征向量决定了这些椭球的方向和轴的长度。

在实际应用中，参数 $\mathbf{\mu }$和 $\mathbf{\Sigma }$ 通常通过样本的均值和样本协方差矩阵来估计。多元正态分布是许多多变量统计方法的基础，如多变量回归分析、主成分分析（PCA）等。

多元正态分布的性质主要包括以下几点：

1. 线性变换：

• 如果一个随机向量 $\mathbf{X}$ 服从多元正态分布 $N(\mathbf{\mu },\mathbf{\Sigma })$，则对于任意线性变换 $\mathbf{AX}+\mathbf{b}$，其中$\mathbf{A}$ 是一个常数矩阵，$\mathbf{b}$ 是一个常数向量，变换后的随机向量也服从多元正态分布。

2. 边缘分布：

• 多元正态随机向量的任何子集也服从多元正态分布。例如，如果 $\mathbf{X}$ 是一个多元正态分布，那么$\mathbf{X}$中的任何元素或者元素的子集也是正态分布的。

3. 条件分布：

• 在多元正态分布中，条件分布也是正态分布。也就是说，一个或多个变量给定条件下其他变量的分布仍然是正态分布。

4. 独立性：

• 如果两个或多个随机变量之间的协方差为零，则这些随机变量在多元正态分布中是独立的。

5. 非奇异协方差矩阵：

• 多元正态分布要求协方差矩阵 $\mathbf{\Sigma }$是非奇异的，即 $\mathbf{\Sigma }$的行列式不为零。这意味着所有变量都有正方差，且没有完全的线性关系。

6. 概率密度函数的形状：

• 当协方差矩阵是对角矩阵时，各个变量之间独立，概率密度函数的等高线是轴对齐的椭圆形（或超椭球形）。当协方差矩阵具有非对角线元素时，等高线会旋转和倾斜，反映出变量之间的相关性。

7. 均值向量和协方差矩阵的决定作用：

• 均值向量$\mathbf{\mu }$确定了多元正态分布的中心位置，而协方差矩阵$\mathbf{\Sigma }$ 决定了分布的形状和变量间的相关性。

8. 无偏估计：

• 样本均值和样本协方差矩阵是多元正态分布参数的无偏估计。

9. 最大熵性质：

• 在给定均值向量和协方差矩阵的条件下，多元正态分布具有最大熵，这意味着它在所有可能的概率分布中具有最大的不确定性。这使得多元正态分布在自然界和社会科学中的数据建模中非常普遍。

这些性质使得多元正态分布在理论研究和实际应用中都非常重要，尤其是在统计推断、风险管理、机器学习和许多其他领域。

在多元正态分布中，有些特殊的情况是值得注意的：

1. 标准多元正态分布:

• 当均值向量 $\mathbf{\mu }$是零向量，协方差矩阵$\mathbf{\Sigma }$是单位矩阵时，即所有随机变量都有均值 0 和方差 1，且彼此独立，这种多元正态分布称为标准多元正态分布。

2. 各向同性多元正态分布:

• 如果协方差矩阵$\mathbf{\Sigma }$是一个标量乘以单位矩阵，即${\sigma }^2\mathbf{I}$，这表明所有变量都有相同的方差${\sigma }^2$，并且彼此独立。这种分布的等高线在空间中具有各向同性的性质，无论从哪个方向看都是相同的。

3. 相关多元正态分布:

• 当协方差矩阵的非对角线元素不为零时，不同变量之间存在线性相关性。相关性由协方差矩阵的非对角元素的符号和大小确定。

4. 退化多元正态分布:

• 如果协方差矩阵$\mathbf{\Sigma }$ 的行列式为零，也就是说矩阵不是满秩的，那么这个多元正态分布被称为退化的。在这种情况下，随机变量间存在完全的线性关系，导致分布不再有一个良好定义的密度。退化分布的支持是在一个维度低于其变量数的空间中。

5. 条件多元正态分布:

• 在多元正态分布中，给定一些变量值后，剩余变量的条件分布仍然是多元正态分布。条件分布的均值和协方差可以通过已知变量的值计算得出。

6. 截断多元正态分布:

• 当多元正态分布在某些区域被截断时，例如某些变量只能取正值，那么在这个区域内的分布是截断多元正态分布。

上述特殊情况下的多元正态分布在理论探讨和实际应用中都有重要的地位，比如在金融模型、社会科学研究、工程问题等领域。