定义:逻辑回归是一种用于解决分类问题的统计学习方法。它通过对数据进行建模,预测一个事件发生的概率。逻辑回归通常用于二元分类问题,即将数据分为两个类别。它基于线性回归模型,但使用了逻辑函数(也称为S形函数)来将输出限制在0到1之间,表示事件发生的概率。逻辑回归可以通过最大似然估计或梯度下降等方法来进行参数估计,从而得到一个可以用于分类的模型。
一、逻辑回归入门
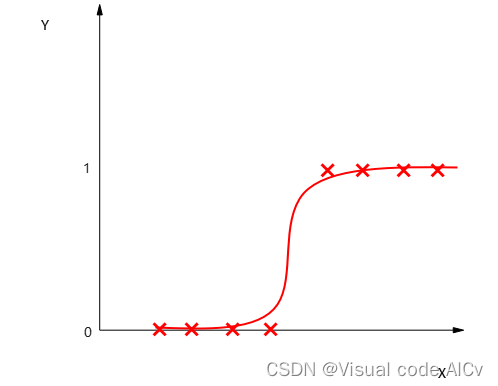
在分类肿瘤的例子中,我们将肿瘤分为恶性肿瘤和良性肿瘤。 对于恶性肿瘤赋值1(yes),对良性肿瘤赋值0(no)。并在坐标系中表示出其数据集以及对应的拟合曲线如下:

二、逻辑函数(对数几率函数)
沿用上面的例子,假设原始数据集有一个值为0.7,我们应该如何来在坐标系中表示呢? 我们需要引用一个逻辑函数来描述这些位于0~1中间的数据。
在所有的二分类问题中,我们需要将实值Z准华为0/1的值,最理想的函数肯定是分段函数(单位阶跃函数):
但是分段函数不连续,因此不能单调可微调函数转化为线性模型。所以我们希望找到一个用于替代分段函数的“近似替代函数”,希望它能够单调可微。逻辑函数(Sigmoid function)正是这样一个函数:
(1)
当我们将逻辑函数作为带入(1)式中可得:
(2)
经过变换后得到:
(3)
若将y视作样本x为正例(恶性肿瘤)的可能性,则1-y是其反比的可能性,两者的比值称为几率(odds),反映了x作为正例的相对可能性。按照通俗的话来说,我们可以视逻辑回归的输出结果为对于给定的输入x情况下输出y=1的概率。
还是以肿瘤的例子说明:其中x为肿瘤尺寸,y为良性肿瘤0和恶性肿瘤1,如果从上述(2)中得到y=0.7,则说明对于x有70%的概率为恶性肿瘤。 
逻辑函数常见形式:
三、决策边界
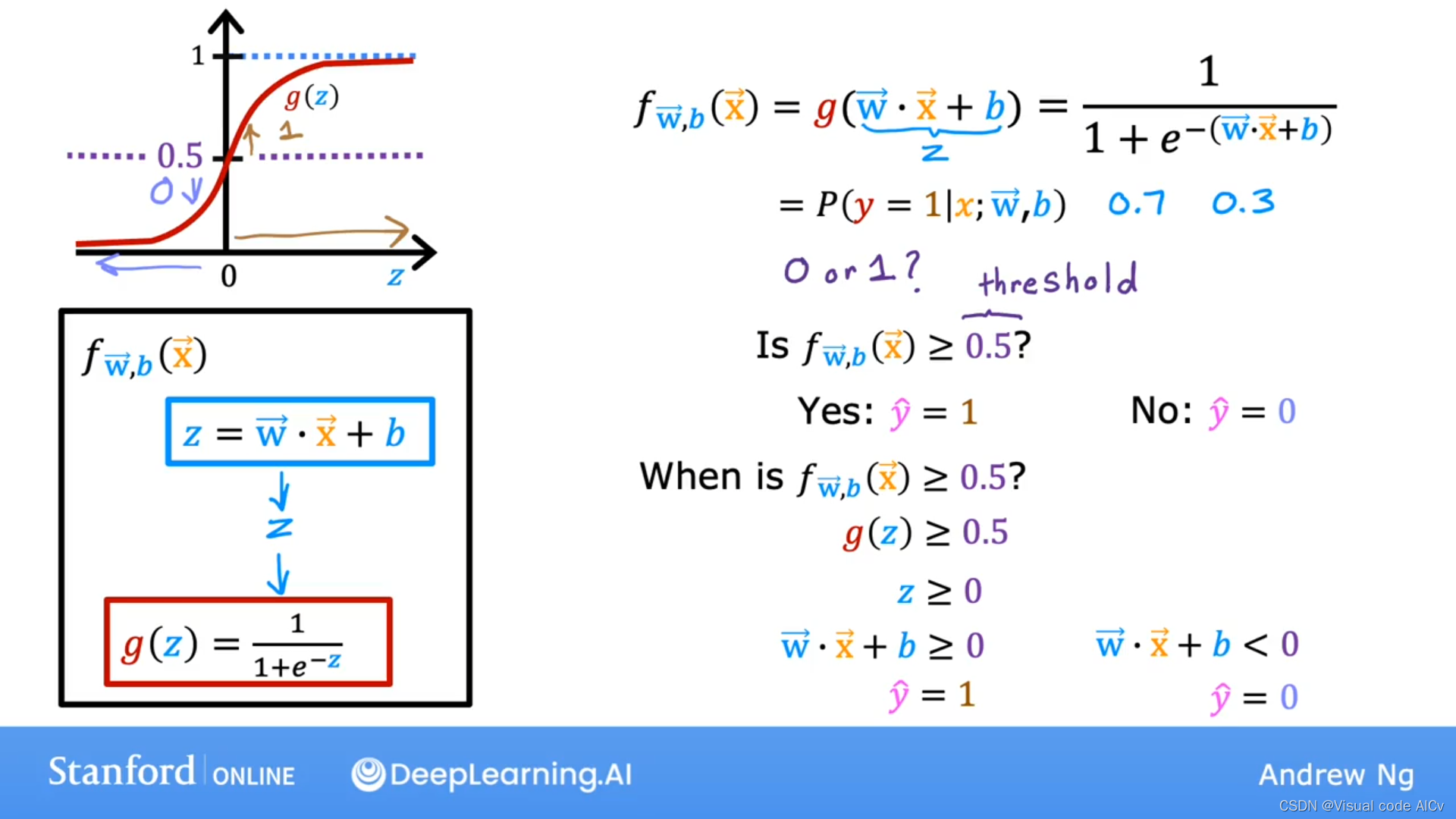
在分类问题中,通过逻辑回归得到的输出只会是确定的整数;我们必须找到一个介于0~1之间的阈值flag作为决策边界。
判断的基本形式如下:通过样本值与flag进行比较来分类;
Is
Yes:
No:
因此,我们需要确定何时的点;
有逻辑函数的基本变形形式可知在此时必有:
因此我们可以将作为决策边界
非线性的决策边界
分析决策边界的函数我们不难发现,对于非线性的决策边界我们可以综合多项式回归的知识进行求解。如下图中,使用作为决策边界。

对于多元线性回归也可以同样推导

![[自动驾驶算法][从0开始轨迹预测]:二、自动驾驶系统中常用的坐标系及相应的转换关系](https://img-blog.csdnimg.cn/direct/8f775186530c4a2891335c73f900dada.png#pic_center)