统计学-R语言-4.3

news/2024/7/27 16:52:28/文章来源:https://blog.csdn.net/2301_77225918/article/details/135569044

文章目录

前言
直方图
茎叶图
箱线图
练习

前言

本篇介绍的是数值型数据怎么进行数据可视化，本篇介绍的有直方图、茎叶图、箱线图。

直方图

直方图（Histogram）用于描述连续型变量的频数分布，实际应用中常用于考察变量的分布是否对称；是否服从某种分布类型，如正态分布
直方图以矩形的面积表示各组段的频数或频率，各矩形的面积总和为总频数（或等于1，此时是按照频率来计算的）
在R软件里用函数是hist()来作直方图，把probability参数设置为T是用频率作直方图，默认为F。
示例如下：
代码：

salary=c(2000,2100,2200,2350,2500,2900,3500,3800,2600,3300,3200,4000,4100,3100,4200)
par(mfrow=c(1,2))
hist(salary,main="工资的直方图")
hist(salary,main="工资的直图",probability=T)

继续对工资数据作直方图，结果如下图。
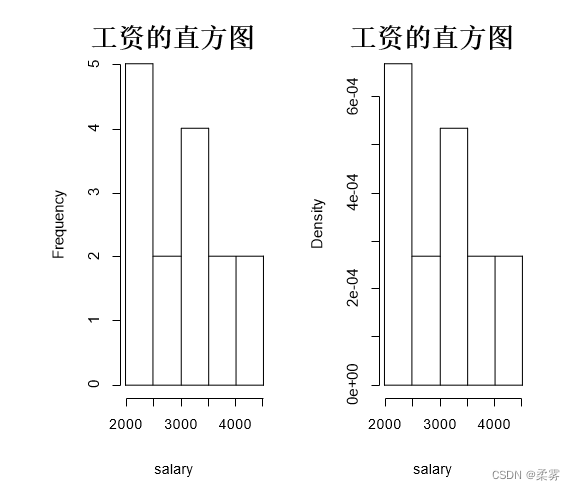
在这里插入图片描述
在R里还可以使用rug()函数把各个数据竖线(轴须线)描绘在X轴上，结果如下所示：

hist(salary,main="工资的直图",probability=T);rug(salary)

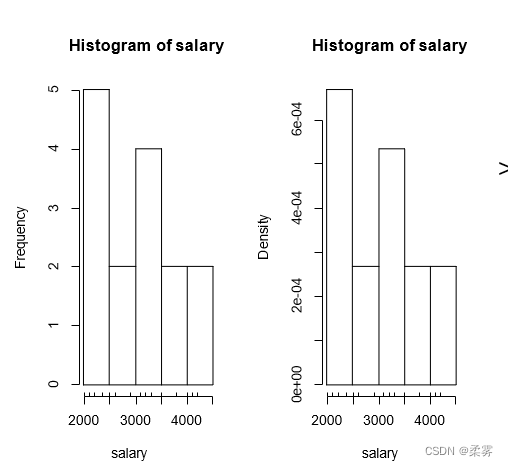
在这里插入图片描述

在R里还可以使用lines(density(x))函数增加核密度估计曲线(plot(density(x)))，结果如下图所示：

lines(density(salary),col="red")

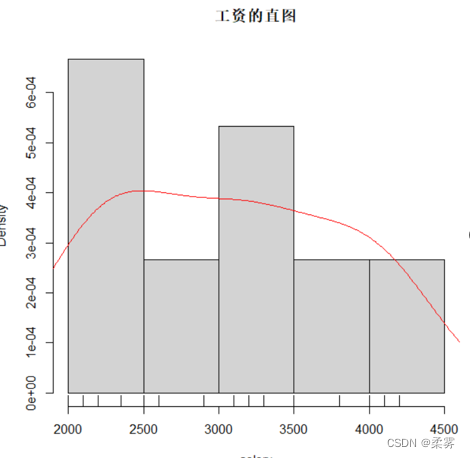
在这里插入图片描述

核密度估计曲线是对数据分布密度的估计，它为数据的分布提了一种平滑的描述，从中可以看出分布的大致形状。

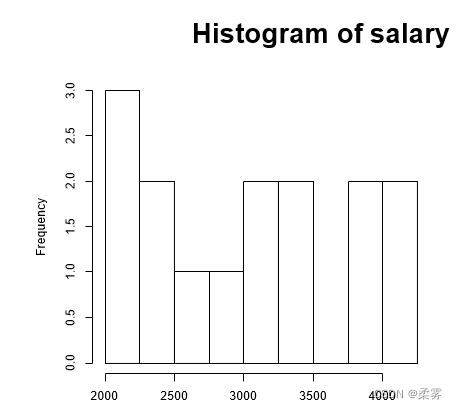
在hist()中还可以指定breaks=n，就可以在直方图中得到大约n个条。还可以指定breaks为一个向量，然后对区间进行分割。

brk=seq(2000,4250,250)#对区间(2000,4250)按每间隔250划分
hist(salary,breaks=brk)

在这里插入图片描述

茎叶图

茎叶图(stem-and-leaf plot)的形状与功能和直方图非常相似，但它是一种文本化的图形。
茎叶图是一种可以较简练地表示数据信息的图表。在茎叶图中,每个数值都被分成两部分，打头的数字作为茎，尾随的数字作为叶。
茎沿竖直轴线放置，叶沿水平轴线堆放。
茎叶图与频数分布类似,但包含了更多信息。

茎叶图它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少。
茎叶图与直方图不同，茎叶图保留原始资料的信息，可以从中统计出次数，计算出各数据段的频率或百分比。从而可以看出分布是否与正态分布或单峰偏态分布逼近。

在数据量不是很大时，茎叶图既显示了完全的原始数据，又显示了数据分布的形状。它像带有长短不一的叶子的茎。
茎叶图优于频数分布的一点是保留了每一个观测对象的真实值。
但是，当数据量很大时，茎叶图就不方便了。
在R软件里用函数stem()作茎叶图。

例题1：
下面一组数据是某生产车间30名工人某日加工零件的个数，请设计适当的茎叶图表示这组数据，并由图出发说明一下这个车间此日的生产情况
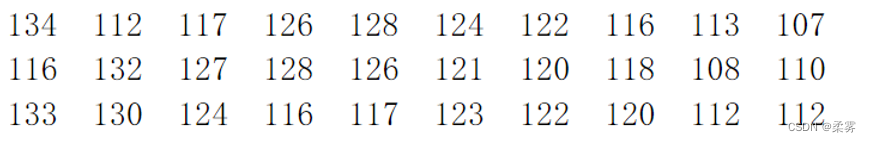
在这里插入图片描述
分析：以前两位数为茎，个位数为叶，可以作出相应的茎叶图，从而可据图分析数据的特征。

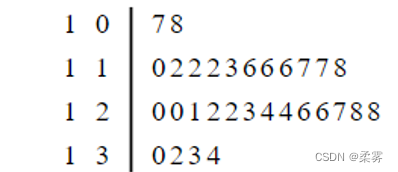
该生产车间的工人加工零件数大多都110到130之间，且分布较对称、集中，说明日生产情况稳定。茎叶图直观地反映了数据的集中趋势

例题2：
甲、乙两个小组各10名学生的英语口语测试成绩如下（单位：分），用茎叶图表示两小组的成绩，并判断哪个小组的成绩更整齐一些。
甲组：76，90，84，86，81，87，86，82，85，83
乙组：82，84，85，89，79，80，91，89，79，74

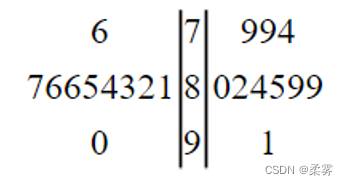
在这里插入图片描述
容易看出甲组成绩较集中，即甲组成绩更整齐一些。
评注：用茎叶图分析数据直观、清晰，所有信息都可以从这个茎叶图中得到。
在R中使用stem.leaf.backback()函数绘制背靠背茎叶图.

例题3：
对工资数据做茎叶图如下：
在这里插入图片描述

stem(salary)

在这里插入图片描述
与直方图相比，茎叶图在反映数据整体分布趋势的同时还能准确反映出具体的数值大小，因此在小样本情况下优势非常明显。

stem(salarym)

在这里插入图片描述
20000 的确是一个异常数据，导致我们不能看清大部分数据的结构。

箱线图

箱线图( Boxplot Graph)是由一个箱子(box)和两条线段(whisker)组成的。
其绘制方法是:先根据上四分位数QU、下四分位数QL和中位数画出中间的箱子，箱子的长度为四分位数间距IQR=QU-QL
对于单组数据，可以绘制简单箱线图；对于多组数据，可以绘制批比较箱线图。
通过箱线图，不仅可以反映出一组数据分布的特征(对称？离群点？)，还可以进行多组数据分布特征的比较。

箱线图上下两条线的长度可以有不同的选择
通常的选择为:如果没有数据值大于QU+1.5×IQR那么该线以数据最大值为端点，否则，线的上端点为上四分位数加上1.5倍的箱子长度，比该端点大的数值则分别在其上方按照其实际值点出。如果数据处于QU +1.5×IQR至 QU+3×IQR的范围内则用圆圈标出，超出了QU+3×IQR 的用星号标出
下面的线也类似。由QL至QL-1.5×IQR区间内的最小值向箱子的底部连线; QL -1.5×IQR至QL -3×IQR的范围内用圆圈标出，小于QL -3×IQR的用星号标出。

单组数据箱线图的一般形式如下图所示：
在这里插入图片描述

通过箱线图的形状，就可以看出数据分布的特征，如下图所示：
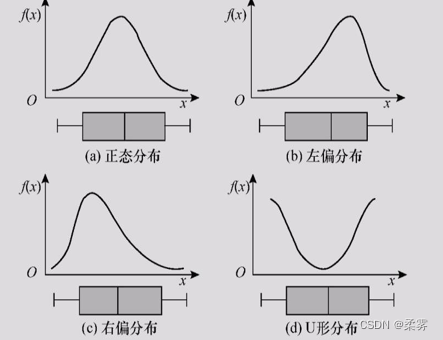
在这里插入图片描述

对称分布的箱线图的特点是：中位数在箱子中间；上下相邻值到箱子的距离等长；离群点在上下内围栏外的分布也大致相同。
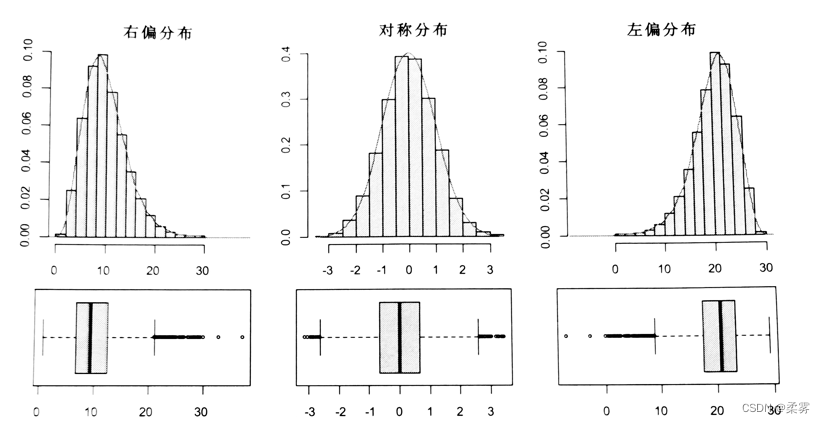
在这里插入图片描述

右偏分布的箱线图的特点是：中位数更靠近25%四分位数的位置；下相邻值到箱子的距离比上相邻值到箱子的距离短；离群点多数在上内围栏之外。
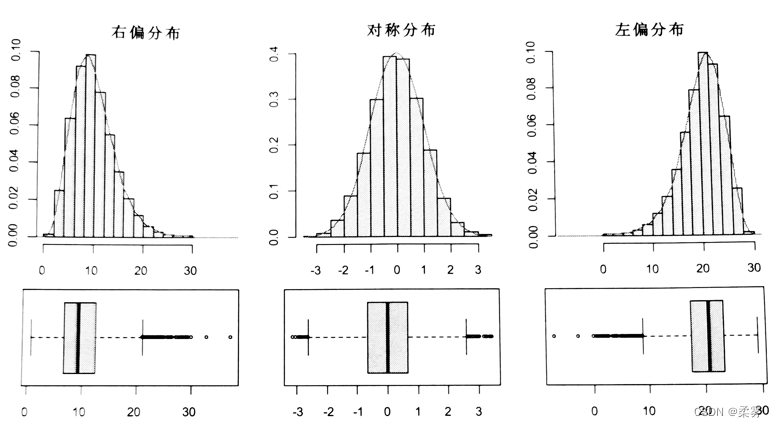
在这里插入图片描述

左偏分布的箱线图的特点是：中位数更靠近75%四分位数的位置；下相邻值到箱子的距离比上相邻值到箱子的距离长；离群点多数在下内围栏之外。
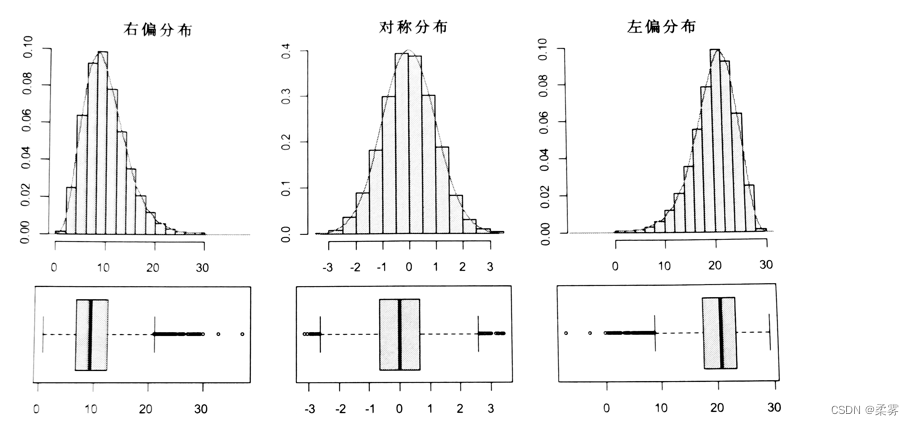
在这里插入图片描述

示例如下：
在R里箱线图的函数是boxplot()，若参数horizontal=F默认为垂直型，
而horizontal=T则为水平型。

par(mfrow=c(1,2))
boxplot(salary)#垂直型
boxplot(salary, horizontal=T)#水平型

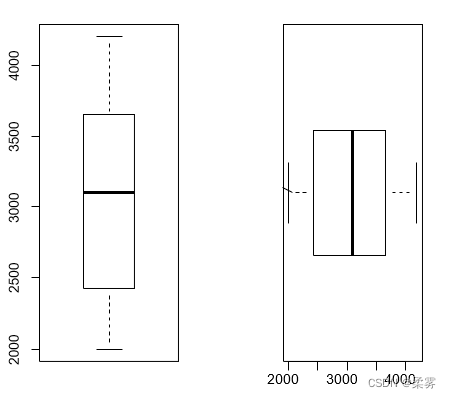
在这里插入图片描述

相对于直方图侧重于对一个连续变量的分布情况进行考察，箱线图更注重于勾勒统计的主要信息，包括最小值最大值、上下四分位数以及中位数，并且适用于对多个连续变量同时考察，或者对一个变量分组进行考察。箱线图使用比较灵活，应用更为广泛
箱线图还可以检验离群值。离群值(outlier)就是明显远离于其他大部分数据某个或少数几个值。
如果观测值距箱线图底线Q1（第25百分位数）或顶线 Q3（第75百分位数）过远，如超出箱体高度（四分位数间距）的1.5倍以上，则可视该观测值为离群值。

示例：
对前面加了经理工资后的月工资数据进行离群值探索，结果如图所示。

boxplot (salarym)

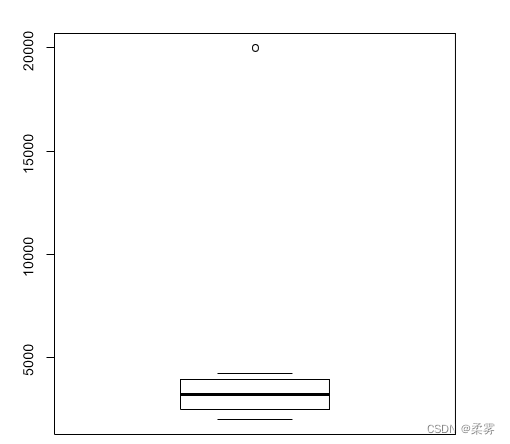
在这里插入图片描述
从图可以看出，该数据有一个离群值，就是经理的工资，远远高于部门其他人的工资，因此被认为是离群值。

练习

1、为分析灯泡的使用寿命（单位：小时），在一批灯泡中随机抽取100只进行测试，得到了一些数据（提供数据exercise2_2，不用自己录入）
（1）绘制直方图和茎叶图，说明数据分布特点

load("C:/Users/86157/Desktop/ch2/exercise2_2.RData")
exercise2_2

直方图

dw<-exercise2_2$灯泡寿命
dw
par(mfrow=c(2,2),cex=0.7,mai=c(0.6,0.6,0.2,0.1))
hist(dw,xlim=c(2700,4200),ylim=c(0,30),labels=T,xlab ="灯泡寿命",ylab="频数",main="(a)直方图1")#每一条上方标注频数
rug(dw)
hist(dw,freq=FALSE,breaks=20,xlab="灯泡寿命",ylab="密度",main="直方图2",col="pink")
lines(density(dw),col="red")