1. 伸长张量与Cauchy-Green 张量

由于变形梯度为正则仿射量，故可进行极分解:
$$\mathbf{F}=\mathbf{R}\cdot \mathbf{U}=\mathbf{V}\cdot \mathbf{R}$$
将正交仿射量 $\mathbf{R}$ 称作转动张量；正张量 $\mathbf{U}$、$\mathbf{V}$ 分别称作 右、左伸长张量，且满足：
$$\begin{gathered} \mathbf{U}=\sqrt{{\mathbf{F}}^{\mathbf{T}}\cdot \mathbf{F}} \\ \mathbf{V}=\sqrt{\mathbf{F}\cdot {\mathbf{F}}^{\mathbf{T}}} \\ \mathbf{U}={\mathbf{R}}^{\mathbf{T}}\cdot \mathbf{V}\cdot \mathbf{R} \end{gathered}$$
上述极分解的物理意义可以理解为：
$$d\vec{x}=\mathbf{F}\cdot d\vec{X}=\mathbf{R}\cdot (\mathbf{U}\cdot d\vec{X})=\mathbf{V}\cdot (\mathbf{R}\cdot d\vec{X})$$
即，参考构型的线元到当前构型中的线元的映射既可以是先进行旋转再进行左伸长仿射量对应的变换也可以是先进行右伸长张量对应的变换再进行旋转操作。

进一步可以定义：
$$\begin{array}{rl}& \mathbf{C}\triangleq {\mathbf{U}}^2={\mathbf{F}}^{\mathbf{T}}\cdot \mathbf{F}=({\vec{C}}_A\otimes {\vec{G}}^A{)}^T\cdot ({\vec{C}}_B\otimes {\vec{G}}^B)=C_{AB}{\vec{G}}^A\otimes {\vec{G}}^B\\ & \\ & =({\vec{g}}_j\otimes \vec{c}{}^j{)}^T\cdot ({\vec{g}}_i\otimes \vec{c}{}^i)=g_{ji}\vec{c}{}^j\otimes \vec{c}{}^i\\ & \\ & \mathbf{B}\triangleq {\mathbf{V}}^2=\mathbf{F}\cdot {\mathbf{F}}^{\mathbf{T}}=({\vec{g}}_i\otimes \vec{c}{}^i)\cdot ({\vec{g}}_j\otimes \vec{c}{}^j{)}^T=\stackrel{-1}{c}{}^{ij}{\vec{g}}_i\otimes {\vec{g}}_j\triangleq \stackrel{-1}{\mathbf{c}}\\ & \\ & =({\vec{C}}_B\otimes {\vec{G}}^B)\cdot ({\vec{C}}_A\otimes {\vec{G}}^A{)}^T=G^{BA}{\vec{C}}_B\otimes {\vec{C}}_A\end{array}$$
$\mathbf{C}$ 与 $\mathbf{B}$ 分别称作右、左 Cauchy-Green 张量，二者间满足：
$$\mathbf{C}={\mathbf{R}}^{\mathbf{T}}\cdot \mathbf{B}\cdot \mathbf{R}(正交相似关系)$$
说明，二者具有相同的特征值: ${\lambda }_C={\lambda }_B=\lambda$，特征方向仅相差一个刚性转动: ${\vec{u}}_C={\mathbf{R}}^T\cdot {\vec{u}}_B$。另外，它们都是对称正定仿射量，是正则的，其逆分别为：
$$\begin{array}{rl}& \stackrel{-1}{\mathbf{C}}=({\mathbf{U}}^2{)}^{-1}=\stackrel{-1}{\mathbf{F}}\cdot \stackrel{-\mathbf{T}}{\mathbf{F}}=({\vec{G}}_A\otimes {\vec{C}}^A)\cdot ({\vec{G}}_B\otimes {\vec{C}}^B{)}^T=\stackrel{-1}{C}{}^{AB}{\vec{G}}_A\otimes {\vec{G}}_B\\ & \\ & =({\vec{c}}_j\otimes {\vec{g}}^j)\cdot ({\vec{c}}_i\otimes {\vec{g}}^i{)}^T=g^{ji}{\vec{c}}_j\otimes {\vec{c}}_i\\ & \\ & \stackrel{-1}{\mathbf{B}}=({\mathbf{V}}^2{)}^{-1}=\stackrel{-\mathbf{T}}{\mathbf{F}}\cdot \stackrel{-1}{\mathbf{F}}=({\vec{c}}_i\otimes {\vec{g}}^i{)}^T\cdot ({\vec{c}}_j\otimes {\vec{g}}^j)=c_{ij}{\vec{g}}^i\otimes {\vec{g}}^j\triangleq \mathbf{c}\\ & \\ & =({\vec{G}}_A\otimes {\vec{C}}^A{)}^T\cdot ({\vec{G}}_B\otimes {\vec{C}}^B)=G_{AB}{\vec{C}}^A\otimes {\vec{C}}^B\end{array}$$

2. 线元长度的改变

2.1. 初始/当前构型下的长度比

设参考构型中 A 点邻域内的有向线元 $d\vec{X}$ 的长度为 $d{s}_0$；经过运动变形后，A 点映射为当前构型中的 A’ 点而 $d\vec{X}$ 映射为其邻域内的有向线元 $d\vec{x}$ ，长度为 $ds$，满足：
$$\{\begin{array}{l}d{s}_0^2=d\vec{X}\cdot d\vec{X}=(d\vec{x}\cdot \stackrel{-\mathbf{T}}{\mathbf{F}})\cdot (\stackrel{-1}{\mathbf{F}}\cdot d\vec{x})=d\vec{x}\cdot \mathbf{c}\cdot d\vec{x}=d\vec{x}\cdot \stackrel{-1}{\mathbf{B}}\cdot d\vec{x}\\ \\ d{s}^2=d\vec{x}\cdot d\vec{x}=(d\vec{X}\cdot {\mathbf{F}}^T)\cdot (\mathbf{F}\cdot d\vec{X})=d\vec{X}\cdot \mathbf{C}\cdot d\vec{X}\end{array}$$
令
$$\{\begin{array}{l}\vec{L}\triangleq \frac{d\vec{X}}{|d\vec{X}|}=L^i{\vec{G}}_i\\ \\ \vec{l}\triangleq \frac{d\vec{x}}{|d\vec{x}|}=l^i{\vec{g}}_i\end{array}$$
将 $\vec{L}、\vec{l}$ 分别称作变形前任意有向线元 $d\vec{X}$ 与变形后任意有向线元 $d\vec{x}$ 的单位切向量。

将变形前位于 $\vec{L}$ 方向的线元历经变形、运动前后的长度比定义为：
$${\lambda }_L\triangleq \frac{ds}{d{s}_0}={\left(\frac{d\vec{X}\cdot \mathbf{C}\cdot d\vec{X}}{|d\vec{X}|\cdot |d\vec{X}|}\right)}^{\frac{1}{2}}=(\vec{L}\cdot \mathbf{C}\cdot \vec{L}{)}^{\frac{1}{2}}=(L^A{L}^B{C}_{AB}{)}^{\frac{1}{2}}(物质坐标系下的分量)$$
将变形后位于 $\vec{l}$ 方向的线元历经变形、运动前后的长度比定义为：
$${\lambda }_l\triangleq \frac{ds}{d{s}_0}={\left(\frac{|d\vec{x}|\cdot |d\vec{x}|}{d\vec{x}\cdot \mathbf{c}\cdot d\vec{x}}\right)}^{\frac{1}{2}}=(\vec{l}\cdot \mathbf{c}\cdot \vec{l}{)}^{-\frac{1}{2}}=(l^r{l}^s{c}_{rs}{)}^{-\frac{1}{2}}(空间坐标系下的分量)$$
显然，当变形前位于 $\vec{L}$ 方向的线元经历变形、运动后位于 $\vec{l}$ 方向时有：
$${\lambda }_L={\lambda }_l$$

2.2. 主长度比与 Lagrange/Euler 主方向

此外，根据其定义可知：长度比是一个与方向相关的物理量，针对于参考构型/当前构型中同一点而言，不同方向的长度比不同。自然地会问：什么方向上长度比最大？即求解如下带约束的极值问题：
$$\{\begin{array}{l}\underset{\vec{L}}{\max }{\lambda }_L(\vec{L})\\ \\ |{\vec{L}}_{|}=1\end{array}和\{\begin{array}{l}\underset{\vec{l}}{\max }{\lambda }_l(\vec{l})\\ \\ |\vec{l}|=1\end{array}$$
注意到长度比恒为正，为简化计算，将上述极值问题等价于求解：
$$\{\begin{array}{l}\underset{\vec{L}}{\max }{\lambda }_L^2(\vec{L})\\ \\ |\vec{L}|=1\end{array}和\{\begin{array}{l}\underset{\vec{l}}{\max }{\lambda }_l^2(\vec{l})\\ \\ |\vec{l}|=1\end{array}$$
以前一个极值问题的求解为例，采用 Lagrange 乘子法进行求解，使得问题化为如下无约束极值问题的必要条件：
$$\{\begin{array}{l}\frac{\partial }{\partial L^M}\left[L^A{L}^B{C}_{AB}-\eta (L^A{L}^B{G}_{AB}-1)\right]=0(M=1,2,3)\\ \\ L^A{L}^B{G}_{AB}-1=0\end{array}$$
即
$$\{\begin{array}{l}(C_{AM}-\eta G_{AM})L^A=0(M=1,2,3)\\ \\ L^A{L}^B{G}_{AB}-1=0\end{array}⟹\{\begin{array}{l}(C_{\bullet M}^A-\eta {\delta }_{\bullet M}^A)L_A=0(M=1,2,3)\\ \\ L^A{L}^B{G}_{AB}-1=0\end{array}$$
注意到：$C_{AB}$ 不仅是右 Cauchy-Green 张量在物质坐标系下的协变分量，同时也是随体坐标系 {XA,t}\{X^A,t\}{XA,t} 度量张量的协变分量，但上述指标升降是通过物质坐标系下的度量张量协变、逆变分量实现的，因此 $C_{\bullet M}^A\ne {\delta }_{\bullet M}^A$。

上述四元 非线性(约束条件) 方程组的求解等价于求右 Cauchy-Green 张量的特征值问题 ：
$$(\mathbf{C}-\eta \mathbf{I})\cdot \vec{L}=0$$
由于 $\mathbf{C}$ 为对称正定张量，故存在三个正特征值 ${\eta }_{\alpha }\triangleq {\lambda }_{\alpha }^2>0(\alpha =1,2,3)$ 和相应的三个两两垂直的单位特征向量 ${\vec{L}}_{\alpha }$。

从上述讨论可知：于初始构型上的某点而言，该点右Cauchy-Green 张量 (右伸长张量 U) 的特征方向是该点变形、运动前后长度比达到极大/小或驻值的方向，将其称作 Lagrange 主方向。Lagrange 主方向上的长度比为：
$${\lambda }_{L_{\alpha }}=\sqrt{{\vec{L}}_{\alpha }\cdot \mathbf{C}\cdot {\vec{L}}_{\alpha }}=\sqrt{{\lambda }_{\alpha }^2{\vec{L}}_{\alpha }\cdot {\vec{L}}_{\alpha }}={\lambda }_{\alpha }$$
即，Lagrange 主方向上的长度比为该右Cauchy-Green 张量 C 特征方向对应特征值的算数平方根(右伸长张量 U 的特征值)，将其称作 主长度比。

同理，求解后一极值问题等价于求解左 Cauchy-Green 张量的逆 $\mathbf{c}$ 的特征值问题：
$$(\mathbf{c}-{\eta }^{\prime }\mathbf{I})\cdot \vec{l}=0$$
其中，$\mathbf{g}$ 为空间坐标系的度量张量。类似的，$\mathbf{c}$ 也存在三个正特征值 ${\eta }_{\alpha }^{\prime }\triangleq \frac{1}{{{\lambda }_{\alpha }^{\prime }}^2}>0(\alpha =1,2,3)$和相应的三个两两垂直的单位特征向量 ${\vec{l}}_{\alpha }$。由于左、右 Cauchy-Green 张量具有相同的特征值，故
$${\eta }_{\alpha }^{\prime }=\frac{1}{{\eta }_{\alpha }}=\frac{1}{{{\lambda }_{\alpha }}^2}$$
又由于左、右 Cauchy-Green 张量的特征方向仅相差一转动张量 $\mathbf{R}$，且正则仿射量与其逆同特征方向，则
$${\vec{L}}_{\alpha }={\mathbf{R}}^T\cdot {\vec{l}}_{\alpha }(\ast )$$
上述讨论说明对于当前构型上的某点，其左Cauchy-Green 张量或其逆 (或左伸长张量 V) 的特征方向是该点变形、运动前后长度比达到极大/小或驻值的方向，将其称作 Euler 主方向。Euler 主方向上的长度比为：
$${\lambda }_{l_{\alpha }}=\frac{1}{\sqrt{{\vec{l}}_{\alpha }\cdot \mathbf{c}\cdot {\vec{l}}_{\alpha }}}=\frac{{\lambda }_{\alpha }}{\sqrt{{\vec{l}}_{\alpha }\cdot {\vec{l}}_{\alpha }}}={\lambda }_{\alpha }$$
即，Euler 主方向上的长度比为该左Cauchy-Green 张量 B 特征方向对应的特征值的算数平方根 (左伸长张量 V 的特征值)。且 Euler 主方向上的长度比与 Lagrange 主方向上的长度比 分别一 一对应相等，即 ${\lambda }_{L_{\alpha }}={\lambda }_{l_{\alpha }}={\lambda }_{\alpha }$。

2.3. 初始/当前构型下任意方向的长度比

根据谱分解，左、右伸长张量，左、右 Cauchy-Green 张量，变形梯度张量及其逆可通过 Euler 主方向/ Lagrange 主方向 与主长度比进行表示，即：
$$\begin{array}{rl}& \{\begin{array}{l}\mathbf{U}=\sum _{\alpha =1}^3{\lambda }_{\alpha }{\vec{L}}_{\alpha }\otimes {\vec{L}}_{\alpha }\\ \\ \mathbf{V}=\sum _{\alpha =1}^3{\lambda }_{\alpha }{\vec{l}}_{\alpha }\otimes {\vec{l}}_{\alpha }\end{array}\\ & \\ & \{\begin{array}{l}\mathbf{C}=\sum _{\alpha =1}^3{\lambda }_{\alpha }^2{\vec{L}}_{\alpha }\otimes {\vec{L}}_{\alpha }\\ \\ \mathbf{B}=\sum _{\alpha =1}^3{\lambda }_{\alpha }^2{\vec{l}}_{\alpha }\otimes {\vec{l}}_{\alpha }，\mathbf{c}={\mathbf{B}}^{-1}=\sum _{\alpha =1}^3\frac{1}{{\lambda }_{\alpha }^2}{\vec{l}}_{\alpha }\otimes {\vec{l}}_{\alpha }\end{array}\end{array}$$
由于，转动张量也可通过主方向进行表示
$$\mathbf{R}=\sum _{\alpha =1}^3{\vec{l}}_{\alpha }\otimes {\vec{L}}_{\alpha }$$
则有：
$$\begin{gathered} \mathbf{F}=\mathbf{V}\cdot \mathbf{R}=\mathbf{R}\cdot \mathbf{U}=\sum _{\alpha =1}^3{\lambda }_{\alpha }{\vec{l}}_{\alpha }\otimes {\vec{L}}_{\alpha } \\ {\mathbf{F}}^{-1}={\mathbf{R}}^{\mathbf{T}}\cdot {\mathbf{V}}^{-1}={\mathbf{U}}^{-1}\cdot {\mathbf{R}}^{\mathbf{T}}=\sum _{\alpha =1}^3\frac{1}{{\lambda }_{\alpha }}{\vec{L}}_{\alpha }\otimes {\vec{l}}_{\alpha } \end{gathered}$$

• 对于参考构型中某点具有任意单位切向量 $\vec{M}=M^{\alpha }{\vec{L}}_{\alpha }$ 的有向线元而言，其伸长比为：
  $${\lambda }_M=(\vec{M}\cdot \mathbf{C}\cdot \vec{M}{)}^{\frac{1}{2}}={\left[\sum _{\alpha =1}^3(M^{\alpha }{\vec{L}}_{\alpha })\cdot \sum _{i=1}^3\left({\lambda }_i^2{\vec{L}}_i\otimes {\vec{L}}_i\right)\cdot \sum _{\beta =1}^3(M^{\beta }{\vec{L}}_{\beta })\right]}^{\frac{1}{2}}={\left[\sum _{\alpha =1}^3({\lambda }_{\alpha }{M}^{\alpha }{)}^2\right]}^{\frac{1}{2}}(不对\alpha 、\beta 求和)$$
  其中， $M^{\alpha }$ 为参考构型下任意单位切向量 $\vec{M}$ 在 Lagrange主方向下 的分量。

• 对于当前构型中某点具有任意单位切向量 $\vec{m}=m^{\alpha }{\vec{l}}_{\alpha }$ 的有向线元而言，其伸长比为：
  $${\lambda }_m=(\vec{m}\cdot \mathbf{c}\cdot \vec{m}{)}^{-\frac{1}{2}}={\left[\sum _{\alpha =1}^3(m^{\alpha }{\vec{l}}_{\alpha })\cdot \sum _{i=1}^3\left(\frac{1}{{\lambda }_i^2}{\vec{l}}_i\otimes {\vec{l}}_i\right)\cdot \sum _{\beta =1}^3(m^{\beta }{\vec{l}}_{\beta })\right]}^{-\frac{1}{2}}={\left[\sum _{\alpha =1}^3{\left(\frac{m^{\alpha }}{{\lambda }_{\alpha }}\right)}^2\right]}^{-\frac{1}{2}}(不对\alpha 、\beta 求和)$$
  其中， $m^{\alpha }$ 为当前构型下任意单位切向量 $\vec{m}$ 在 Euler主方向下 的分量。

3. 线元夹角的改变

下图为变形前后两线元的夹角变化过程：

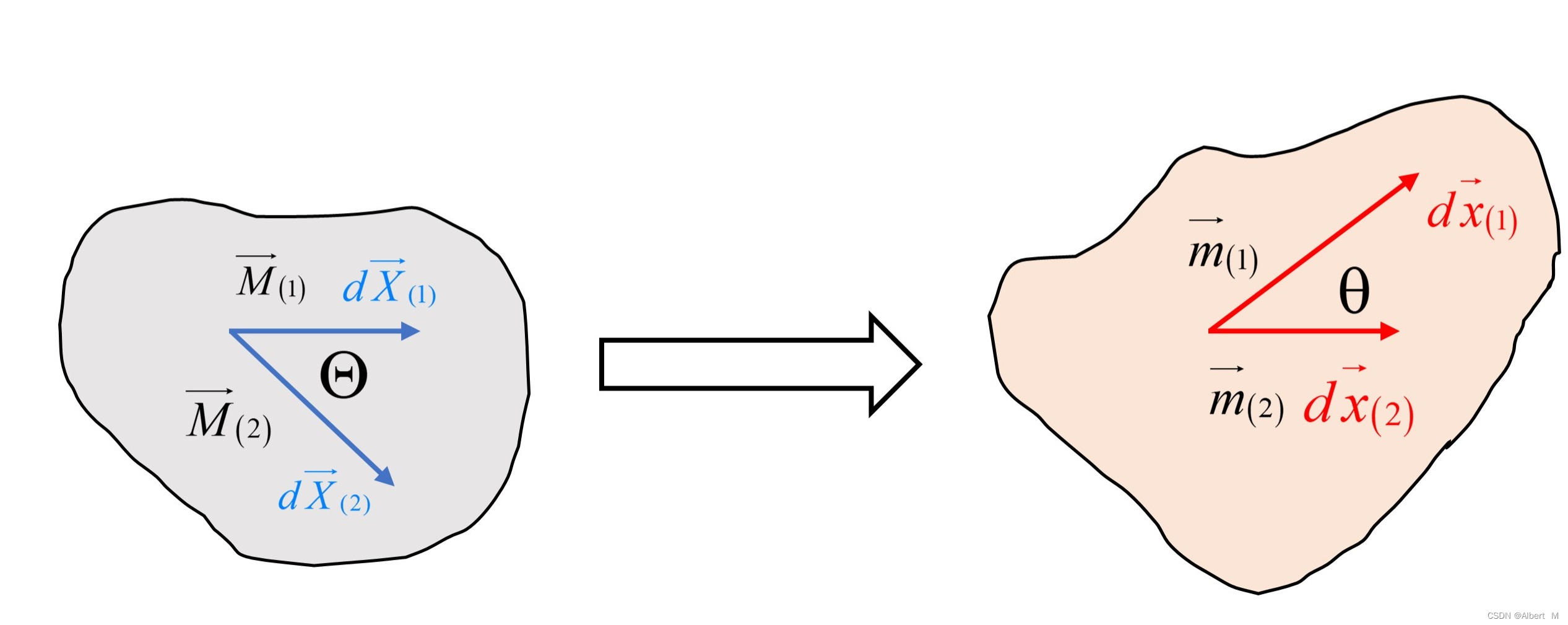
则变形前、后两线元的夹角余弦分别为：
$$\begin{gathered} cos\Theta ={\vec{M}}_{(1)}\cdot {\vec{M}}_{(2)}=\frac{d{\vec{X}}_{(1)}\cdot d{\vec{X}}_{(2)}}{|d{\vec{X}}_{(1)}|\cdot |d{\vec{X}}_{(2)}|} \\ cos\theta ={\vec{m}}_{(1)}\cdot {\vec{m}}_{(2)}=\frac{d{\vec{x}}_{(1)}\cdot d{\vec{x}}_{(2)}}{|d{\vec{x}}_{(1)}|\cdot |d{\vec{x}}_{(2)}|} \end{gathered}$$
又
$$\begin{array}{rl}& d{\vec{x}}_{(1)}=\mathbf{F}\cdot d{\vec{X}}_{(1)}，d{\vec{X}}_{(1)}=\stackrel{-1}{\mathbf{F}}\cdot d{\vec{x}}_{(1)}\\ & \\ & d{\vec{x}}_{(2)}=\mathbf{F}\cdot d{\vec{X}}_{(2)}，d{\vec{X}}_{(2)}=\stackrel{-1}{\mathbf{F}}\cdot d{\vec{x}}_{(2)}\\ & \\ & |d{\vec{x}}_{(1)}|={\lambda }_{m_{(1)}}|d{\vec{X}}_{(1)}|={\lambda }_{M_{(1)}}|d{\vec{X}}_{(1)}|\\ & \\ & |d{\vec{x}}_{(2)}|={\lambda }_{m_{(2)}}|d{\vec{X}}_{(2)}|={\lambda }_{M_{(2)}}|d{\vec{X}}_{(1)}|\end{array}$$

• 那么，当立足于初始构型，若已知任意两方向，其夹角为 $\Theta$，那么经过变形后两方向的夹角余弦为：
  $$cos\theta =\frac{d{\vec{x}}_{(1)}\cdot d{\vec{x}}_{(2)}}{|d{\vec{x}}_{(1)}|\cdot |d{\vec{x}}_{(2)}|}=\frac{1}{{\lambda }_{M_{(1)}}{\lambda }_{M_{(2)}}}\frac{d{\vec{X}}_{(1)}\cdot \mathbf{C}\cdot d{\vec{X}}_{(2)}}{|d{\vec{X}}_{(1)}||d{\vec{X}}_{(2)}|}=\frac{1}{{\lambda }_{M_{(1)}}{\lambda }_{M_{(2)}}}({\vec{M}}_{(1)}\cdot \mathbf{C}\cdot {\vec{M}}_{(2)})$$
  进一步，
  $$cos\theta =\frac{1}{{\lambda }_{M_{(1)}}{\lambda }_{M_{(2)}}}\left[\sum _{\alpha =1}^3(M_{(1)}^{\alpha }{\vec{L}}_{\alpha })\cdot \sum _{i=1}^3\left({\lambda }_i^2{\vec{L}}_i\otimes {\vec{L}}_i\right)\cdot \sum _{\beta =1}^3(M_{(2)}^{\beta }{\vec{L}}_{\beta })\right]=\frac{1}{{\lambda }_{M_{(1)}}{\lambda }_{M_{(2)}}}\sum _{\alpha =1}^3({\lambda }_{\alpha }^2{M}_{(1)}^{\alpha }{M}_{(2)}^{\alpha })$$
  其中， $M_{(1)}^{\alpha }、M_{(2)}^{\alpha }$ 为参考构型下两任意单位切向量 ${\vec{M}}_{(1)}、{\vec{M}}_{(2)}$ 分别在 Lagrange主方向下 的分量，${\lambda }_{\alpha }$ 为主长度比。

• 另外，若立足于当前构型，若已知任意两方向，其夹角为 $\theta$，那么经历变形前两方向的夹角余弦为：
  $$cos\Theta =\frac{d{\vec{X}}_{(1)}\cdot d{\vec{X}}_{(2)}}{|d{\vec{X}}_{(1)}|\cdot |d{\vec{X}}_{(2)}|}=({\lambda }_{m_{(1)}}{\lambda }_{m_{(2)}})\frac{d{\vec{x}}_{(1)}\cdot \mathbf{c}\cdot d{\vec{x}}_{(2)}}{|d{\vec{x}}_{(1)}||d{\vec{x}}_{(2)}|}=({\lambda }_{m_{(1)}}{\lambda }_{m_{(2)}})({\vec{m}}_{(1)}\cdot \mathbf{c}\cdot {\vec{m}}_{(2)})$$
  进一步，
  $$cos\Theta ={\lambda }_{m_{(1)}}{\lambda }_{m_{(2)}}\left[\sum _{\alpha =1}^3(m_{(1)}^{\alpha }{\vec{l}}_{\alpha })\cdot \sum _{i=1}^3\left(\frac{1}{{\lambda }_i^2}{\vec{l}}_i\otimes {\vec{l}}_i\right)\cdot \sum _{\beta =1}^3(m_{(2)}^{\beta }{\vec{l}}_{\beta })\right]=({\lambda }_{m_{(1)}}{\lambda }_{m_{(2)}})\sum _{\alpha =1}^3\left(\frac{1}{{\lambda }_{\alpha }^2}{m}_{(1)}^{\alpha }{m}_{(2)}^{\alpha }\right)$$
  其中， $m_{(1)}^{\alpha }、m_{(2)}^{\alpha }$ 为参考构型下两任意单位切向量 ${\vec{m}}_{(1)}、{\vec{m}}_{(2)}$ 分别在 Euler主方向下 的分量，${\lambda }_{\alpha }$ 为主长度比。

4. 面元的改变

面元可通过如下的向量给出它的几何特征，向量的方向代表面元的单位法向量，向量的模代表面元的大小。则参考构型与当前构型下的平行四边形面元分别为：
$$\{\begin{array}{l}{}_0\vec{N}d{S}_0=d{\vec{X}}_{(1)}\times d{\vec{X}}_{(2)}\\ \\ \vec{N}dS=d{\vec{x}}_{(1)}\times d{\vec{x}}_{(2)}\end{array}$$
其中，${}_0\vec{N}、\vec{N}$ 分别为变形前后面元的单位法向量，$d{S}_0、dS$ 分别为变形前后面元的大小。

那么，根据 Nanson 公式：
$$\vec{N}dS=(\mathbf{F}\cdot d{\vec{X}}_{(1)})\times (\mathbf{F}\cdot d{\vec{X}}_{(2)})=det(\mathbf{F})\stackrel{-\mathbf{T}}{\mathbf{F}}\cdot (d{\vec{X}}_{(1)}\times d{\vec{X}}_{(2)})=\mathcal{J}\stackrel{-\mathbf{T}}{\mathbf{F}}\cdot {}_0\vec{N}d{S}_0$$
由于任何形状的面元均可通过无穷多个平行四边形来近似，故上述针对平行四边形面元的变换关系对于任意形状的面元也成立。

5. 体元的改变

参考/当前构型中的平行六面体的微元的体积分别为：
$$\{\begin{array}{l}d{v}_0=|d{\vec{X}}_1\cdot (d{\vec{X}}_2\times d{\vec{X}}_3)|\\ \\ dv=|d{\vec{x}}_1\cdot (d{\vec{x}}_2\times d{\vec{x}}_3)|\end{array}$$
那么,
$$\begin{array}{rl}& dv=|d{\vec{x}}_1\cdot (d{\vec{x}}_2\times d{\vec{x}}_3)|\\ & \\ & =|(\mathbf{F}\cdot d{\vec{X}}_1)\cdot [(\mathbf{F}\cdot d{\vec{X}}_2)\times (\mathbf{F}\cdot d{\vec{X}}_3)]|\\ & \\ & =|det(\mathbf{F})||d{\vec{X}}_1\cdot (d{\vec{X}}_2\times d{\vec{X}}_3)|\\ & \\ & =|\mathcal{J}|d{v}_0=\mathcal{J}d{v}_0\\ & \\ & =|det(\mathbf{R})||det(\mathbf{U})|d{v}_0\\ & \\ & =\left(\prod _{\alpha =1}^3{\lambda }_{\alpha }\right)d{v}_0\end{array}$$
其中，${\lambda }_{\alpha }（\alpha =1,2,3）$ 为主长度比

由于任意形状的体元可以用无穷个多个平行六面体的逼近，故上述平行六面体体元间的映射关系对于任意形状的体元也是成立的。

对于 等容变形 应有：
$$\mathcal{J}=1$$
因此，有时也将变形梯度分解为等容部分与体积部分的乘积，其中等容部分定义为
$$\hat{\mathbf{F}}\triangleq {\mathcal{J}}^{-\frac{1}{3}}\mathbf{F}$$
显然，
$$det(\hat{\mathbf{F}})=1$$
则，
$$\mathbf{F}=\hat{\mathbf{F}}\cdot ({\mathcal{J}}^{\frac{1}{3}}\mathbf{G})$$
显然，体积部分 ${\mathcal{J}}^{\frac{1}{3}}\mathbf{G}$ 是球形张量（各向同性张量）。