一、题目描述

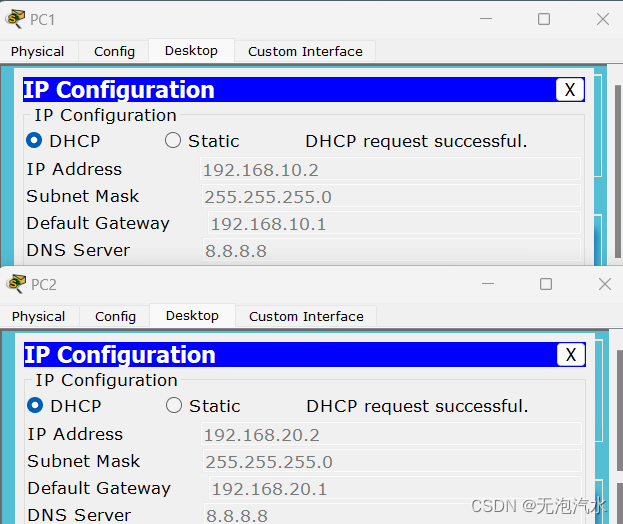
P8754 [蓝桥杯 2021 省 AB2] 完全平方数

二、问题简析

2.1 唯一分解定理

唯一分解定理：大于1的自然数都可以唯一地写成素数的积。

由该定理，一个大于 $1$ 的自然数 $b$ 可以表示为 $b=a_1^{p_1}\ast a_2^{p_2}\ast ...\ast a_n^{p_n}$ ($a_1,a_2,...,a_n$ 为素数；$p_1,p_2,...,p_n$ 为对应的指数，即有 $p_n$ 个该数)。该自然数 $b$ 的平方为 $b^2=a_1^{2p_1}\ast a_2^{2p_2}\ast ...\ast a_n^{2p_n}$，所有的指数都是偶数。
我们可以得到，若一个自然数是完全平方数，则将该自然数写出素数的积后，每个素数的指数一定是偶数。

因此，我们可以分解 $n$，将指数不为偶数的素数相乘，就得到了 $x$。

2.2 分解自然数

以下代码给出了如何将大于 $1$ 的自然数分解为素数的积。

// 将整数n分解成若干个素数，除1和本身
map<int, int> factors(int n)
{map<int, int> ans;      // 分解n后，有ans[i]个i// n==1，特殊考虑if (n == 1){ans[n] = 1;return ans;}// 1和本身总是因数，这里忽略for (int i = 2; i * i <= n; i++){// 可能有若干个iwhile (n % i == 0){ans[i]++;       // 分解出一个in /= i;}}if (n != 1)             // n==1，已经分解完了ans[n] += 1;return ans;
}

---

三、AC代码

#include <bits/stdc++.h>using namespace std;
typedef long long ll;int quickin(void)
{int ret = 0;bool flag = false;char ch = getchar();while (ch < '0' || ch > '9'){if (ch == '-')    flag = true;ch = getchar();}while (ch >= '0' && ch <= '9' && ch != EOF){ret = ret * 10 + ch - '0';ch = getchar();}if (flag)    ret = -ret;return ret;
}int main()
{#ifdef LOCALfreopen("test.in", "r", stdin);#endifll n, ans = 1;cin >> n;if (n == 1){cout << 4 << endl;return 0;	}for (ll i = 2; i * i <= n; i++){ll cnt = 0;while (n % i == 0){cnt += 1;n /= i;	}if (cnt % 2 != 0)    ans *= i;}if (n != 1)    ans *= n;cout << ans << endl;return 0;
}

---

完