算法与数据结构之间存在密不可分的关系。简单来说,数据结构是存储和组织数据的方式,而算法则是操作和处理这些数据的方法。
首先,数据结构为算法提供了基础。算法是解决问题的步骤和流程,通过对数据结构进行操作,算法可以实现对数据的增删改查等操作。不同的数据结构特性影响算法的操作方式,例如,如果算法需要对一个有序数组进行搜索,那么它需要知道数组的有序性质,以便采用二分搜索的方式进行操作。同时,对于同一问题,不同的数据结构可能会导致不同的算法实现方式,因此在选择数据结构时必须考虑算法的复杂度和效率。
其次,算法对数据结构的优化和选择也有重要影响。算法可以通过优化数据结构来提高其性能,例如,通过使用合适的排序算法,可以减少排序时间。反过来,数据结构的设计也需要考虑到算法的实现和运行效率。一些排序算法需要随机访问数组元素,而另一些算法则需要在不同的时间点插入和删除元素,这些需求都会影响数据结构的选择。
程序= 数据结构+算法
算法的五个重要特性包括:
- 有穷性:算法必须能在执行有限个步骤之后终止。也就是说,一个算法在执行过程中不能无限循环,每个步骤都应该在有限时间内完成。
- 确切性:算法的每一步骤必须有确切的定义,不能有二义性。这意味着算法的每一步都是清晰、明确的,不存在模糊或不确定的地方。
- 输入:一个算法有0个或多个输入,以刻画运算对象的初始情况。这些输入是算法开始执行前所必需的,它们为算法提供了初始数据和条件。
- 输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果。输出是算法执行完毕后得到的结果,是算法的主要目的。
- 可行性:算法中执行的任何计算步骤都应该是可以执行的,即每个计算步都可以在有限时间内完成。这意味着算法所描述的操作都是实际可行的,可以通过已经实现的基本操作执行有限次来实现。
算法设计要求:
- 正确性与健壮性:
- 算法必须能够准确执行其预定功能,对于所有合法的输入都能产生正确的输出结果。
- 算法应当具有健壮性,即能够合理处理异常情况、错误输入或非法数据,并给出相应的提示或处理结果,确保算法的稳定性和可靠性。
- 可读性:
- 算法设计应易于阅读和理解,使用清晰、简洁的语言和符号表达算法的逻辑。
- 算法的结构应合理,逻辑应清晰,方便他人理解算法的工作原理和实现过程,便于后续的调试、维护和升级。
- 效率:
- 算法设计应追求高效,包括时间效率和空间效率。
- 在满足正确性的前提下,应尽量减少算法的执行时间和所需的存储空间,提高算法的性能。
- 可以通过优化算法的时间复杂度和空间复杂度来实现高效的算法设计。
- 可维护性:
- 算法设计应考虑可维护性,使算法易于修改和扩展。
- 算法应具有模块化和结构化的特点,便于对各个部分进行单独的修改和替换。
- 同时,算法的设计应考虑到未来的变化和升级需求,能够方便地添加新功能或修改现有功能,以适应不同的应用场景和需求。
算法时间效率的度量:
算法的时间效率可以依据算法编制的程序在计算机上执行进行的消耗的时间来度量。
1.事后统计:要求将算法编程程序(计算机的软硬件会影响算法的优劣)
2.事前分析:只能进行估算(更多用这个)
算法时间 = Σ每条语句频度*该语句执行一次的所需时间
假设每条语句执行的所需的时间均为单位时间,所以对算法运行时间就转化为讨论算法中所有语句执行次数,也就是频度之和。
例:
for(i=1;i<=n;i++){for(j=1;j<=n;j++){c[i][j]=0;for(k=0;k<n;k++)c[i][j]=c[i][j]+a[i][k]*b[i][k];}这个代码段包含三个嵌套的循环,用于计算一个二维数组
c的元素,其中c[i][j]是通过矩阵乘法得到的,即c[i][j]是由矩阵a的第i行与矩阵b的第j列的点积计算得出的。首先,我们来分析每个循环的迭代次数:
- 外层循环
i迭代n次(从1到n)。- 中层循环
j也在每次外层循环i的迭代中迭代n次(从1到n)。- 内层循环
k在每次中层循环j的迭代中迭代n次(从0到n-1)。因此,总的迭代次数是
n(外层循环)*n(中层循环)*n(内层循环)=n^3。由于内层循环中的操作(即
c[i][j]=c[i][j]+a[i][k]*b[i][k];)是常数时间的,所以整个算法的时间复杂度是O(n^3)。这是矩阵乘法的一个常见时间复杂度,特别是在没有使用任何优化技术(如Strassen算法或并行计算)的情况下。所以,这个代码段的时间渐进复杂度是
O(n^3)。

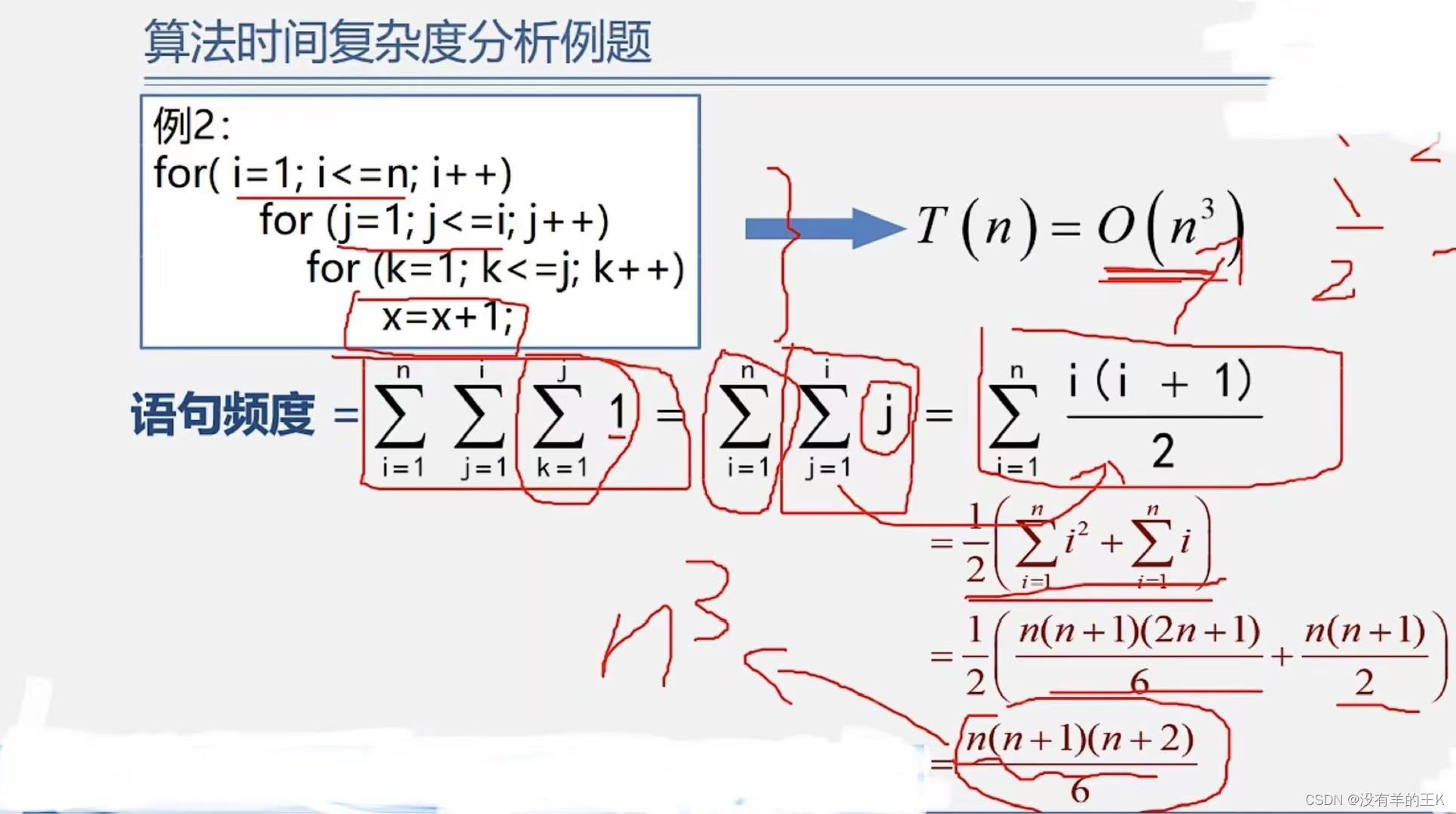

一般情况下:时间复杂度可以直接找循环嵌套最深的
算法时间复杂度的渐进表示法:
我们仅仅需要比较数量级(数量级越大越不好)
算法的渐进时间复杂度是对算法的时间效率的度量,即分析一个算法执行所需要的时间。它表示随问题规模n的增大,算法执行时间的增长率和某个函数f(n)的增长率相同。换句话说,当问题规模n趋于无穷大时,算法运行时间的增长趋势的度量即为渐进时间复杂度。
为了分析一个算法的时间复杂度,通常需要考察算法中基本语句的执行次数,找出其与问题规模n的函数关系f(n)。基本语句是执行次数与算法的执行次数成正比的语句,它是算法中的关键操作。然后,用O(f(n))来表示算法的复杂度。这里,O表示大O表示法,用于描述算法执行时间的上界。