目录

简介

快速排序的实现步骤

快排的时间复杂度

快排的空间复杂度

霍尔法

证明 key >= x 

left从key的位置出发的原因

霍尔法代码 (递归)

挖坑法

流程及其展开图

代码 (递归)

前后指针法 

 前后指针法的步骤及其动图

代码(递归) 

 快排的优化

一、三数取中

二、随机数取中

三、三路划分 

---

简介

快速排序由C. A. R. Hoare在1962年提出，快速排序是一种高效的排序算法，其核心思想是通过一次排序将待排序的数据分割成独立的两部分，其中一部分的所有数据都比另一部分的数据要小，然后再按此方法对这两部分数据分别进行快速排序，以实现整个序列有序。下文将给出实现快排的三种方法：霍尔法、挖坑法、前后指针法。同时也会给出面对一些特殊场景做出的优化。

快速排序的实现步骤

> 从待排序序列中选一个元素作为基准（key）。

> 重新排序数组，将小于基准值元素放在基准值左边，将大于基准值元素放在基准值右边。

> 对左、右两边分别进行快速排序。

快排的时间复杂度

快速排序的时间复杂度取决于基准元素的选择方式。如果每次都选择最小或最大的元素作为基准，快速排序的最坏情况时间复杂度将达到 O(n^2)。快速排序的最佳情况和平均情况下的时间复杂度都为 O(nlogn)。

快排的空间复杂度

如果原数组每次都均匀的分为两个子数组，那么递归的最大深度为logn,空间复杂度就为O(logn),但如果每次排序时数组中的所有元素都大于基准值，或者都小于基准值，也就是偏向一端，则为最坏情况，递归的最大深度为n,所以空间复杂度为O(n).

综上，快排的空间复杂度为O(logn)~O(n)

霍尔法

一趟快速排序的动图：

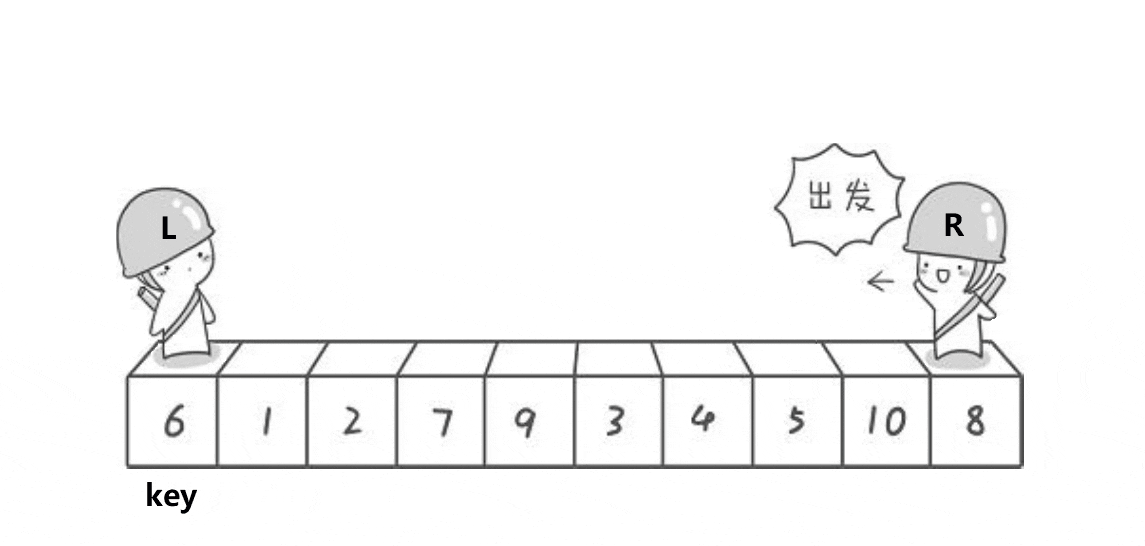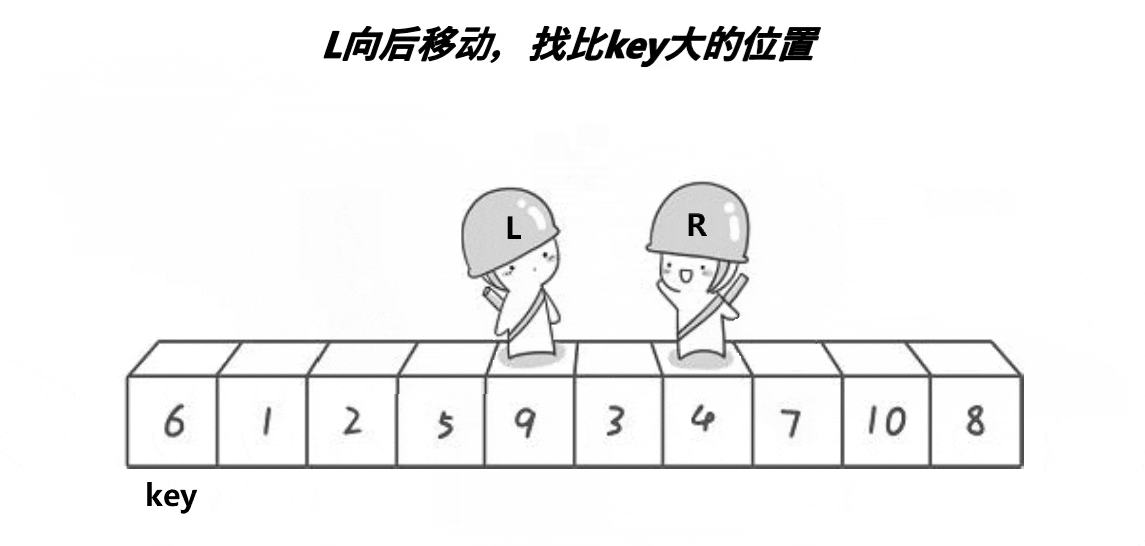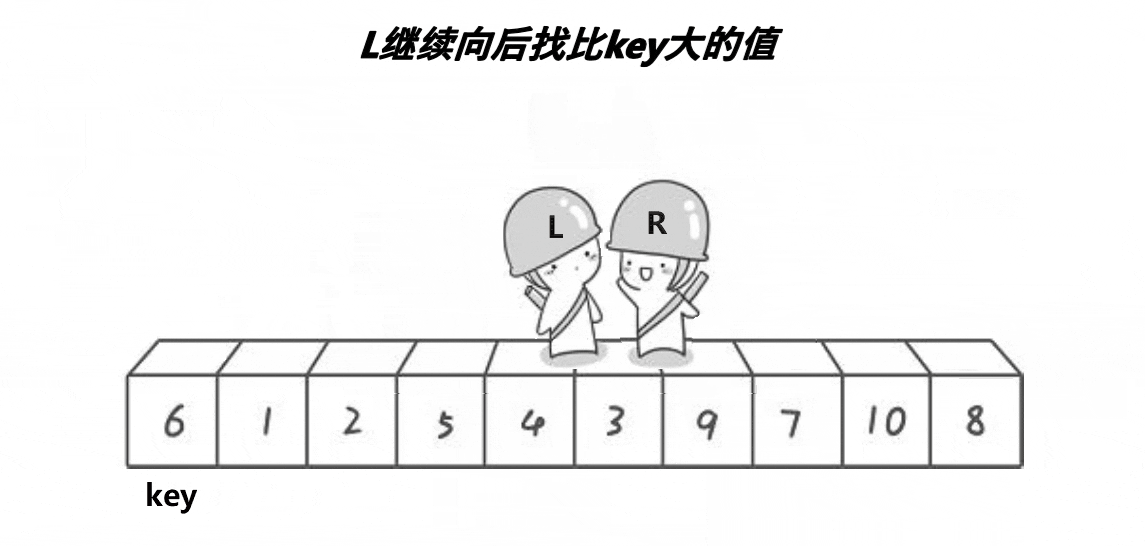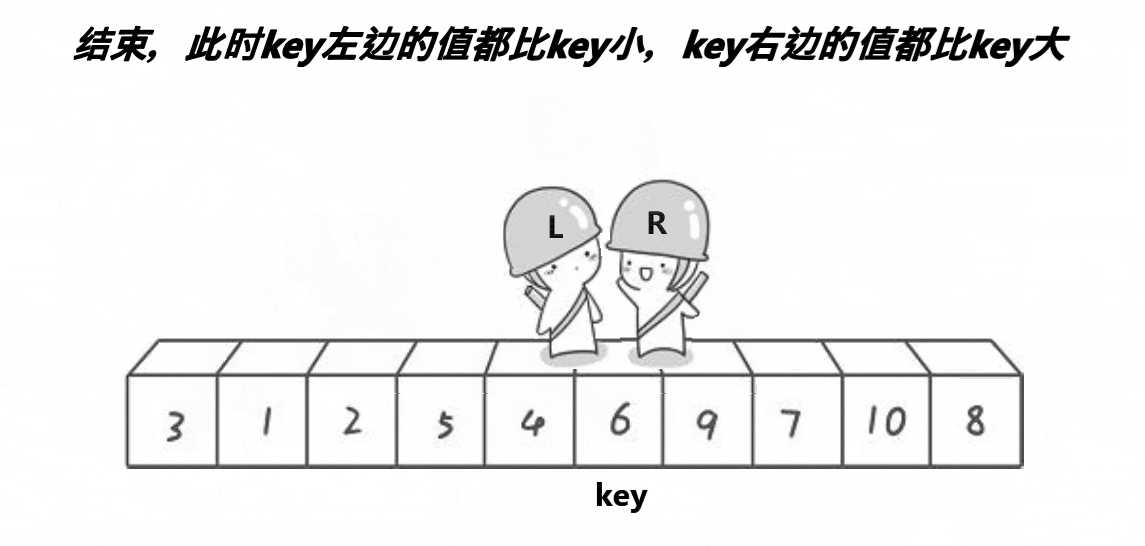
一趟快速排序的步骤

第一步：选基准值key，一般选择首元素作为基准值，这里key = 6

第二步：定义两个指针left和right，当然，这里的指针只是个形象的说法，其实是控制下标，left从首元素开始往右遍历，也就是说，left从key的位置开始遍历，而不是key的下一个位置，这里的原因下面再谈，right从最后一个元素的位置开始往左遍历，right先出发找小于key的值，找到之后停下，接着left出发，找大于key的值，找到之后停下，交换left和right位置的值，重复这一过程，直到left和right相遇

第三步：left和right相遇后，将相遇位置的值(记作x)与keyi(key对应的下标)位置的值交换，结果是，相遇位置的值为基准值key，keyi位置的值为x，到这里，也许会有疑问：x <= key 一定成立吗？答案是肯定的，下面会给出证明。

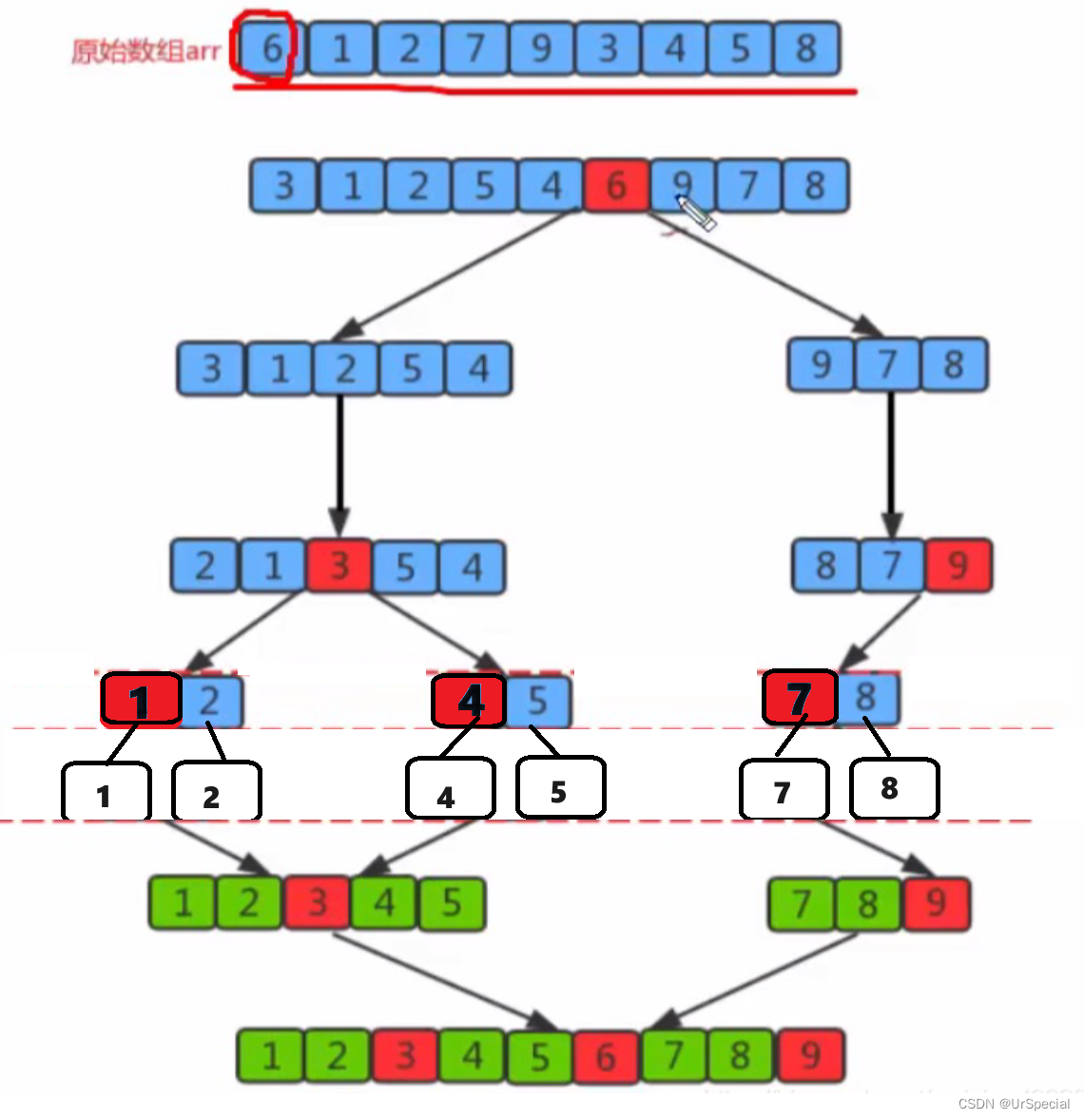
 一趟快速排序展开图：

 完成一趟快速排序后，继续对数组进行分割，以上图为例，继续将数组分为[0,keyi - 1] 和 [keyi + 1, 9]两个子数组，重复上面的操作，再继续将数组分割，重复上面的操作……直到数组只有一个元素时停止分割。

证明 key >= x 

> 左边做key，右边先走，保证了相遇位置的值比key小 or 相遇位置为key的位置

> 右边做key,左边先走，保证了相遇位置的值比key小 or 相遇位置为key的位置

以左边做key为例：

相遇时，有两种情况：要么left不动，right在找小的过程中遇到left,要么right不动，left在找大的过程中遇到right。

left遇到right：也就是right是不动的，right不动意味着找到了比key小的值，所以left遇上right时，相遇位置的值是小于key的。

right遇到left: right 遇到left有两种情况。一，数组是逆序的，right没有找到小于key的值，直接就与left相遇了， 此时，相遇位置的值为key；二，因为是right先走，right走一次后没有直接与left相遇就说明right找到了比key小的值了，此时left开始走，找大，因为是right遇到left,这里隐含了left是不动的，left不动，意味着找到了比key大的值，随后开始交换，交换后left位置的值比key小，所以right在遇到left时，相遇位置的值是小于key的。

综上，左边做key，右边先走这一情况，相遇位置的值一定小于或等于key。

left从key的位置出发的原因

交换结束后，错误是显而易见的，所以left应从keyi的位置出发。

霍尔法代码 (递归)

#include <stdio.h>void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void QuickSort(int* a, int begin, int end)
{//将数组分解到只有一个元素if (begin >= end) return;int keyi = begin;//这里取key的下标，方便交换数据int left = begin, right = end;while (left < right){//右边找小， 左边找大while (left < right && a[right] >= a[keyi]) right--;while (left < right && a[left] <= a[keyi]) left++;Swap(&a[left], &a[right]);}//将相遇位置的值交换到keyiSwap(&a[left], &a[keyi]);keyi = left;//更新keyi//数组此时被分为三个部分 [begin,keyi - 1] [keyi] [keyi + 1, end]//对[begin,keyi - 1]和[keyi + 1, end]进行快速排序QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{int a[] = { 5,1,4,2,7,6,0,2,8,1,9 };int n = sizeof(a) / sizeof(int);Print(a, n);QuickSort(a, 0, n - 1);Print(a, n);return 0;
}

挖坑法

流程及其展开图

挖坑法的步骤 

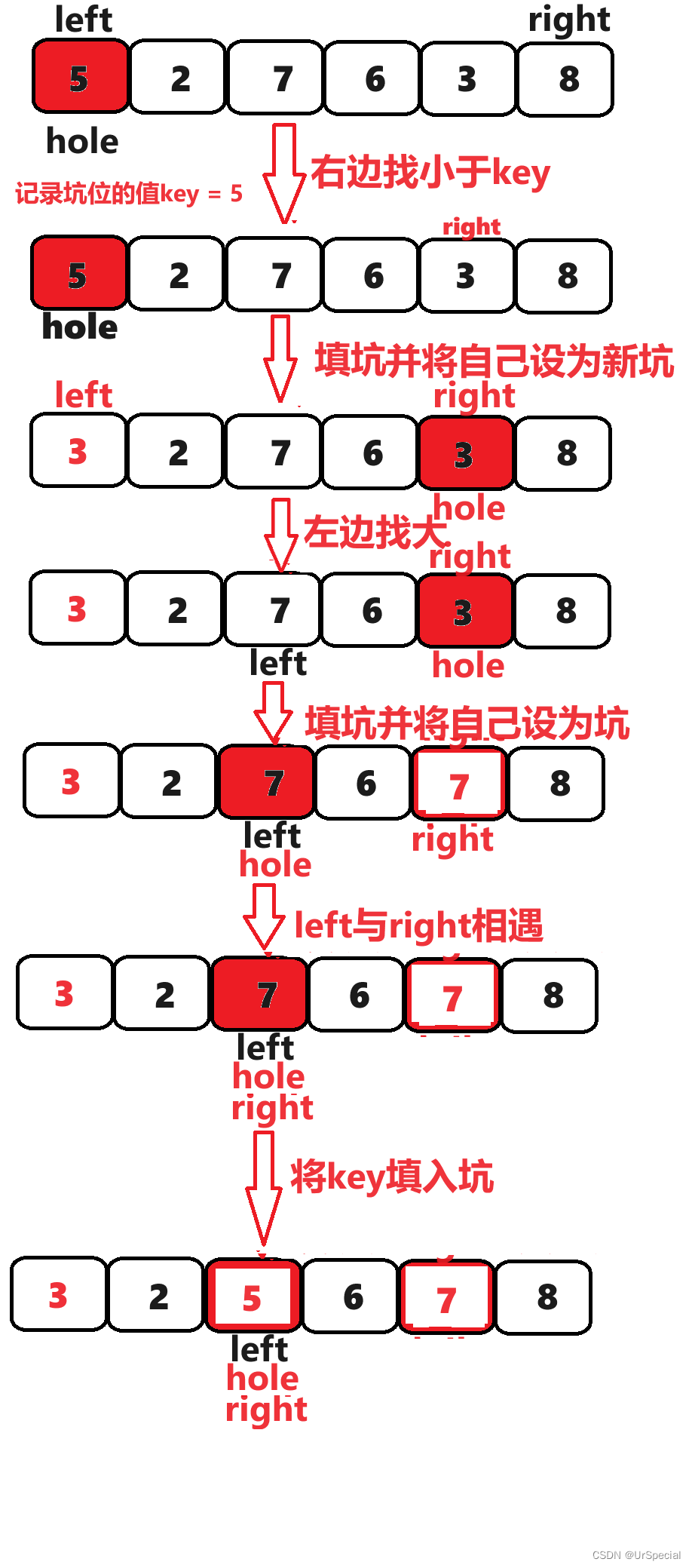
一、取首元素为基准值，将首元素的值保存在key中,并将首元素的位置设为坑hole

二、right从右往左找小于key的值填坑，填坑后将自己设为坑

三、left从从左往右找大于key的值填坑，填坑后将自己设为坑

……

重复以上操作，直到left和right相遇，因为left和right之间总有一个要为坑，所以相遇位置一定为坑，接着，将key的值填入相遇位置，即填入坑中。

代码 (递归)

#include <stdio.h>void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int key = a[begin];int hole = begin;int left = begin, right = end;while (left < right){//右边找小于key的值填坑while (left < right && a[right] >= key) right--;a[hole] = a[right];hole = right;//填坑后将自己设为坑//左边找大于key的值填坑while (left < right && a[left] <= key) left++;a[hole] = a[left];hole = left;//填坑后将自己设为坑}a[hole] = key;//将key给相遇位置//再处理剩下的区间QuickSort(a, begin, hole - 1);QuickSort(a, hole + 1, end);
}int main()
{int a[] = { 4,1,7,3,9,0,1,5,7,8 };int n = sizeof(a) / sizeof(int);Print(a, n);QuickSort(a, 0, n - 1);Print(a, n);return 0;
}

前后指针法 

 前后指针法的步骤及其动图

前后指针法的步骤

一、确定基准值key

二、cur找小于key的值，如果找到了，就++prev，再交换prev位置和cur位置的值

三、当cur出了数组边界后，交换prev位置的key位置的值

仔细观察，会发现，当遇到比key大的值后，prev和cur将拉开，它们之间的值都大于key，所以上面的第二步是先++prev再交换。

代码(递归) 

void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int keyi = begin;int prev = begin, cur = begin + 1;/*while (cur <= end){if (a[cur] < a[keyi]){++prev;Swap(&a[prev], &a[cur]);}cur++;}*///while循环也可以这样写,避免将同一位置的值进行交换while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{int a[] = { 4,1,7,3,9,0,1,5,7,8 };int n = sizeof(a) / sizeof(int);Print(a, n);QuickSort(a, 0, n - 1);Print(a, n);return 0;
}

 快排的优化

一、三数取中

以上三种方法中，都是以最左边为基准值key，如果每次选key都恰好选中中位数或接近中位数，效率就很好（如果二叉树有一定基础，就会明白，这里就不深入讲了），时间复杂度为O(n * logn)。如果待排数组为逆序或者接近逆序，那么时间时间复杂度为O(N^2)。通常，快速排序被认为是，在所有同数量级O(nlogn)的排序方法中，其平均性能最好。但是，如果待排序列有序或基本有序时，快速排序将蜕化为冒泡排序，其时间复杂度为O(n^2),采用三数取中可大大改善快排在最坏情况下的性能。

从左中右三数中选出中间值作为基准值key。代码如下：

int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] < a[left]){if (a[right] < a[mid])return mid;else if (a[right] > a[left]) return left;else return right;}else{if (a[mid] < a[right]) return mid;else if (a[right] < a[left]) return left;else return right;}
}

 对上述前后指针法的代码进行优化，代码如下：

int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] < a[left]){if (a[right] < a[mid])return mid;else if (a[right] > a[left]) return left;else return right;}else{if (a[mid] < a[right]) return mid;else if (a[right] < a[left]) return left;else return right;}
}void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int mid = GetMidIndex(a, begin, end);Swap(&a[mid], &a[begin]);//交换到起始位置，不用改下面的代码int keyi = begin;int prev = begin, cur = begin + 1;/*while (cur <= end){if (a[cur] < a[keyi]){++prev;Swap(&a[prev], &a[cur]);}cur++;}*///while循环也可以这样写,避免将同一位置的值进行交换while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

对其他方法的优化同理，将中间值交换到起始位置就无需改代码。

二、随机数取中

int mid = left + (rand() % (right - left));

代码：

#include <stdio.h>
#include <time.h>void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void QuickSort(int* a, int left, int right)
{if (left >= right) return;int mid = left + (rand() % (right - left));Swap(&a[mid], &a[left]);int keyi = left;int end = right;while (left < right){while (left < right && a[right] >= a[keyi]) right--;while (left < right && a[left] <= a[keyi]) left++;Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;QuickSort(a, 0, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{srand(NULL);int a[] = { 4,1,6,3,7,4,3,9,0,8 };int n = sizeof(a) / sizeof(int);Print(a, n);QuickSort(a, 0, n - 1);Print(a, n);return 0;
}

三、三路划分 

快速排序的三路划分是为了解决数组中存在大量重复元素时，快速排序算法性能下降的问题。在传统的快速排序算法中，选择一个基准元素，将数组划分为两个子数组，其中一个子数组中的元素都小于基准元素，另一个子数组中的元素都大于等于基准元素，然后对两个子数组进行递归排序。

然而，当数组中存在大量重复元素时，传统的快速排序算法会导致不必要的比较和交换操作，从而降低算法的效率。三路划分的主要目的是将数组划分为三个部分，分别存放小于、等于和大于基准元素的值，以减少不必要的比较和交换操作。

通过三路划分，可以将相等的元素集中在一起，减少了对相等元素的重复比较和交换操作，在面对大量重复元素的场景时，提高了算法的效率。相对于双路快排来说，三路划分的适应性更强。 

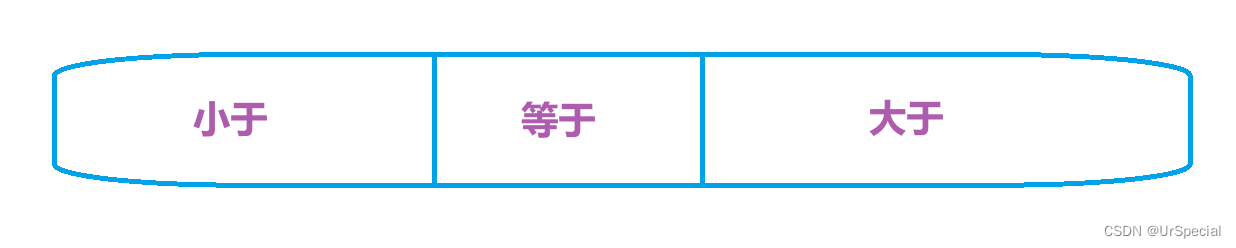
三路划分方法 

一、如果a[cur] < key,则交换cur和left位置的值，然后left++,cur++

二、如果a[cur] > key,则交换cur和right位置的值，然后right--

三、如果a[cur] == key,则cur++

三路划分展开图：

可以看到，等于key的值都集中在了中间，后面，我们只需处理区间[begin,left-1]和区间[right + 1,end]即可，这样，就减少了对相等元素的比较和交换。

代码：

#include <stdio.h>int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[mid] < a[left]){if (a[mid] > a[right]) return mid;else if (a[right] > a[left]) return left;else return right;}else{if (a[left] > a[right]) return left;else if (a[right] > a[mid]) return mid;else return right;}
}void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void QuickSort(int* a, int begin, int end){if (begin >= end) return;int mid = GetMidIndex(a, begin, end);int left = begin, cur = begin + 1, right = end;Swap(&a[mid], &a[left]);int key = a[left];while (cur <= right){if (a[cur] < key){Swap(&a[cur], &a[left]);left++;cur++;}else if (a[cur] > key){Swap(&a[cur], &a[right]);right--;}else{cur++;}}QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}int main()
{int a[] = { 5,3,9,0,1,7,3,8,4,2,0,1,7,2 };int n = sizeof(a) / sizeof(int);Print(a, n);QuickSort(a, 0, n - 1);Print(a, n);return 0;
}