面试经典150题【71-80】

112.路径总和

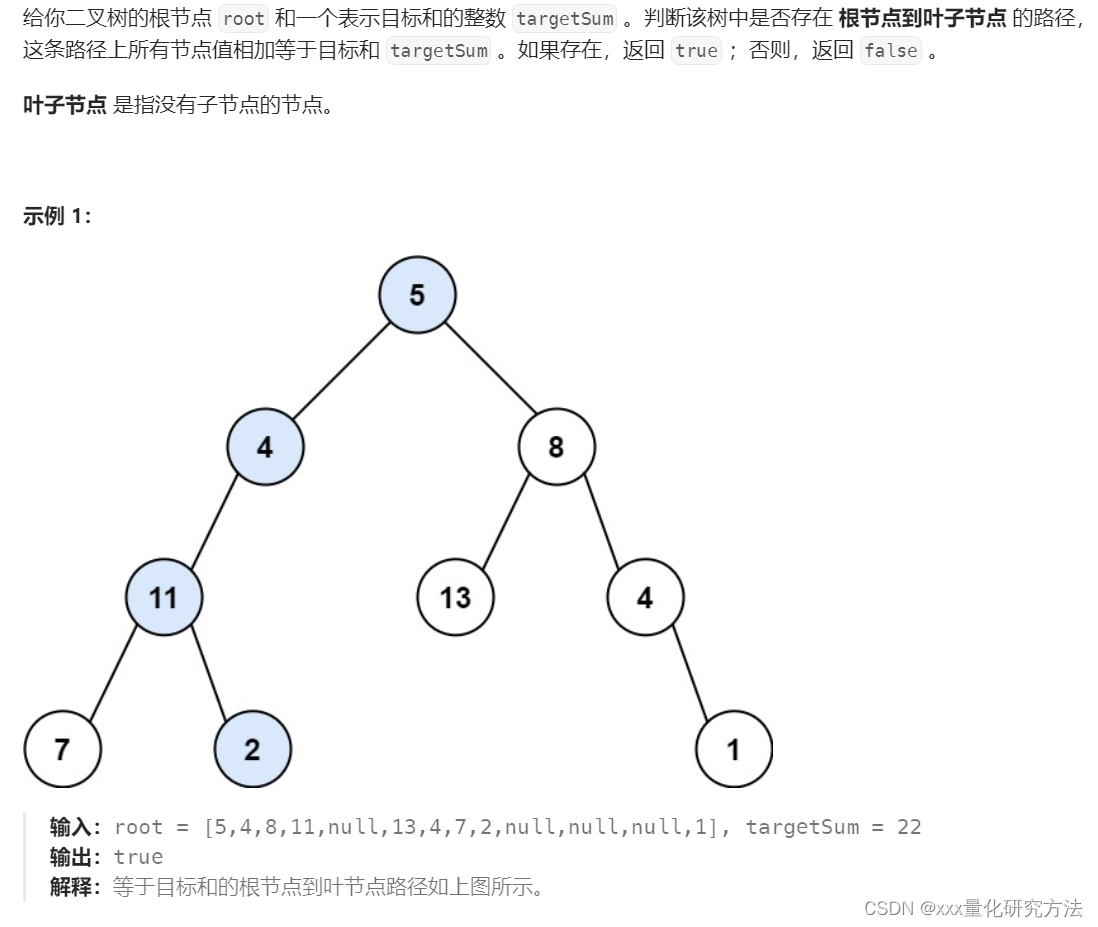
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null) return false;//叶子节点if(root.left ==null && root.right==null){return root.val == targetSum;}//看左子节点和右子节点，并且要减去当前值return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val);}
}

129.求根节点到叶子节点的数字之和

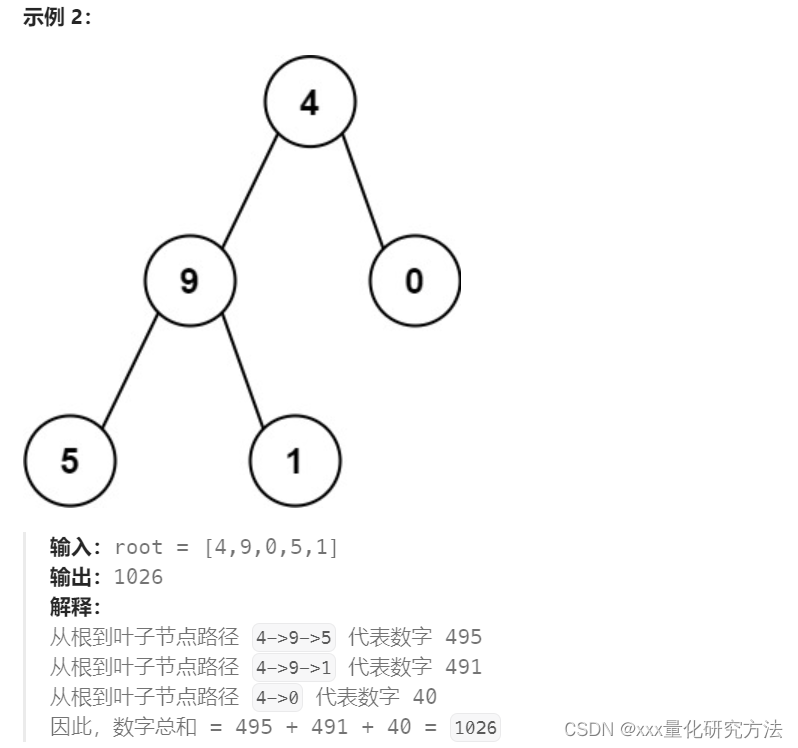
这种DFS的，还是要搞一个辅助函数

class Solution {public int sumNumbers(TreeNode root) {return helper(root,0);}public int helper(TreeNode root,int ans){if(root==null) return 0;int temp=ans*10+root.val;if(root.left==null && root.right==null){return temp;}return helper(root.left,temp)+helper(root.right,temp);}
}

124.二叉树中的最大路径和（要思考）

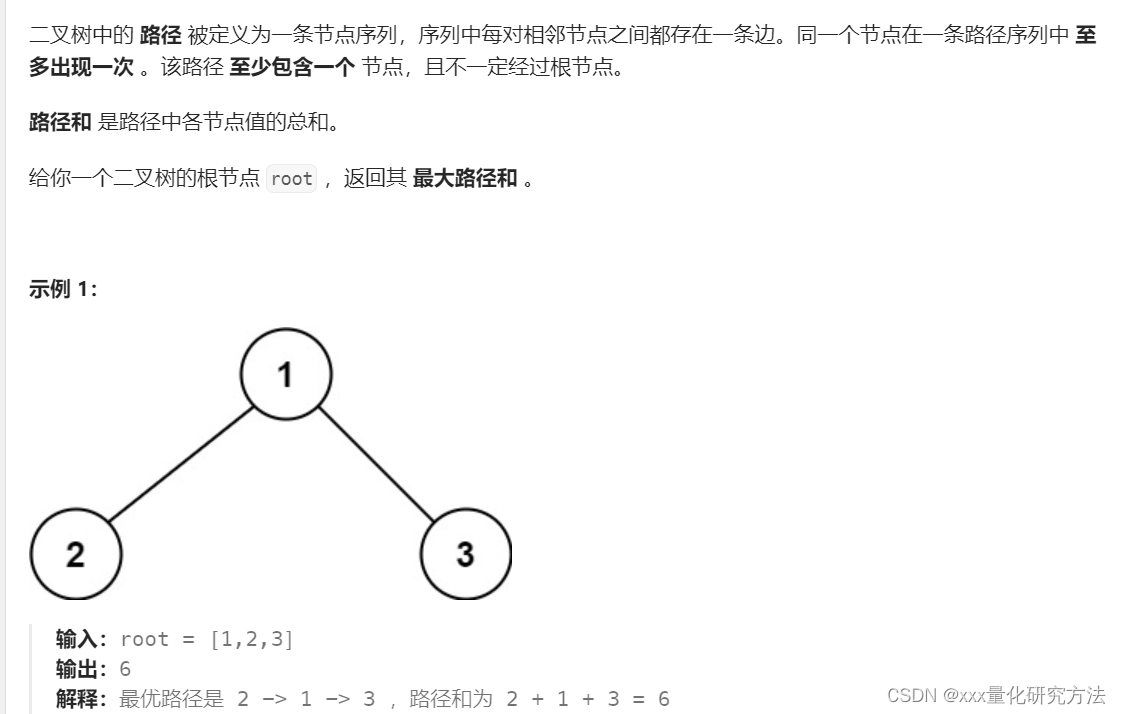
这个题要好好思考一下。
首先要明白，maxGain求的是什么，求的是经过我这个root节点以后，单边的最大值。因为只有这样，才能搞 root.val +maxGain(root.left) +maxGain(root.right)的值为最大。

class Solution {int maxSum = Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {maxGain(root);return maxSum;}public int maxGain(TreeNode node) {if (node == null) {return 0;}// 递归计算左右子节点的最大贡献值// 只有在最大贡献值大于 0 时，才会选取对应子节点int leftGain = Math.max(maxGain(node.left), 0);int rightGain = Math.max(maxGain(node.right), 0);// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值int priceNewpath = node.val + leftGain + rightGain;// 更新答案maxSum = Math.max(maxSum, priceNewpath);// 返回节点的最大贡献值return node.val + Math.max(leftGain,rightGain);}
}

173.二叉树迭代搜索器

中序遍历树，存到数组里即可。

222.完全二叉树节点的个数

BFS遍历一遍求节点就行。DFS直接递归也可以。
不过因为是完全二叉树，则可以判断是否完全，若是完全则直接2的n次方-1，否则就DFS，
ans = 1 + func(root.left) + func(root.right)

236.二叉树的最近公共祖先

要不p,q在root的两侧，要不p和q其中一个是root一个是小弟。
终止条件：

if(root == null || root == p || root == q) return root;

如果为叶子节点，自然什么都没找到。如果找到一个节点，就返回一个节点。
比如 root == p == 3 ,则直接返回3.
遍历其左右子树

TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);

如果左右子树都有值，则答案为root
如果只有一个有值，则为其中的一边。答案返回的就是最近公共祖先

if(left == null) return right;
if(right == null) return left;
return root;

199.二叉树的右视图

简单的BFS即可，当 i == size -1 的时候加入答案数组中。

637.二叉树的层平均值

BFS

102.二叉树的层序遍历

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {if(root==null) return new ArrayList<>();List<List<Integer>> res=new ArrayList<>();Queue<TreeNode> queue=new LinkedList<TreeNode>();queue.add(root);while(!queue.isEmpty()){int size=queue.size();List<Integer>list=new ArrayList<Integer>();for(int i=0;i<size;i++){TreeNode node=queue.poll();list.add(node.val);if(node.left!=null) queue.add(node.left);if(node.right!=null) queue.add(node.right);}res.add(list);}return res;}
}

103.二叉树的锯齿形层序遍历

设置一个boolean变量，每回合进行翻转。