Introduction to Multi-Armed Bandits——05 Thompson Sampling[3]

参考资料

1. Russo D J, Van Roy B, Kazerouni A, et al. A tutorial on thompson sampling[J]. Foundations and Trends® in Machine Learning, 2018, 11(1): 1-96.

2. ts_tutorial

项目代码地址: https://github.com/yijunquan-afk/bandit-learning.git

到目前为止，我们所考虑的 Bernoulli bandit 和最短路径例子中的共轭性质有利于简单和计算效率高的贝叶斯推理。 计算效率制定模型时的一个重要考虑。 然而，很多情况下我们需要更复杂的模型，而精确的贝叶斯推理在计算上是难以实现的。 幸运的是，我们有一些准确的方法可以用来对后验分布进行近似采样。（Approximations）

在本节中，我们将讨论四种近似后验取样的方法。Gibbs sampling、Langevin Monte Carlo、从Laplace approximation中抽样和bootstrap。 作为一个例子，我们考虑在线最短路径问题的一个变体。

一、Binary Feedback

在之前最短路的基础上。假设图代表了 $M$ 阶的 binomial bridge，让每个 ${\theta }_e$ 独立分布，且是 gamma分布的，$\mathbb{E}[{\theta }_e]=1$, $\mathbb{E}[{\theta }_e^2]=1.5$，观察值根据如下公式产生：
$$\begin{array}{c}{y}_t|\theta \sim \{\begin{array}{ll}1& \text{with probability }\frac{1}{1+\exp \left({\sum }_{e\in x_t}{\theta }_e-M\right)}\\ 0& \text{otherwise.}\end{array}\end{array}$$

我们将奖励看作评级，$r_t=y_t$。例如，一个Internet路线推荐服务。每天，系统推荐一条路线 $x_t$ ，并收到司机的反馈 $y_t$ ，表示该路线是否可取。当实现的遍历时间 ${\sum }_{e\in x_t}$ 低于先前的期望值 $M$ ，反馈往往是积极的(1)，反之亦然(0)。

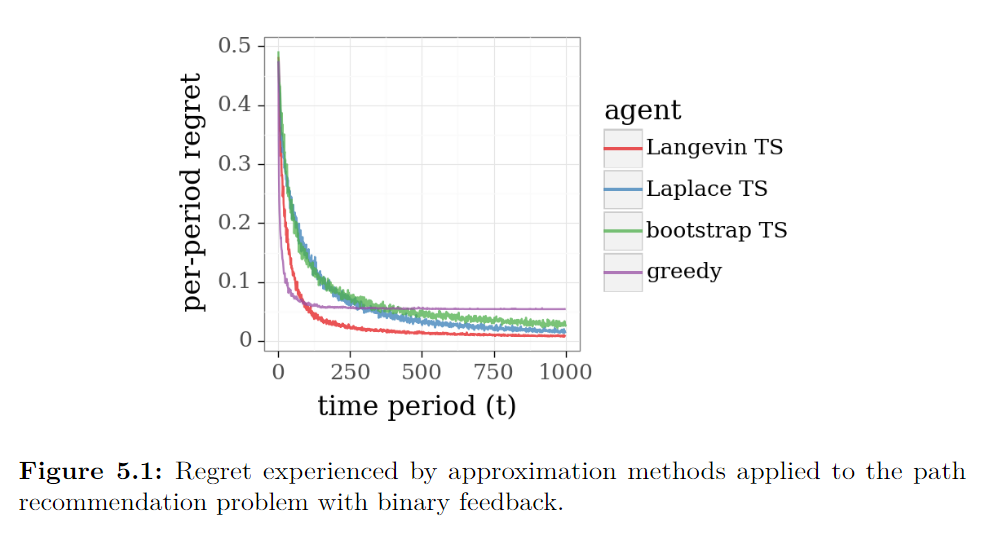
这个新的模型不具有在第四节中利用的共轭性质，也不适合于有效的精确贝叶斯推理。 不过，这个问题可以通过近似的方法来解决。 为了说明这一点，下图显示了三个近似版本的TS应用于twenty-stage binomial bridge 的在线最短路问题的结果。这些算法利用了Langevin Monte Carlo、Laplace近似和bootstrap这三种方法。 作为比较的基线，还绘制了贪心算法的应用结果。

在本节中，我们让 $f_{t-1}$ 代表在历史为 ${\mathbb{H}}_{t-1}=((x_1,y_1),\dots ,(x_{t-1},y_{t-1}))$ 的条件下 $\theta$ 的后验密度。TS算法通过从 $f_{t-1}$ 中抽取参数向量 $\hat{\theta }$ 并求解 $\hat{\theta }$ 下的最优路径来生成动作 $x_t$ 。我们所描述的方法产生了一个样本 $\hat{\theta }$ ，其分布近似于后验 ${\hat{f}}_{t-1}$，当精确的后验抽样不可行时，可以近似地实现TS的功能。

二、Gibbs Sampling

可以阅读这篇文章：机器学习中的MC、MCMC、Gibbs采样

Gibbs抽样是一种通用马尔可夫链蒙特卡罗(MCMC)算法，用于从多元概率分布中提取近似样本。它产生了一个采样参数序列 $({\hat{\theta }}^n:n=0,1,2,\dots )$，形成了一个稳定分布的马尔可夫链 $f_{t-1}$ 。在合理的技术条件下，该马尔可夫链的极限分布为其平稳分布，${\hat{\theta }}^n$ 的分布收敛于 $f_{t-1}$。

Gibbs抽样从最初的猜测 ${\hat{\theta }}^0$ 开始，迭代遍历$n=1,\dots ,N$，对于第n次扫描，该算法迭代分量 $k=1,\dots ,K$，对于每个 $k$ 生成一维边际分布:

$$f_{t-1}^{n,k}({\theta }_k)\propto f_{t-1}(({\hat{\theta }}_1^n,\dots ,{\hat{\theta }}_{k-1}^n,{\theta }_k,{\hat{\theta }}_{k+1}^{n-1},\dots ,{\hat{\theta }}_K^{n-1}))$$

按照 ${\hat{\theta }}_k^n\sim f_{t-1}^{n,k}$ 对第k个分量进行采样。经过 $N$ 次的扫描，向量 ${\hat{\theta }}^N$ 被认为是近似的后验样本。

Gibbs抽样适用于广泛的问题，即使在从 $f_{t-1}$ 抽样时，在计算上也往往是可行的。这是因为从一维分布中取样比较简单。 也就是说，对于复杂的问题，Gibbs抽样在计算上仍有一定要求。 例如我们的二元反馈的路径推荐问题。在这种情况下，很容易实现Gibbs抽样的一个版本，它可以在一分钟内产生一个接近于后验样本的结果。然而， 在数百个时间段内运行数千次模拟是相当耗时的，需要更有效的近似方法。

三、Laplace Approximation

可以参考贝叶斯推断之拉普拉斯近似、拉普拉斯近似法。

我们现在讨论一种方法，用高斯分布来逼近潜在的复杂后验分布。然后，来自这个较简单的高斯分布的样本可以作为感兴趣的后验分布的近似样本。 Chapelle和Li 提出了这种方法，用广告点击率的逻辑回归模型来近似显示广告问题中的TS。

设 $g$ 表示 ${\mathbb{R}}^K$ 上的概率密度函数，我们希望从中抽样。如果 $g$ 是单峰的（unimodal），它的对数密度 $\ln (g(\varphi ))$ 在其模 $\overline{\varphi }$ 上是严格凹的，$g(\varphi )=e^{\ln (g(\varphi ))}$在 $\overline{\varphi }$ 周围急剧地达到顶峰。考虑围绕其模进行全局近似是很自然的。对数密度的二阶泰勒近似给出如下：

$$\ln (g(\varphi ))\approx \ln (g(\overline{\varphi }))-\frac{1}{2}(\varphi -\overline{\varphi }{)}^{\top }C(\varphi -\overline{\varphi }),$$

其中$$C=-{\nabla }^2\ln (g(\overline{\varphi })).$$

我们可以使用

$$\tilde{g}(\varphi )\propto e^{-\frac{1}{2}(\varphi -\overline{\varphi }{)}^{\top }C(\varphi -\overline{\varphi })}.$$

作为 $g$ 的近似值。这与具有均值 $\overline{\varphi }$ 和协方差 $C^{-1}$ 的高斯分布密度成正比，因此

$$\tilde{g}(\varphi )=\sqrt{|C/2\pi |}{e}^{-\frac{1}{2}(\varphi -\overline{\varphi }{)}^{\top }C(\varphi -\overline{\varphi })}.$$

我们称之为 $g$ 的 Laplace Approximation. 由于有高效的算法来生成高斯分布的样本，这为从 $g$ 中近似取样提供了一种可行的方法。

作为一个例子，让我们考虑拉普拉斯近似在例子binary feedback中的应用。贝叶斯规则表明 $f_{t-1}$ 的后验密度 $\theta$ 满足:

$$f_{t-1}(\theta )\propto f_0(\theta )\prod _{\tau =1}^{t-1}{\left(\frac{1}{1+\exp \left({\sum }_{e\in x_{\tau }}{\theta }_e-M\right)}\right)}^{y_{\tau }}{\left(\frac{\exp \left({\sum }_{e\in x_{\tau }}{\theta }_e-M\right)}{1+\exp \left({\sum }_{e\in x_{\tau }}{\theta }_e-M\right)}\right)}^{1-y_{\tau }}$$

众数（mode） $\overline{\theta }$ 可以通过最大化 $f_{t-1}$ 来有效计算，$f_{t-1}$ 是对数凹的。然后从高斯分布中抽取一个近似的后验样本 $\hat{\theta }$，其平均值为 $\overline{\theta }$，协方差矩阵为 $(-{\nabla }^2\ln (f_{t-1}(\overline{\theta })){)}^{-1}$

拉普拉斯近似法非常适合于binray feedback，因为对数后验密度是严格内凹的，其梯度和Hessian矩阵可以有效计算。

我们采用了牛顿方法和回溯线搜索法，使 $\ln (f_{t-1)}$ 达到最大。 遗憾会衰减，最终应该消失。在我们的例子中，拉普拉斯近似法的表现不如Langevin Monte Carlo。这可能是由于后验分布不够接近高斯。而在TS的实际应用中，拉普拉斯近似是一种流行的方法。

四、Langevin Monte Carlo

我们现在描述一种替代性的马尔科夫链蒙特卡罗（MCMC）方法，它使用目标分布的梯度信息。 让 $g(\varphi )$ 表示在 ${\mathbb{R}}^K$ 上的一个对数凹的概率密度函数，我们希望从中取样。假设 $\ln (g(\varphi ))$ 是可微的，其梯度是可有效计算的。 Langevin dynamics 首先出现在物理学中，指的是扩散过程
$$d{\varphi }_t=\nabla \ln (g({\varphi }_t))dt+\sqrt{2}d{B}_t\text{\hspace{1em}(5.1)}$$
其中 $B_t$ 是一个标准布朗运动过程，这个过程有 $g$ 作为其唯一的静止分布，在合理的技术条件下， ${\varphi }_t$ $的分布会迅速收敛到这个静止分布。因此，模拟（5.1）提供了一种从 $g$ 中近似取样的方法。

通常情况下，我们可以用欧拉离散化来代替这个随机微分方程：
$${\varphi }_{n+1}={\varphi }_n+ϵ\nabla \ln (g({\varphi }_n))+\sqrt{2ϵ}{W}_{n}n\in \mathbb{N}\text{\hspace{1em}(5.2)}$$
其中 $W_1,W_2,\dots$ 是独立同分布的标准高斯随机变量， $ϵ>0$ 是一个小的步长。与梯度上升法一样，在这种方法下，${\varphi }_n$ 倾向于向密度 $g({\varphi }_n)$ 增加的方向漂移。然而，每一步都会注入随机的高斯噪声 $W_n$ ，因此，对于大的 $n$ ，${\varphi }_n$ 的位置是随机的。

我们对这个方法做了两个标准的修改以提高计算效率。

• 首先，根据最近的工作，我们实现了$stochasticgradient$。Langevin Monte Carlo，它使用采样的小批数据来计算近似梯度而不是精确梯度。我们的实现使用了100个mini-batch的规模。当观测值少于100个时，我们遵循Markov链(5.2)，进行精确梯度计算。当收集到超过100个观测值时，我们遵循(5.2)，但在每一步使用基于100个数据点的随机子样本的估计梯度 $\nabla \ln ({\hat{g}}_n({\varphi }_n))$ 。

• 我们的第二个修改涉及到使用一个预处理矩阵来提高马尔科夫链(5.2)的混合率。对于binary feedback中的路径推荐问题，我们发现对数后验密度在后期变得病态的。由于这个原因，梯度上升法收敛到后验众数（mode）的速度非常慢。有效的优化方法应该利用二阶信息。同样，由于条件较差，我们可能需要选择一个极小的步长 $ϵ$ ，导致(5.2)中的Markov链混合缓慢。Langevin MCMC可以通过模拟马尔科夫链，用对称正定预处理矩阵 $A$ 实现

$${\varphi }_{n+1}={\varphi }_n+ϵA\nabla \ln (g({\varphi }_n))+\sqrt{2ϵ}{A}^{1/2}{W}_{n}n\in \mathbb{N}$$

其中 $A^{1/2}$ 表示 $A$ 的矩阵平方根。我们采取 ${\varphi }_0={\text{argmax}}_{\varphi }\ln (g(\varphi ))$，所以链的初始化是在后验众数（mode）。并采取预处理矩阵 $A=-({\nabla }^2\ln (g(\varphi )){|}_{\varphi ={\varphi }_0}{)}^{-1}$ 为该点的负逆Hessian。

五、Bootstrapping

bootstrap的解释可以看这个：用 Bootstrap 进行参数估计大有可为

作为一种替代方法，我们讨论了一种基于 statistical bootstrap 的方法，它甚至可以容纳非常复杂的密度。 我们介绍一个适用于我们在本教程中涉及的例子。

与拉普拉斯近似法一样，我们的bootstrap法也假定$\theta$ 是从欧几里得空间 $R^K$中抽取。首先考虑一个标准的bootstrap法，用于评估 $\theta$ 的最大似然估计的抽样分布。该方法产生了一个假设的历史 $\widehat{{\mathbb{H}}_{t-1}}=(({\hat{x}}_1,{\hat{y}}_1),\dots ,({\hat{x}}_{t-1},{\hat{y}}_{t-1}))$ ，它由 $t-1$ $action-observation$ 对组成，每个人都从 ${\mathbb{H}}_{t-1}$ 均匀采样并替换。然后，我们在假设的历史下最大化 $\theta$ 的可能性，对于我们的最短路径推荐问题来说，这个可能性是这样的:
$${\hat{L}}_{t-1}(\theta )=\prod _{\tau =1}^{t-1}{\left(\frac{1}{1+\exp \left({\sum }_{e\in {\hat{x}}_{\tau }}{\theta }_e-M\right)}\right)}^{{\hat{y}}_{\tau }}{\left(\frac{\exp \left({\sum }_{e\in {\hat{x}}_{\tau }}{\theta }_e-M\right)}{1+\exp \left({\sum }_{e\in {\hat{x}}_{\tau }}{\theta }_e-M\right)}\right)}^{1-{\hat{y}}_{\tau }}$$
最大化器中的随机性 ${\hat{L}}_{t-1}$ 反映了最大似然估计的抽样分布的随机性。不幸的是，这种方法并没有考虑到代理人的先验。一个更严重的问题是，它严重低估了智能体在初始时期的真实不确定性。我们将以一种简单的方式克服这些缺点。

该方法的步骤如下。首先，像以前一样，我们抽取一个假设的历史 $\widehat{{\mathbb{H}}_{t-1}}=(({\hat{x}}_1,{\hat{y}}_1),\dots ,({\hat{x}}_{t-1},{\hat{y}}_{t-1}))$，它由$t-1$ $action-observation$ 对组成，每个人都从 ${\mathbb{H}}_{t-1}$ 均匀采样并替换。接下来，我们从先验分布 $f_0$ 中抽取一个样本 ${\theta }^0$。让 $\Sigma$ 表示先验 $f_0$ 的协方差矩阵。最后，我们解决最大化问题
$$\hat{\theta }={\text{argmax}}_{\theta \in {\mathbb{R}}^k}{e}^{-(\theta -{\theta }^0{)}^{\top }\Sigma (\theta -{\theta }^0)}{\hat{L}}_{t-1}(\theta )$$
并将 $\hat{\theta }$ 视为近似的后验样本。这可以看作是对后验密度的随机近似 ${\hat{f}}_{t-1}$ 的最大化，其中 ${\hat{f}}_{t-1}(\theta )\propto e^{-(\theta -{\theta }^0{)}^{\top }\Sigma (\theta -{\theta }^0)}{\hat{L}}_{t-1}(\theta )$ 是指如果先验是均值为 ${\theta }^0$、协方差矩阵为 $\Sigma$ 的高斯分布，而观察的历史是 ${\hat{\mathbb{H}}}_{t-1}$，后验密度会是什么。当收集到的数据很少时，样本中的随机性大多源于先验样本 ${\theta }_0$ 的随机性。这种随机的先验样本鼓励智能体在早期阶段进行探索。当 $t$ 很大时，已经收集了大量的数据，可能性通常压倒了先验样本，样本中的随机性主要来自于对历史 ${\hat{\mathbb{H}}}_{t-1}$ 的随机选择。

在最短路径推荐问题中，${\hat{f}}_{t-1}(\theta )$ 是对数凹的，因此可以有效地实现最大化。 同样，为了得出图中报告的计算结果，我们采用了牛顿方法和回溯线搜索来最大化 $\ln ({\hat{f}}_{t-1})$。

从图中可以看出，对于我们的例子，bootstrap法的表现与拉普拉斯近似法差不多。 bootstrap法的一个优点是它是非参数性的，无论后验分布的函数形式如何，它都可以合理地工作，而拉普拉斯近似法则依赖于高斯近似法，Langevin Monte Carlo 法则依赖于log-concavity和其他规则性假设。

六、健全性检查

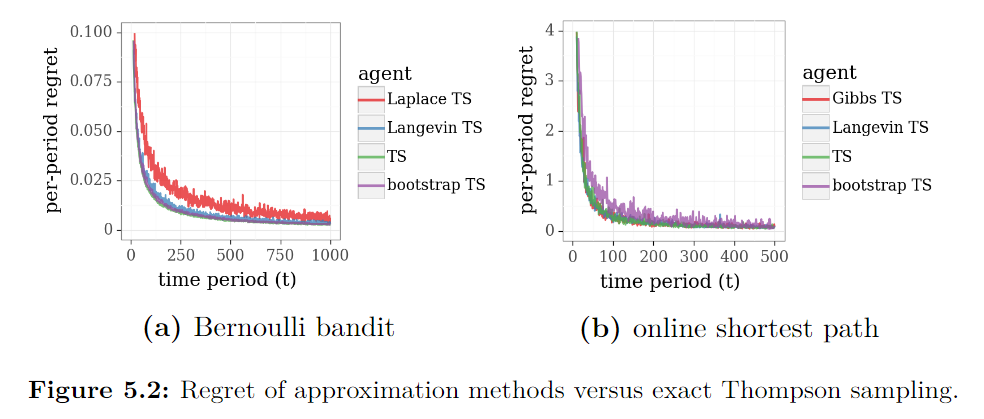
图5.1展示了Laplace approximation、Langevin Monte Carlo和bootstrap方法在应用于路径推荐问题时，从二项反馈中学习，以随着时间的推移提高性能。然而，这可能会让人疑惑，确切的TS是否会提供更好的性能。由于我们没有可处理的方法来执行该问题的精确TS，因此在本节中，我们将我们的近似方法应用于精确TS可处理的问题。这使得可以比较精确方法和近似方法的性能。

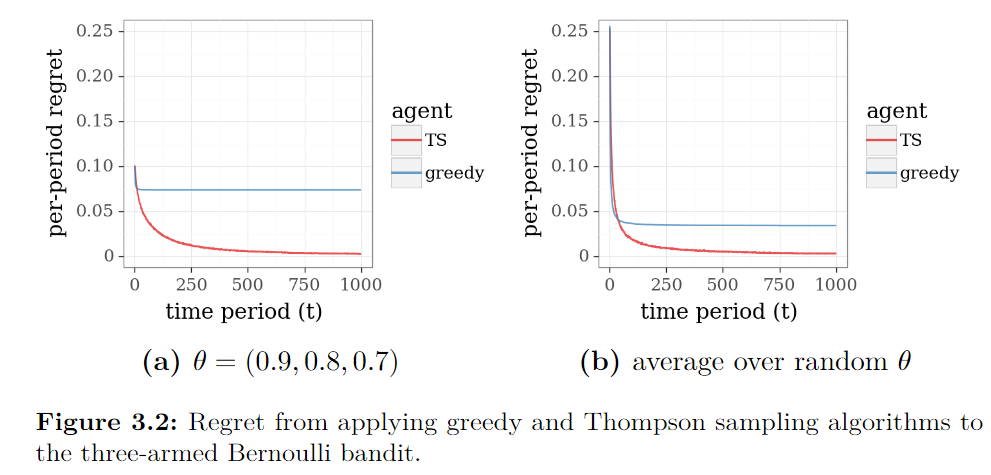
回顾一下三臂beta-Bernoulli强盗问题，其贪心算法和TS算法的结果如上图所示。对于这个问题，$\theta$ 的各分量在后验分布下是独立的。因此，Gibbs抽样可以得到精确的后验样本。 因此，使用Gibbs抽样的近似版本的性能将与精确的TS完全相同。下图中的a绘制了应用Laplace approximation、Langevin Monte Carlo和bootstrap方法的结果。对于这个问题，我们的近似方法提供的性能与精确的TS在质量上相似，拉普拉斯近似法的表现比其他方法略差。

接下来，考虑具有correlated边延迟的在线最短路径问题。如图b所示。应用拉普拉斯近似方法与适当的变量替换达到了与精确TS相同的结果。 图中将这些结果与Gibbs sampling、Langevin Monte Carlo和bootstrap方法所产生的结果进行了比较。同样，近似方法产生了有竞争力的结果，bootstrap的效果略逊于其他方法。