一算法简介

详细介绍

两种基本方法

二算法实践

1）实数三分

拓展：秦九韶算法计算多项式

方法1：直接模拟累加

方法二：根据秦九韶算法

1）模板三分法

题目描述

解法

2）三分求极值

题目描述

分析

3）Line belt

题目描述

分析

2）整数三分

算法模板

三题目练习

函数

题目描述

题目分析

题目解答

附录

一算法简介

详细介绍

三分法求单峰（或单谷）的极值是二分法的简单扩展

单峰函数和单谷函数如下图所示，函数fx再区间【L,R】内只有一个极值v，再极值点两边函数是单调变化的。以单峰函数为例，在v的左边是严格单调递增的，在右边是严格单调递减的。

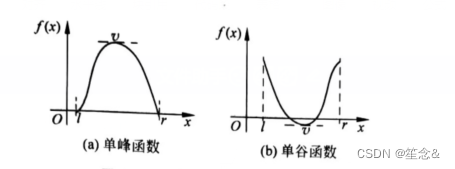
下面的讲解都以求单峰极值为例：
如何求单峰函数最大值的近似值？虽然不能直接用二分法，但是只要稍微变形一下就可以了

在【L，R】内任取两个点：mid1和mid2，把函数分为3段，有以下情况：

1）若f(mid1)<f(mid2),极值点v一定在 mid1 的右侧

mid1和 mid2 要么都在v的左侧,要么分别在v的两侧,如图所示。下一步,令L=mid1,区间从[L,r]缩小为[mid1,r],然后再继续把它分成3段.

2）若f(mid1)>f(mid2),极值点一定在 mid2 的左侧,如图所示

下一步,令r=mid2,区间从[l,r ]缩小为[l,mid2]

不断缩小区间,就能使区间[l,r]不断逼近 ,从而得到近似值

如何取 mid1和 mid2?

两种基本方法

(1)三等分: mid1 和 mid2 为[l,r]的三等分点,那么区间每次可以缩小 1/3

(2)近似三等分:计算[l,r]中间点 mid=(+r)/2,然后让 mid1 和 mid2 非常接近mid,如mid1=mid-eps,mid2=mid+eps,其中 eps 是一个很小的值,那么区间每次可以缩小接近一半。

近似三等分比三等分要稍微快一点。不过,在有些情况下,eps 过小可能导致这两种方法算出的结果相等,导致判断错方向,所以不建议这么写。从复杂度上看,0(log;n)和 O(logn)是差不多的

注意：

单峰函数的左右两边要严格单调,否则可能在一边有 f(mid1)-=f(mid2),导致无法判断如何缩小区间

二算法实践

1）实数三分

拓展：秦九韶算法计算多项式

方法1：直接模拟累加

题目条件：n为最高的次数，a数组为系数，x为给定的值。

double f(int n,double a[],double x)
{int i;double p=a[0];for(i=1;i<=n;i++)p+=(a[i]*pow(x,i));return p;
}

方法二：根据秦九韶算法

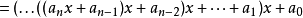
在这里插入图片描述

可转化为：
在这里插入图片描述
故我们可以从内往外递推的计算多项式的值。

double f(int n,double a[],double x)
{int i;double p=a[n];//从最内层开始for(i=n;i>0;i--)p=a[i-1]+p*x;return p;
}

两种算法时间复杂度分析：
第一种由于的时间复杂度大致为O(N)=n²。若将pow函数改为快速幂函数，则可优化为O(N)=n(logn);
第二种的时间复杂度为O(N)=n；

1）模板三分法

题目描述

如题，给出一个 N 次函数，保证在范围 [l, r] 内存在一点 x，使得 [l, x] 上单调增，[x, r] 上单调减。试求出 x 的值。

输入格式

第一行一次包含一个正整数 N 和两个实数 l, r，含义如题目描述所示。

第二行包含 N + 1 个实数，从高到低依次表示该 N 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 x 的值。若你的答案与标准答案的相对或绝对误差不超过 10^{-5} 则算正确。

样例

输入

3 -0.9981 0.5
1 -3 -3 1

输出

-0.41421

解法

三等分法：mid1和mid2为[l,r]的三等分点

# include <stdio.h>
const double eps = 1e-6;
int n;
double a[15];
double f(double x){//计算函数值int i;double s = 0;for(i=n;i>=0;i--)	s = s*x + a[i]; //注意函数求值的写法return s;
}int main(){double L,R;int i;scanf("%d %lf %lf",&n,&L,&R);for(i=n;i>=0;i--)scanf("%lf",&a[i]);while(R-L>eps) // for(int i = 0;i<100;it+){ //用for循环也可以double k =(R-L)/3.0;double mid1 =L+k,mid2 = R-k;if(f(mid1) > f(mid2)) R = mid2;else L = mid1;}printf("%.5f\n",L);return 0;
}

近似三等分法：mid1和mid2在[l,r]的中间点附近

# include <stdio.h>
const double eps = 1e-6;
int n;
double a[15];
double f(double x){//计算函数值int i;double s = 0;for(i=n;i>=0;i--)	s = s*x + a[i]; //注意函数求值的写法return s;
}int main(){double L,R;int i;scanf("%d %lf %lf",&n,&L,&R);for(i=n;i>=0;i--)scanf("%lf",&a[i]);while(R-L>eps) // for(int i = 0;i<100;it+){ //用for循环也可以double mid=L+(R-L)/2;if(f(mid-eps) > f(mid)) R = mid;else L = mid;}printf("%.5lf\n",L);return 0;
}

2）三分求极值

题目描述

在直角坐标系中有一条抛物线 y-azz+bx+c 和一个点 P(x，y),求点P 到抛物线的最短距离d。
输入:第1行输入5个整数:a,b,c,工;y。a,b,c 构成抛物线的参数,工,y 表示P点
坐标。-200<a,b,c,工,y<200。
输出: 一个实数 d,保留3位小数(四舍五入)。

分析

直接求距离很麻烦，观察本题的距离d，发现满足单谷函数的特征，用三分法即可

3）Line belt

题目描述

给定两条线段 AB、CD,一个人在 AB 上跑时速度为 P,在 CD 上跑时速度为Q,在其他地方跑时速度为 R。求从A 点跑到D 点最短的时间。

输入:第1行输入测试数量 T。对于每个测试输入3行:第1行为4 个整数,表示A点和B点的坐标,即 Ax,Ay,Bx,By; 第2行为4 个整数,表示 C点和D点的坐标,即Cx,Cy,Dx,Dy;第3行为3个整数 P、Q、R。

数据范围:0<Ax,Ay,Bx,By,Cx,Cy,Dx,Dy≤1000,1≤P,Q,R<10

输出:从A 点到D点的最短时间,四舍五入取两位小数。

分析

从A 点出发,先走到线段 AB 上一点 X,然后走到线段 CD上一点Y,后到 D 点,时间为
time=l AX I / P+IXYI/R+IYDI/Q

假设已经确定了X,那么目标就是在线段 CD 上找一点Y,使|XYI/R+IYDI/Q小，这是一个单峰函数。三分套三分就可以了,这是计算几何中的常见题型。

2）整数三分

算法模板

while(right-left >2){     //2或其他数int mid1=left+(right - left)/3;    //三等分，1/3处int mid2=right-(right - left)/3;    //三等分，2/3处if(check(mid1)> check(mid2))...    //移动rightelse...    //移动left
}

注意：第一行的right-left>2，如果写成right>left，当right-left<3时会陷入死循环

三题目练习

函数

题目描述

给定n 个二次函数f(a),(a),..., fn(a) (均形如 aa’ + ba + c)，设F() =max(fi(a),f2(a),..., n(c)，求F(a)在区间 0,1000] 上的最小值
输入格式
输入第一行为正整数工，表示有工组数据
每组数据第一行一个正整数n，接着n 行，每行3个整数 a,b,c，用来表示每个二次函数的3个系数，注意二次函数有可能退化成一次。
输出格式
每组数据输出一行，表示 F()的在区间 0,1000] 上的最小值。答案精确到小数点后四位，四舍五入。

样例：

输入

输出

0.0000
0.5000

题目分析

主要考了一点关于函数的知识罢，题目大意是给你一堆二次函数，F(x)定义为对于每一个x取每一个函数对应的y的最大值，题目是求F[x]在一定区间中的最小值。

因为同时考虑100个函数有些过于困难，我决定先从简单的两个函数开始

我们可以看到，这里函数的最小值很容易找见，同时我们关注到整个函数是一个下凸函数我们知道，开口向上的二次函数是下凸函数，那么假使两人下凸函数取最大值还是下凸函数，就说明题目给的F(X)是一个下凸函数，我们就可以用三分法来寻找最值。
换而言之，本题的难点在于
已知f(x),g(a)为下凸函数，证明h(a) = ma((a),g(a))是一个下凸函数
证明如下
对于任意的0 < a < 1
总有f(ax1 +(1 - a)2) < af(a1) + (1 - a)f(a2) < ah(a1) + (1 - a)h(2)
同理，对于g(a)也有相似的结论
那么很容易推出
h(ax1 + (1 - a)a2) = max(f(ax1 + (1 - a)2),g(ax1 + (1 - a)a2)) < ah(al) + (1 -a)h(x2)
这就证明了h(x)是一个凸函数
那么我们只需要在上面跑个三分求最值就ok了。

题目解答

#include<stdio.h>
#include<math.h>
int T;
int n;
int a[100010],b[100010],c[100010];
//已知f(x),g(x)为下凸函数，
//则h(x)=max(f(x),g(x))是一个下凸函数。
//h(x)=max(f(x),g(x)...)
double f(double x)					//计算某一点的h(x) 
{double ans=0;int i;for(i=1;i<=n;i++)ans=fmax(ans,a[i]*1.0*x*x+b[i]*1.0*x+c[i]);return ans;
}
int main()
{scanf("%d",&T);while(T--){int i;scanf("%d",&n);for(i=1;i<=n;i++)scanf("%d %d %d",&a[i],&b[i],&c[i]);double l=0,r=1000;while(fabs(r-l)>1e-9)				//三分 {double mid=l+(r-l)/2;if(f(mid-1e-9)>f(mid))	l=mid;else		r=mid;}printf("%.4lf\n",f(l));}
}