问题出现的场景：

输入：

import torch
import torch.nn as nn
a=torch.randint(10,[3,4])
# a=torch.DoubleTensor(a)
# a=a.double()
print(a)
layer_norm=nn.LayerNorm(4)
layer_norm(a)

我就是想测试一下经过layernorm之后的输出会变成什么样

但是报错了

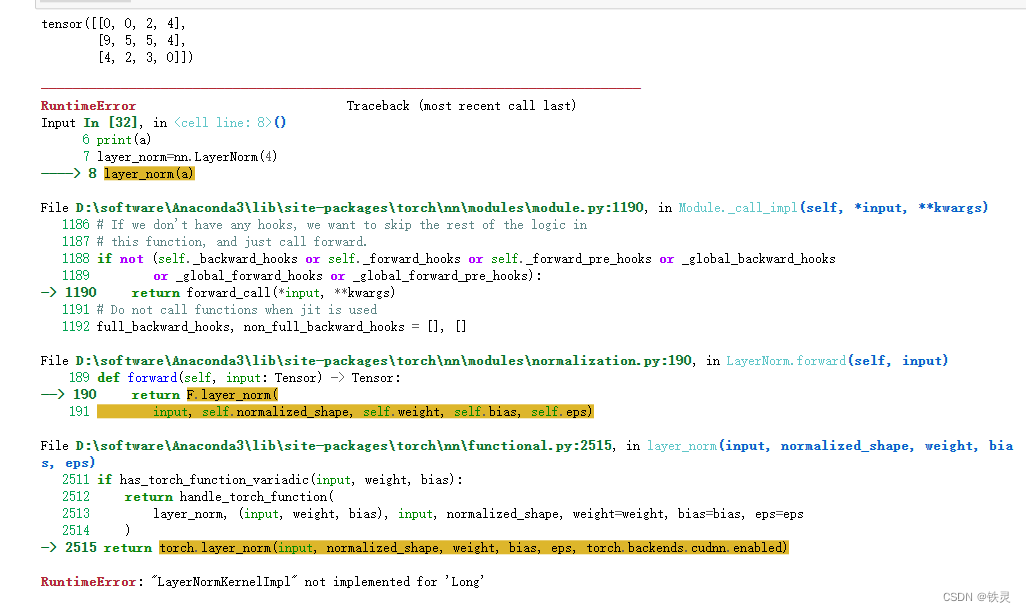
 意思是正则化不能处理类型为long(长整型)的数据

然后我想到在网络中梯度下降也不能处理整形数据

哪解决方案就出来了，讲其转换成浮点型

我用dtype=float来指定数据类型

输入：

import torch
import torch.nn as nn
a=torch.randint(10,[3,4],dtype=float)print(a)
layer_norm=nn.LayerNorm(4)
layer_norm(a)

又出错了

 问题是，期待的是double数据类型，但是找到的是float数据类型

首先要知道是没有办法通过dtypy指定double数据类型的

但是可以通过a.double（）来指定，但是依然会出现上面的错误，为什么呢？

已经按照他报错的问题进行修改了，还是不行，查阅资料：

 从上面上面来看float64应该是符合我们要求的double数据类型，从上面的输出来看，指定dtype=float时已经讲数据转换成float64了，但还是报错了

我们尝试用.to(torch.float32)将其转换成单精度浮点数，没想到成功了

输入：

import torch
import torch.nn as nn
a=torch.randint(10,[3,4]).to(torch.float32)
print(a)
layer_norm=nn.LayerNorm(4)
layer_norm(a)

 输出：

 总结：nn.LayerNorm期待的输入是float32的，，，但jupyter notebook这个报错的确挺让人迷惑的。