引言

上一节介绍了从深度学习的角度介绍了推断，并介绍了推断的目的和困难。本节将继续介绍推断的核心思想。

回顾：推断的目的与困难

推断的目的

推断不仅局限于深度生成模型。实际上，所有基于概率图结构的模型，特别是基于隐变量的概率图模型，都需要推断任务。推断的目的主要包含两种情况：

• 推断自身就是推断的目的。也就是说，推断本身就是处理相关任务的一个结果。例如以隐马尔可夫模型为核心的动态模型($\text{Dynamic Model}$)。
  基于齐次马尔可夫假设与观测独立性假设下的动态模型，其模型内部的随机变量结点存在严格限制：
  
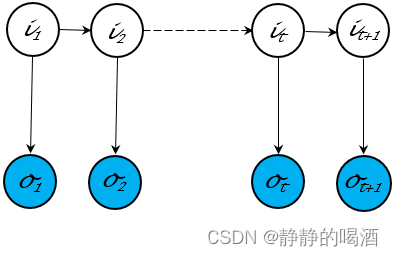
  在这种确定结构下的推断任务多种多样。如解码任务($\text{Decoding}$)——维特比算法($\text{Viterbi}$)，求值问题——前向算法($\text{Forward Algorithm}$)等等，这些任务本身就是推断任务的目标。
• 模型学习任务中需要推断。例如$\text{EM}$算法($\text{Expectation Maximization,EM}$)在参数迭代的过程中，要对隐变量的后验概率$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$进行计算/近似计算：
  下面公式中分别描述'狭义EM算法'与‘广义EM算法’中E步的表示。
  $$\{\begin{array}{l}\log \mathcal{P}(\mathcal{X};\theta )=\text{ELBO}\iff \mathcal{Q}(\mathcal{Z})=\mathcal{P}(\mathcal{Z}\mid \mathcal{X})\\ \\ {\hat{\mathcal{Q}}}^{(t+1)}(\mathcal{Z})=\underset{\mathcal{Q}(\mathcal{Z})}{\mathrm{argmax}}\text{ELBO}\iff \mathcal{Q}(\mathcal{Z})\approx \mathcal{P}(\mathcal{Z}\mid \mathcal{X})\end{array}$$

并不是一上来就可以针对陌生的变量进行推断，必须要在模型给定，并且当前模型参数已知的情况下，才能够执行推断。

• 这个说法和‘模型学习任务中需要推断’并不冲突。除非是结构简单的模型，否则很难通过一次步骤直接得到参数的精确解。因此，通常是基于随机初始化的模型参数，通过若干次迭代得到参数最优解的近似解。
• 例如广义EM算法的坐标上升法($\text{Coordinate Ascent}$),再比如‘随机梯度变分推断’($\text{Stochastic Gradient Variational Inference,SGVI}$)中的梯度上升法($\text{Gradient Ascent,GA}$)等等。

推断的困难

推断困难的原因主要有两个：

• 随机变量的概率能够表示，但计算代价太大。依然以隐马尔可夫模型中的解码问题为例，它的目标可表示为如下形式：
  $$\hat{\mathcal{I}}=\underset{\mathcal{I}}{\mathrm{argmax}}\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )$$
  其中$\mathcal{I}$表示基于时间/序列的随机变量集合：I={i1,i2,⋯,iT}\mathcal I = \{i_1,i_2,\cdots,i_T\}I={i1​,i2​,⋯,iT​}，假设每一个随机变量$i_t(t=1,2,\cdots ,T)$均属于离散型随机变量：
  it=qk(qk∈Q={q1,q2,⋯,qK})i_t = q_k(q_k\in \mathcal Q = \{q_1,q_2,\cdots,q_{\mathcal K}\})it​=qk​(qk​∈Q={q1​,q2​,⋯,qK​})
  那么随机变量集合$\mathcal{I}$可以得到 ${\mathcal{K}}^T$种不重复的状态序列组合。而最终目标仅需要一个最优组合：
  I^={i^1,i^2,⋯,i^T}\hat {\mathcal I} = \{\hat {i}_1,\hat i_2,\cdots,\hat i_{T}\}I^={i^1​,i^2​,⋯,i^T​}
  如果将所有序列组合全部求解出来去比较，这个计算代价极大。因而可采用维特比算法这种基于贪心策略的方法进行求解。

• 由于随机变量之间关系过于复杂，导致随机变量的概率根本无法表示。玻尔兹曼机($\text{Boltzmann Machine}$)就是一个典型的例子。玻尔兹曼机中观测变量、隐变量内部可能存在关联关系，这种结构导致后验概率$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$没有办法精准地梳理开。
  当然，$\text{Hinton}$老爷子也给出了一种基于$\text{MCMC}$的求解方式。

  假设观测变量集合$\mathcal{V}$与隐变量集合$\mathcal{H}$ 分别表示如下：
  {H={h1,h2,⋯,hm}V={v1,v2,⋯,vn}\begin{cases} \mathcal H = \{h_1,h_2,\cdots,h_m\} \\ \mathcal V = \{v_1,v_2,\cdots,v_n\} \end{cases}{H={h1​,h2​,⋯,hm​}V={v1​,v2​,⋯,vn​}​
  那么某一隐变量hj(j∈{1,2,⋯,m})h_j(j \in \{1,2,\cdots,m\})hj​(j∈{1,2,⋯,m})的后验概率分布可表示为：
  推导过程详见玻尔兹曼机——$\text{MCMC}$求解后验概率，就是因为$h_j$和$h_{-j}$存在关联关系，才导致$\mathcal{P}(h_j\mid \mathcal{V})\approx \mathcal{P}(h_j\mid \mathcal{V},h_{-j})$的近似操作。
  $$\begin{array}{rl}\mathcal{P}(h_j\mid \mathcal{V},h_{-j})& =\frac{\mathcal{P}(h_j,\mathcal{V},h_{-j})}{\mathcal{P}(h_{-j},\mathcal{V})}\\ & =\frac{\mathcal{P}(\mathcal{H},\mathcal{V})}{{\sum }_{h_j}\mathcal{P}(\mathcal{H},\mathcal{V})}{h}_{-j}=(h_1,\cdots ,h_{j-1},h_{j+1},\cdots ,h_m)\end{array}$$

推断的核心思想——优化

推断的推导过程在$\text{EM}$算法、变分推断过程中已经详细地介绍过。其底层逻辑就是：将隐变量的后验概率求解问题 转化成优化问题，即基于极大似然估计，将观测变量(样本)的对数似然函数($\text{log-likelihood}$) $\log \mathcal{P}(\mathcal{V})$转化成证据下界$\text{ELBO}$ + $\text{KL}$散度，并最大化$\text{ELBO}$的问题：

• 已知样本集合$\mathcal{V}$包含$N$个样本，并包含$n$个随机变量：
  V={v(i)}i=1Nv(i)=(v1(i),v2(i),⋯,vn(i))T\mathcal V = \{v^{(i)}\}_{i=1}^N \quad v^{(i)} = (v_1^{(i)},v_2^{(i)},\cdots,v_n^{(i)})^TV={v(i)}i=1N​v(i)=(v1(i)​,v2(i)​,⋯,vn(i)​)T

• 关于观测变量集合$\mathcal{V}$的对数似然函数$\log \mathcal{P}(\mathcal{V})$可表示为如下形式：

  • 样本之间‘独立同分布’。
  • 在配分函数——对数似然梯度中提到，可以在最前面乘以一个常数项$\frac{1}{N}$,即$\frac{1}{N}{\sum }_{i=1}^N\log \mathcal{P}(v^{(i)})$。
该常数项本身恒正，在极大似然估计求解过程中并不会产生影响。但从蒙特卡洛方法($\text{Monte Carlo Method}$)逆向推导的思路中可以观察到，它明显是一个期望：$\frac{1}{N}{\sum }_{i=1}^N\log \mathcal{P}(v^{(i)})\approx {\mathbb{E}}_{v^{(i)}\sim {\mathcal{P}}_{data}}\left[\log \mathcal{P}(v^{(i)})\right]$,其中${\mathcal{P}}_{data}$表示真实样本分布。
    $$\begin{array}{rl}\log \mathcal{P}(\mathcal{V})& =\log \left[\prod _{i=1}^N\mathcal{P}(v^{(i)})\right]\\ & =\sum _{i=1}^N\log \mathcal{P}(v^{(i)})\end{array}$$

• 继续观察关于某个样本$v^{(i)}$的对数似然函数$\log \mathcal{P}(v^{(i)})$是如何分解的。

  基于贝叶斯定理，引入观测变量$v^{(i)}$对应模型的隐变量$h^{(i)}$，可将$\log \mathcal{P}(v^{(i)})$表示成如下形式：
  $$\log \mathcal{P}(v^{(i)})=\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]$$
  引入一个人为设定的分布$\mathcal{Q}(h^{(i)}\mid v^{(i)})$，并将其转化为如下形式：

  • 需要注意的是，这个分布$\mathcal{Q}(h^{(i)}\mid v^{(i)})$是一个以$v^{(i)}$为条件的后验概率分布。
  • 将$\log \mathcal{P}(v^{(i)})$使用$\mathcal{I}$进行替代。
    $$\begin{array}{rl}\mathcal{I}& =\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\cdot \frac{\mathcal{Q}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]\\ & =\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]+\log \left[\frac{\mathcal{Q}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]\end{array}$$

  观察第一项$\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]$和$\log \mathcal{P}(v^{(i)})=\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]$之间，可以将其理解成：人为设定分布$\mathcal{Q}(h^{(i)}\mid v^{(i)})$替代了$\mathcal{P}(h^{(i)}\mid v^{(i)})$分布的位置；而$\log \left[\frac{\mathcal{Q}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]$可理解为：分布$\mathcal{Q}(h^{(i)}\mid v^{(i)})$与分布$\mathcal{P}(h^{(i)}\mid v^{(i)})$之间存在的某种关联关系。

  分别对等式两端基于$\mathcal{Q}(h^{(i)}\mid v^{(i)})$求解积分：
  其中$\mathcal{I}$中不包含$h^{(i)}$,因而有${\int }_{h^{(i)}}\mathcal{I}\cdot \mathcal{Q}(h^{(i)}\mid v^{(i)})d{h}^{(i)}=\mathcal{I}{\int }_{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})d{h}^{(i)}=\mathcal{I}\cdot 1=\mathcal{I}$(概率密度积分)，因而关注点在等式右侧的积分过程。
  $$\begin{array}{rl}\mathcal{I}& ={\int }_{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]d{h}^{(i)}+{\int }_{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\log \left[\frac{\mathcal{Q}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(h^{(i)}\mid v^{(i)})}\right]d{h}^{(i)}\\ & =\underset{\text{Evidence of Lower Bound,ELBO}}{\underbrace{{\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left\{\log \left[\frac{\mathcal{P}(v^{(i)},h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]\right\}}}+\underset{\text{KL Divergence}}{\underbrace{\text{KL}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})||\mathcal{P}(h^{(i)}\mid v^{(i)})\right]}}\end{array}$$
  可以将$\text{ELBO}$继续向下分解，得到如下形式：
  $$\begin{array}{rl}\mathcal{I}& ={\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\log \mathcal{P}(v^{(i)},h^{(i)})-\log \mathcal{Q}(h^{(i)}\mid v^{(i)})\right]+\text{KL}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})||\mathcal{P}(h^{(i)}\mid v^{(i)})\right]\\ & ={\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\log \mathcal{P}(v^{(i)},h^{(i)})\right]\underset{\mathcal{H}[\mathcal{Q}(h^{(i)}\mid v^{(i)})];\text{Entropy}}{\underbrace{-{\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})\right]}}+\text{KL}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})||\mathcal{P}(h^{(i)}\mid v^{(i)})\right]\end{array}$$

• 最终，对数似然函数$\log \mathcal{P}(\mathcal{V})$可表示为：
  $$\begin{array}{rl}\log \mathcal{P}(\mathcal{V})& =\sum _{i=1}^N\mathcal{I}\\ & =\sum _{i=1}^N\left\{{\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\log \mathcal{P}(v^{(i)},h^{(i)})\right]\underset{\mathcal{H}[\mathcal{Q}(h^{(i)}\mid v^{(i)})];\text{Entropy}}{\underbrace{-{\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})\right]}}+\text{KL}\left[\mathcal{Q}(h^{(i)}\mid v^{(i)})||\mathcal{P}(h^{(i)}\mid v^{(i)})\right]\right\}\end{array}$$
  根据极大似然估计，将推断任务：求解$\mathcal{P}(h^{(i)}\mid v^{(i)})$转换为了：

  • 使用$\mathcal{Q}(h^{(i)}\mid v^{(i)})$替代了$\mathcal{P}(h^{(i)}\mid v^{(i)})$；
  • 选择合适的$\mathcal{Q}(h^{(i)}\mid v^{(i)})$来优化目标函数，使得目标函数$\text{ELBO}=\mathcal{L}\left[v^{(i)},h^{(i)},\mathcal{Q}(h^{(i)}\mid v^{(i)})\right]$达到最大：
    $$\underset{\mathcal{Q}(h^{(i)}\mid v^{(i)})}{\mathrm{argmax}}\mathcal{L}\left[v^{(i)},h^{(i)},\mathcal{Q}(h^{(i)}\mid v^{(i)})\right]$$

相关参考：
(系列二十五)近似推断2-推断即优化