摘要： 训练是构建神经网络模型的一个关键环节，该过程对网络中的参数不断进行微调，优化模型在训练数据集上的损失函数。参数初始化是训练之前的一个重要步骤，决定了训练过程的起点，对模型训练的收敛速度和收敛结果有重要影响。多层感知机是一种被广泛使用的经典神经网络模型，本文针对多层感知机上的区间随机初始化方法展开了深入调查，通过对前人成果的分析和总结得到了一种改良的初始化方法，并对所得方法进行了对比实验。

关键词： 多层感知机；参数初始化

---

引言

神经网络已经在各行各业的人工智能应用中得到了广泛应用，其构建过程需要在大量的数据上进行训练，对神经网络模型内部的参数进行微调，使得网络在训练集上的输出达到或接近某个损失函数的最优值——从本质上来说，神经网络的训练过程就是对一个参数量十分巨大的非凸函数的优化过程。训练过程常用的优化算法有随机梯度下降 (SGD)、RMSprop[1]、Adam[2] 等。

无论使用哪种优化算法，在训练之前都要对网络中的参数赋予初值。从非凸优化的角度看，初值决定了优化过程的起点，对模型的训练过程有重要影响，例如，如果简单地将模型中的参数初始化为相同的值，那么训练过程就无法继续[3]。一个好的初值能够大大提高训练速度，同时减少陷入局部最优的可能性，反之，一个糟糕的初值则可能会带来梯度消失、梯度爆炸等问题。图 1 是 Narkhede 等人对当前
所有初始化方法的分类[4]，在这些方法中，区间随机初始化是最基本、最常用的方法，表 1 列出了目前主流框架初始化全连接层的默认方式，可见大部分都采用了均匀随机初始化方法。

多层感知机 (MLP) 是一种经典的神经网络，常被用于分类和回归任务，同时也是许多高级神经网络模型的基础结构。本文跟随 Narkhede 综述的指引，对 MLP 上的区间随机初始化方法展开了深入调查。由于理论上一个足够宽的三层感知机能拟合任意复杂的连续函数[11-12]，所以很多方法都针对三层感知机提出，[13-21] 但是实际应用中仍然会使用超过三层的结构，因此有必要将三层感知机上的初始化方法推广到有更多层的感知机上。本文总共调查了 8 种初始化方法（以论文第一作者命名）：Nguyen[13]、Mittal[18]、Halawa[22]、Yam[16]、Drago[15]、Wessels[17]、Sodhi[20]、Qiao[19]，在理解和分析的基础上总结得到了一种适用于多输入、多输出、多层次 MLP 的改良初始化方法，并开展了数值实验。

本文的内容编排如下：第二节介绍三层 MLP，约定本文使用的记号，综述了 8 种初始化方法；第三节给出本文的初始化方法并详细说明了原理；第四节对所得方法开展了数值实验；第五节是对全文的总结。

三层感知机及其初始化

本文后续讨论使用的符号主要基于三层 MLP。三层 MLP 由输入层、隐藏层、输出层组成： 设三层的神经元数量分别为 $I$、$J$、$K$；输入层神经元的输出为 $x_1,x_2,\dots ,x_I$；隐藏层神经元的输入为 $t_1,t_2,\dots ,t_J$，输出为 $h_1,h_2,\dots ,h_J$； 输出层神经元的输入为 $y_1,y_2,\dots ,y_J$；第 $i$ 个输入层神经元到第 $j$ 个隐藏层神经元的权重为 $w_{ij}$；第 $j$ 个隐藏层神经元的偏置为 $b_j$； 第 $j$ 个隐藏层神经元到第 $k$ 个输出层神经元的权重为 $w_{jk}$；第 $k$ 个输出层神经元的偏置为 $d_k$。

三层 MLP 从输入到输出的变换过程可以表达为：$$\begin{array}{rl}{t}_j& =\sum _{i=1}^I(w_{ij}{x}_i)+b_j\\ h_j& =f(t_j)\\ y_k& =\sum _{j=1}^J(v_{jk}{h}_j)+d_k\end{array}$$ 其中 $f$ 为非线性的激活函数，尽管近年来出现了 ReLU、ELU、Softmax 等新的激活函数，遵照传统，本文还是选择了 sigmoid 函数 $\sigma (x)={(1+\exp (-x))}^{-1}$。

下面综述本文调研的 8 种初始化方法。

• Nguyen
  Nguyen 和 Widrow 在 1990 年提出的方法是商业数学软件 Matlab 神经网络工具箱的默认初始化方法[23] ，也被后续很多工作标的和改良。该方法针对多输入单输出的 MLP 拟合任务提出，其核心思想是用隐藏层神经元输出的 sigmoid 线性区域均匀地覆盖整个输入空间从而加速训练，尽管原文关于方法推导的描述略微复杂，其最终初始化方法却很简单，对于每个隐藏层神经元 $j\in [0,J]$：

  $$\begin{array}{rl}{\omega }_{ij}& =U(-1,1)\\ w_{ij}& =0.7\cdot J^{\frac{1}{I}}\cdot \frac{{\omega }_{ij}}{\sqrt{{\sum }_{i=i}^I{\omega }_{ij}^2}}\\ b_j& =J^{\frac{1}{I}}\cdot U(-1,1)\end{array}$$

  公式中常数 0.7 意在使不同隐藏层神经元的 sigmoid 函数输入区间 $[-1,1]$ 在放缩后能由部分重叠，这是一个经验值，文章称这样往往能取得较好结果。

  隐藏层到输出层的初始化方法文章没有给出，文中权重向量模长的选取方法存在瑕疵，并且文中所得结论不能直接推广到多输出的 MLP。最后，值得一提的是，这篇文章中使用的三层 MLP 输出层并不包含偏置参数。

• Mittal
  Mittal 将 Nguyen 方法推广到了多层 MLP 。他的方法将多层 MLP 的前一个隐藏层看作是后一个隐藏层的输入层，然后在这辆层之间重复套用 Nguyen 的分析。Mittal 注意到了 Nguyen 方法中权重模长选取的缺陷：当隐藏层很宽时（$J$很大），隐藏层神经元的输入会偏向饱和区，其修正后的初始化方法如下：

  $$\begin{array}{rl}{\omega }_{ij}& =U(-1,1)\\ w_{ij}& =0.7\cdot a\cdot \frac{{\omega }_{ij}}{\sqrt{{\sum }_{i=i}^I{\omega }_{ij}^2}}\\ b_j& =J^{\frac{1}{I}}\cdot U(-1,1)\end{array}$$

  其中 $a$ 是一个常数，论文在 9 个任务上对 1 到 10 的十个整数进行了尝试，得到 $a$ 的最优取值为 4。

• Halawa
  Halawa 的方法使用对训练集的分析改进了 Nguyen 方法中神经元的散布，从而有效地降低了训练时间并且提升了训练效果。

  其具体做法为将输入空间均匀切分为 $N$ 块超立方体区域（$N$ 为先验指定的一个值），然后对训练集进行分析，统计落入每个区域输入的的标准差，然后按比例将一半的隐藏层神经元分配到这些区域上。然后对每块区域分别使用 Nguyen 方法初始化，但这时候因为已经得到了每个区域内输入的标准差，初始化区间可以得到改良。

  对于每个区域，设区域内分配 $S$ 个神经元，对于任意的神经元 $s\in [0,S]$：

  $$\begin{array}{rl}{\omega }_{is}& =U(-1,1)\\ w_{is}& =0.7\cdot S^{\frac{1}{I}}\cdot \frac{{\omega }_{ij}}{\sqrt{{\sum }_{i=i}^I{\omega }_{ij}^2}}\\ b_j& =-[w_{1s},w_{2s},\dots ,w_{Is}]\cdot \mathbf{p}\end{array}$$
  式中 $\mathbf{p}$ 为这块超立方体内均匀随机选择的一个 $I$ 维点向量。

  文章同样没有给出隐藏层到输出层的初始化方法。

• Yam
  Yam 的方法意在确保在训练的开始阶段，所有训练样本都能使得每层神经元的输入位于 sigmoid 的活跃区域：$[-4.36,4.36]$，这是通过对训练集做整体的统计分析，求得样本输入间的最大距离 $D^{in}=\sqrt{{\sum }_{i=1}^N(\max (x_i)-\min (x_i){)}^2}$ 做到的。在初始化第二层 以外的隐藏层时，由于 sigmoid 函数的值域为 $(0,1)$，因此可以直接确定 $D^{In}$。具体公式如下：
  $$\begin{array}{rl}{w}_{ji}& =\frac{8.72}{D^{in}}\sqrt{\frac{3}{I}}\cdot U(-1,1)\\ b_j& =-\sum _{i=1}^N\left(w_{ji}\cdot \frac{\max (x_i)+\min (x_i)}{2}\right)\\ v_{jk}& =\frac{15.10}{J}\cdot U(-v_{max},v_{max})\\ d_k& =-0.5\sum _{j=1}^J{v}_{jk}\end{array}$$

  该方法逻辑简单，所给出的分析也比较可靠，文中和 Nguyen、Drago 等方法开展了实验对比，取得了更快的训练速度。

• Drago
  Drago 的方法为初始化问题提供了一种独特的思路。其认为初始化结果和训练过程中神经元"麻痹"比例的统计量（文中称之为 PNP）之间存在关联。 所谓"麻痹"是指在一个采用 sigmoid 作为激活函数的 MLP 中，对于某个样本，MLP 中神经元的输入处于 sigmoid 的活跃区之外，并且此时的输 出和样本标签差别较大。

  显然这个 PNP 是一个后验量，必须要在整个训练集上对已经初始化好的 MLP 进行测试才能得到，因此为了能让其用于初始化，论文对训练过程做了很多假设，比如"隐藏层神经元的输入满足中心极限定理"、"未训练的 MLP 输出向量每个维度的正确概率为0.5"等，然后基于这些假设进行了概率分析，得到了如下的初始化公式：

  $$\begin{array}{rl}R& =\frac{\sqrt{3}}{{\mathrm{erf}}^{-1}(0.5-\frac{0.5}{1-0.5^K}\cdot PNP)}\\ w_{ij},b_j& =\frac{R\cdot a_0}{\sqrt{{\sum }_{i=1}^{I}E(x_i^2)}}\cdot U(-1,1)\end{array}$$
  然后，论文开展了实验确定 PNP 的最优值大约为 5%，需要说明的是这个值和训练过程的优化方法和激活函数都有关，因此这种方法有很大的局限性。

• Wessels
  Wessels 的论文中给出了用于对比分析的普通小区间均匀随机初始化方法：

  $$\begin{array}{rl}{w}_{ij}& =-\frac{3a}{\sqrt{I}}\cdot U(-1,1)\\ b_j& =0\end{array}$$

  式中 $a$ 在预实验后确定位最优值 1 用于对比实验。Wessels 对该普通方法进行了概率分析，然后提出了他们自己的方法。

  注意到每个隐藏层神经元实质上是用一个 $I$ 维超平面 ${\sum }_{i=1}^I(w_{ij}{x}_i)=b_j$ 将输入空间划分为两部分，该超平面由 $w_{ij}$ 和 $b_j$ 共同确定。假设输入归一化到$[0,1]$之间，则输入空间是边长为 1 的超立方体，将这个超平面改用以这个超立方体中心为原点的极坐标表示，通过均分角度把超平面均匀朝向各个方向，然后将超平面的距离依次为 $\frac{1}{2^j}j\in [1,J]$，这样就确定了 $w_{ij}$。$b_j$ 通过确保超立方体边角对应的输入值位于 sigmoid 函数的活跃区间内确定，即 $b_j=\min (4.36,{\sum }_{i=1}^I{w}_{ij})$。最后，论文坦言没有好的方法设置输出层的参数，因此简单地将 $v_{jk}$ 统一置为 $1$，$d_k$ 置为0。

  从本质上来说，Wessels 的方法和 Nguyen 在"把隐藏层神经元对应处理的区域散布到输入空间中去"这一点上是一致的，Wessels 从超平面的角度进行了 分析，而 Nguyen 则是从区间拟合的角度看待这个问题。两者只是在散布的方式上有所差异：Nguyen 的方法会在输入空间中产生真正均匀分布的超平面，而 Wessel 方法散布的超平面会更聚集在输入空间的中心位置。

  论文只在 $I=2$ 的 MLP 上进行了讨论和实验，然而如果尝试将论文的方法推广到更高维度的输入就会遇到困难。问题在于高维空间中生成均匀分布的方向向量并不是一件容易的事，将角度形式的方向向量转换为笛卡尔坐标系的权重向量也比较麻烦，且在高维空间中没有超平面覆盖到的边角区域会进一步扩大，这可能会降低实际使用的效果。

• Sodhi

  Sodhi 的方法只是对普通简单区间随机初始化方法的改良。其从 $I$ 维权重向量构成的 $I$ 维超立方体空间的对角线上切割出 $J$ 个小正方体，然后将 $J$ 个隐藏层神经元的参数分别在这些小正方体里随机初始化：

  $$\begin{array}{rl}{w}_{ij}& =\frac{\lambda j}{J}\cdot U(0,1)\\ b_j& =U(-0.5,0.5)\\ v_{jk}& =U(-0.5,0.5)\\ d_k& =0\end{array}$$

  其中 $\lambda$ 是一个实验测定参数，文中测试了 $0.25$，$0.50$，$0.75$，$1.00$ 四个取值，确定最优取值为 $\lambda =1$。

  对于该方法的合理性，文中没有做太多的理论分析，而是采用了大量数值实验证明其有效性，其结果表明该方法优于简单的区间随机初始化。

• Qiao

  Qiao 方法受到 Talaska[24] 的启发，认为训练过程的全局最优点应该能反映输入和输出之间的互信息，因此他们对测试集进行了分析，求得互信息（$MI$）来确定区间初始化的范围，在 $MI$ 确定之后，使用如下的公式初始化模型参数：

  $$\begin{array}{rl}{w}_{ij},b_j& =\max (0.5,\frac{4.36}{I(I+1)\cdot \frac{\max (MI)}{{\sum }_{i=1}^{I}MI(i)}-I+1})\cdot U(-1,1)\\ v_{jk},d_k& =U(-1,1)\end{array}$$

  其中 $MI$ 的计算过程比较复杂，出于篇幅原因不在此具体介绍。

  虽然该方法出发点是"让模型中参数反映输入和输出之间的关系"，但其最终的公式设计受到了其它很多因素影响，可以看出其方法实质上仍然是采用均匀随机分布初始化，对数据集的分析只是用于确定初始化的区间范围，从初始化结果来说，也很难说模型参数和训练集的互信息量之间存在什么联系。论文和 Yam 等人的方法进行了对比，由于该方法计算过程比较复杂，其初始化时间显著高于其它方法，但取得了损失更低的训练结果。

---

改良的初始化方法

我分析了上述前人的方法，对它们加以总结得到了一个改良的初始化方法。我们在无法对训练数据进行预分析时，如下方式初始化各层参数：

$$\begin{array}{r}\begin{array}{rl}{P}_i& =U(0,1)\\ Q_i& =N(0,1)\\ w_{ij}& =-\frac{8.41}{I}\cdot \frac{Q_i}{\sqrt{{\sum }_{i=1}^I{Q}_i^2}}\\ b_j& =\frac{8.41}{I}\cdot \frac{{\sum }_{i=1}^I(Q_i{P}_i)}{\sqrt{{\sum }_{i=1}^I{Q}_i^2}}\end{array}\end{array}$$

当有条件对训练数据进行预分析时，我们可以用预分析进一步做出改善，具体方法在 3.3节中说明。

和前人一样，我们也假设 MLP 输入的每一维都被归一化到区间 $[0,1]$ 之间。为了对该方法的原理进行解释，下面首先对隐藏层神经元输入进行概率分析，然后再介绍该方法背后的原理。

隐藏层神经元输入的概率分析

用 $E$ 表示随机变量的期望，对于隐藏层每个神经元的输入 $t_j$：

$$\begin{array}{r}E(t_j)=\sum _{i=1}^{I}E(w_{ij}{x}_i)+E(b_j)\end{array}$$

显然 $x_i$ 和 $w_{ij}$ 相独立，且初始化时所有的 $w_{ij}$ 都独立同分布，所以：

$$\begin{array}{rl}E(t_j)& =\sum _{i=1}^I(E(w_{ij})\cdot E(x_i))+E(b_j)\\ & =E(w_{ij})\cdot \sum _{i=1}^{n}E(x_i)+E(b_j)\end{array}$$

现在再考虑输入的方差，用 $D(x)$ 表示 $x$ 的方差，则：

$$\begin{array}{r}D(t_j)=E(t_j^2)-E^2(t_j)\end{array}$$

对于所有激活函数，$0$ 附近都是函数值变化最活跃的区域，尤其是对于 sigmoid 类型的激活函数而言，过大或过小的输入都会发生梯度消失问题。因此实际都会设计方法使得 $E(t_j)=0$，所以：

$$\begin{array}{c}D(t_j)=E(t_j^2)=E\left(b_j^2+2b_j\cdot \sum _{i=1}^I(x_i\cdot w_{ij})+\sum _{a,b=1}^I(x_a{w}_{aj}\cdot x_b{w}_{bj})\right)\\ =E(b_j^2)+2\cdot E(b_j)E(w_{ij})\sum _{i=0}^{I}E(x_i)\\ +E^2(w_{ij})\sum _{\begin{array}{c}a,b=1\\ a\ne b\end{array}}^{I}E(x_a{x}_b)+E(w_{ij}^2)\cdot \sum _{i=1}^{I}E(x_i^2)\end{array}$$

如果我们选择的 $w$ 的分布满足 $E(w)=0$（比如$U(-1,1)$），则：

$$\begin{array}{r}D(t_j)=E(b_j^2)+E(w_{ij}^2)\cdot \sum _{i=1}^{I}E(x_i^2)\end{array}$$

如果我们选择的 $b$ 的分布也满足 $E(b)=0$，这时可以进一步得到：

$$\begin{array}{r}D(t)=D(b_j)+D(w_{ij})\cdot \sum _{i=1}^{I}E(x_i^2)\end{array}$$

由于 $x_i$ 的概率分布是未知的，我们无法预知它经过一个非线性激活函数后的方差和期望，为了不让我们的分析止步于此，下面我们假设所有的 $x_i$ 都 独立同分布，则隐藏层神经元输入的的方差和期望变成：

$$\begin{array}{r}E(t)=E(b)+I\cdot E(w)E(x)\\ D(t)=E(b^2)+I\cdot E(w^2)E(x^2)\end{array}$$

在不知道具体的 $I$ 是多少时，我们还是不知道输入层神经元的输入是如何分布的，所以我们再假设 $I$ 足够大以至于满足中心极限定理，由于假设要求条件太强，这样的分析只有参考价值，我们的目的在于观察输出的分布。这时 $t$ 符合正态分布：$t\sim N(E(t),\sqrt{D(t)})$，在确定了激活函数后，我们就可以将分析拓展到输出层。下面我们选择了 sigmoid 激活函数，则隐藏层神经元的输出的概率密度函数为：

$$f(h)=\frac{\sqrt{2}{e}^{-\frac{{\left(-E(t)-\log \left(-1+\frac{1}{h}\right)\right)}^2}{2D(t)}}\left|\frac{1}{h^2\cdot \left(1-\frac{1}{h}\right)}\right|}{2\sqrt{\pi }\sqrt{D(t)}}$$

该函数只在 $(0,1)$ 区间有定义，对于如此复杂的函数，我们不可能求得期望和方差的符号解，只能通过数值方式求取近似值，图 2 是它的形状。

从图上可以明显看出，使用 sigmoid 函数的隐藏层会使得数据向中心收缩，彻底改变输入原有的分布特征。

本文方法的原理

这里本文采用用 Wessels 的超平面视角来对方法的原理进行阐释：对于每一个隐藏层神经元，其权重 $w_{ij}$ 和 $b_j$ 确定了一个 $I$ 维空间的超平面 ${\sum }_{i=1}^I(w_{ij}{x}_i)=b_j$，这个超平面将输入空间划分为两部分，落入两侧的输入分别使得神经元兴奋和静息，$W_j=[w_{1}j,w_{2}j,\dots ,w_{I}j]$ 就是这个超平面的法向量，而超平面到原点的距离即为 $\frac{b_j}{|W_j|}$，如图 3。

初始化 $w_{ij}$ 和 $b_j$ 就是确定 $J$ 个超平面的位置，在没有关于训练样本的额外信息的情况下，我们只能认为输入样本可能分布在空间的任何位置，或者说任何位置都有可能需要一个超平面进行划分，因此我们应当使得超平面尽可能均匀地分布在输入空间。为了做到这一点，在输入空间内随机选择一个点 $P\in [0,1{]}^I$ 作为超平面的必经点，然后再确定一个方向向量 $Q\in [0,1{]}^I$ 作为超平面的法向量，这样一个超平面就确定好了， 如果 $P$ 和 $Q$ 的选取是均匀随机的，那么超平面的分布就是均匀的。

很容易做到 $P$ 的选取是均匀随机的，只需要给 $P$ 的每一维都赋予一个 $[0,1]$ 上的均匀随机数即可，即 $P_i\sim U(0,1)$。$Q$ 的均匀选取要求我们在高维空间里均匀随机地挑选一个方向，这可以通过让 $Q$ 的每一维都符合正态分布得到，即$Q_i\sim N(0,1)$，下面证明这样构造的向量在方向选取上是均匀的：

设 $Q_i$ 的密度函数为 $\varphi (x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$，分布函数为 $\Phi (x)$， 对于 $I$ 维空间中位于 $[x_0,x_1,\dots ,x_I]$ 、边长 $\mathrm{d}x$ 的一个体积元，$Q$ 分布在其中的概率为：

$$P=\prod _{i=1}^I(\Phi (x_i+\mathrm{d}x)-\Phi (x_i))$$

当 $\mathrm{d}x\to 0$ 时：

$$P=\prod _{i=1}^I\varphi (x_i)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{\sum }_i^I(x_i^2)}{2}}=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{{|Q|}^2}{2}}$$

可见 $P$ 只与 $Q$ 的模长，即距离原点的距离有关，所以 $Q$ 在方向上的分布是均匀的。

如图 3 所示， $P$、$Q$ 和 $W_j$、$b_j$ 的关系为：

$$\begin{array}{rl}\frac{W_j}{|W_j|}& =\frac{Q}{|Q|}\\ \frac{Q}{|Q|}\cdot P& =-\frac{b_j}{|W_j|}\end{array}$$

从公式可知，在选取了 $P$ 和 $Q$ 后，我们还需要进一步确定 $\frac{|W_j|}{|Q|}$（记为 $\alpha$）：

$$\begin{array}{c}\begin{array}{r}\begin{array}{rl}{W}_j& =|W_j|\cdot \frac{Q}{|Q|}=\alpha \cdot Q\\ b_j& =-|W_j|\cdot \frac{Q}{|Q|}\cdot P=-\alpha \cdot Q\cdot P\end{array}\end{array}\end{array}$$

这时上一小节的概率分析就派上了用场。

首先需要确认目前的 $W_j$ 和 $b_j$ 初始化满足上一小节分析的要求：$E(t_j)=0$：

对于 $w_{ij}$，由于 $W_j=|W_j|\cdot Q_i$ 而 $Q$ 的每个维度符合正态分布 $N(0,1)$，所以 $E(w_{ij})=0$； 对于 $b_j$：

$$\begin{array}{r}E(b_j)=E(\alpha \cdot Q\cdot P)=-\alpha \cdot \sum _{i=1}^{I}E(Q_i{P}_i)\\ =-\alpha \cdot \sum _{i=1}^{I}E(Q_i)E(P_i)=0\end{array}$$

所以 $E(t_j)=E(w_{ij})\cdot {\sum }_{i=1}^{n}E(x_i)+E(b_j)=0$。

所以，这时隐藏层神经元的输入方差:

$$\begin{array}{c}\begin{array}{r}\begin{array}{rl}D(t_j)& =D(b_j)+D(w_{ij})\cdot \sum _{i=1}^{I}E(x_i^2)\\ & =-\alpha \sum _{i=1}^I(D(Q_i)D(P_i))+\alpha D(Q_i)\cdot \sum _{i=1}^{I}E(x_i^2)\\ & =-\alpha \frac{I}{12}+\alpha \sum _{i=1}^{I}E(x_i^2)\end{array}\end{array}\end{array}$$

由于此前分散超平面时我们已经认为输入均匀地分散在输入空间，所以 $x_i\sim U(0,1)$，那么 $E(x_i^2)=\frac{1}{3}$，所以：

$$\begin{array}{r}D(t_j)=-\alpha \frac{I}{4}\end{array}$$

我们希望这个 $D(t_j)$ 不要太大，例如对于 sigmoid 函数而言，我们希望输入最好能落在它的活跃区间 $[-4.36,4.36]$，所以我们根据 3$\sigma$ 准则限制 $t_j$ 的标准差为 $\frac{4.36}{3}\approx 1.45$，那么 $D(t_j)=1.45^2$，所以 $\alpha \approx -\frac{8.41}{I}$，对应的 $|W_j|$ 为：

$$\begin{array}{r}|W_j|=\alpha \cdot |Q|=-\frac{8.41}{I}\cdot |Q|\end{array}$$

所以我们得到了最终的初始化公式：

$$\begin{array}{r}\begin{array}{rl}{W}_j& =-\frac{8.41}{I}\cdot \frac{Q}{|Q|}\\ b_j& =\frac{8.41}{I}\cdot \frac{Q}{|Q|}\cdot P\end{array}\end{array}$$

对于多层 MLP，本方法和 Mittal[18] 一样将前层神经元的输出看作是输入，重复套用上述的分析方法 初始化后一层的 $w_{ij}$ 和 $b_i$。sigmoid 函数的值域为 $(0,1)$，满足上述分析中对输入空间的假设，但样本点不再满足均匀分布，这点差异对上述分析方法造成的影响是后一层神经元的输入会向 $[-4.36,4.36]$ 区间的中心（即 $0$）聚集，所以当层数很深的时候不会带来梯度消失或爆炸问题，只是会导致训练速度没有达到最优，仍然有优化的空间。

因此，本文下面进一步探讨使用对训练集的预分析来改进初始化的办法。

预分析训练集以改进初始化

上述的方法中假设输入数据均匀分布在 $[0,1{]}^I$ 空间内，如果条件允许，我们可以对模型的训练集进行预分析以消除这种假设。这里我们直接对整个输入空间进行分析，而没有采用 Halawa[22] 将输入空间划分为小区域的做法，因为对于中间的隐藏层而言，输入空间维数可能特别高，我们很难确定应该在哪些维度上划分小区域，而如果所有维度上都划分区域则会导致区域数出现指数爆炸。

由于这时的 $E(x_i^2)$ 可以根据训练集中的样本直接计算出来直接带入式(2)，所以这时的 $|W_j|$ 变成：

$$\begin{array}{r}|W_j|=\frac{2.1025}{{\sum }_{i=1}^{I}E(x_i^2)-\frac{I}{12}}\cdot |Q|\end{array}$$

然后带入式 (1)即可得到对应的初始化公式。

对于多层的情况，我们可以在前一层初始化好之后将训练数据带入求出输出集，再对这个输出集重复预分析过程来初始化下一层。虽然看起来这么做非常复杂，但从训练过程总体上看，它实际上并没有产生额外的计算量，因为这实际上是将训练过程的第一次前向传播过程提前到初始化阶段，因此是可以接受的。

---

实验与分析

本文使用 PyTorch 在两个任务上对所得方法展开了实验。

第一个任务是使用一个三层 MLP 在区间 $[0,1]$ 之间拟合函数 $f(x)=1000\frac{\sin (10\pi x)}{\pi x}$，隐藏层宽度为 100，使用RMSprop 算法进行优化，图 4 展示了训练过程的损失变化和训练结果，其中 default 指 PyTorch 默认的初始化方式，nodata 是无预分析的初始化方法， data 是使用预分析改进的方法。从图中可见相比于默认初始化方式，本文得到的方法确实能提高训练速度，改善训练结果，且使用预分析的效果要更优。

第二个任务是使用一个三层 MLP 在区间 $[0,1{]}^3$ 之间拟合函数

$$f([x_0,x_1,x_2])=100\ast [\frac{\sin (10\pi \cdot x_0)}{x_1}+x_2,(x_0+x_1+x_2{)}^3,\tan (x_0\cdot x_1\cdot x_2)]$$

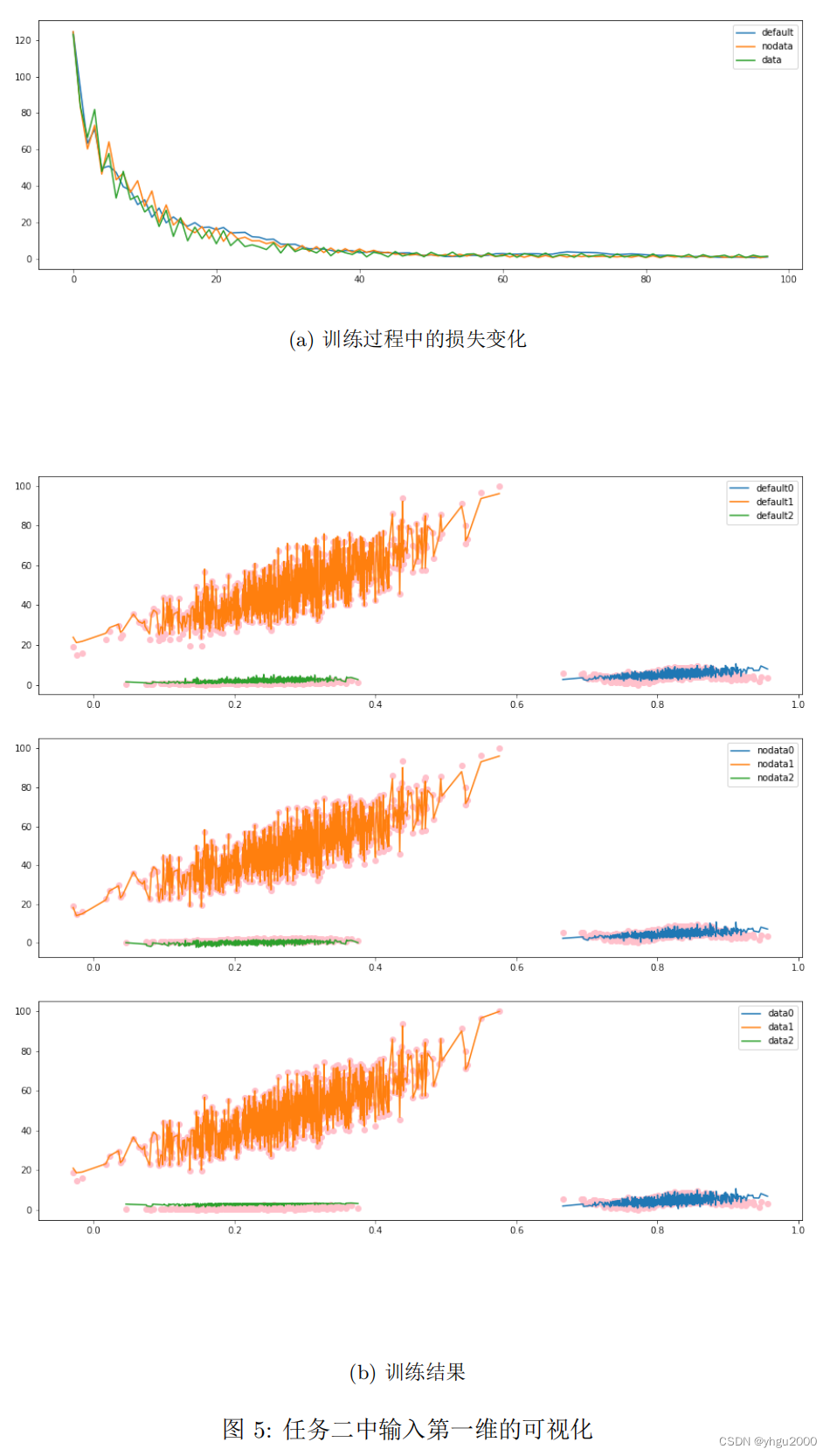
隐藏层宽度为 300，使用 RMSprop 算法进行优化，图 5 对输入的第一维进行可视化，展示了训练过程的损失变化和训练结果，其中图例含义和图 4 相同。虽然很遗憾，但是不得不承认我们并没有在图中观察到本文方法有很明显的优势，因此本文方法拓展到多维场景下的有效性还需要进一步论证。

我还没有完成该方法在多隐藏层 MLP 上的实验，因为目前还没能设计和构建一个能收敛的多层 MLP 任务，这是本文工作的一个缺陷，也许有生之年我会尝试解决这个问题。

总结

多层感知机是一种重要的神经网络结构，本文对多层感知机上的区间随机初始化方法进行了深入调研，在对前人方法总结分析后得到了一种改良的区间随机初始化方法。本文方法相较前人的改良点在于：

1. 改进了神经元超平面在输入空间的散布，使其更加均匀；
2. 通过将第一次前向传播过程提前到初始化阶段，将训练集预分析推广到多层 MLP；
3. 除了 3$\sigma$准则和 sigmoid 的活跃区间 $[-4.36,4.36]$ 的选取之外，没有任何先验参数；
4. 基于很少的假设条件，理论基础和逻辑性更好

参考文献

1. GRAVES A. Generating Sequences With Recurrent Neural Networks: arXiv:1308.0850[M/OL]. arXiv, 2014[2022-12-10]. http://arxiv.org/abs/1308.0850. DOI: 10.48550/arXiv.1308.0850.
2. KINGMA D P, BA J. Adam: A Method for Stochastic Optimization: arXiv:1412.6980[M/OL]. arXiv, 2017[2022-12-10]. http://arxiv.org/abs/1412.6980. DOI: 10.48550/arXiv.1412.6980.
3. RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J/OL]. Nature, 1986, 323(6088): 533-536. https://doi.org/10.1038/323533a0.
4. NARKHEDE M V, BARTAKKE P P, SUTAONE M S. A review on weight initialization strategies for neural networks[J/OL]. Artificial Intelligence Review,2022, 55(1): 291-322. DOI: 10.1007/s10462-021-10033-z.
5. Linear —PyTorch 1.13 documentation[EB/OL]. [2022-12-10]. https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear.
6. Tf.keras.initializers.GlorotUniform | TensorFlow v2.11.0[EB/OL]. TensorFlow [2022-12-10]. https://www.tensorflow.org/api_docs/python/tf/keras/initializers/GlorotUniform.
7. Initialization —Apache MXNet documentation[EB/OL]. [2022-12-10]. https://mxnet.apache.org/versions/1.6/api/python/docs/tutorials/packages/gluon/blocks/init.html.
8. MAHILLEB msft. Cntk.layers.layers module[EB/OL]. [2022-12-10]. https://learn.microsoft.com/en-us/python/api/cntk/cntk.layers.layers.
9. Linear-API 文档-PaddlePaddle 深度学习平台[EB/OL]. [2022-12-10]. https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/nn/Linear_cn.html.
10. MindSpore[EB/OL]. [2022-12-10]. https://www.mindspore.cn/docs/zh-CN/r1.9/api_python/nn/mindspore.nn.Dense.html#mindspore.nn.Dense.
11. FUNAHASHI K I. On the approximate realization of continuous mappings by neural networks[J/OL]. Neural Networks, 1989, 2(3): 183-192[2022-12-10]. https://www.sciencedirect.com/science/article/pii/0893608089900038. DOI: 10.1016/0893-6080(89)90003-8.
12. HORNIK K, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators[J/OL]. Neural Networks, 1989, 2(5): 359-366[2022-12-10]. https://www.sciencedirect.com/science/article/pii/0893608089900208.DOI: 10.1016/0893-6080(89)90020-8.
13. NGUYEN D, WIDROW B. Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights[C/OL]//1990: 21-26 vol.3. DOI: 10.1109/IJCNN.1990.137819.
14. DOLEZEL P, SKRABANEK P, GAGO L. Weight Initialization Possibilities for Feedforward Neural Network with Linear Saturated Activation Functions[J/OL]. IFAC-PapersOnLine, 2016, 49(25): 49-54. DOI: 10.1016/j.ifacol.2016.12.009.
15. DRAGO G P, RIDELLA S. Statistically controlled activation weight initialization (SCAWI)[J/OL]. IEEE Transactions on Neural Networks, 1992, 3(4):627-631. DOI: 10.1109/72.143378.
16. YAM J Y F, CHOW T W S. Feedforward networks training speed enhancement by optimal initialization of the synaptic coefficients[J/OL]. IEEE Transactions on Neural Networks, 2001, 12(2): 430-434. DOI: 10.1109/72.914538.
17. WESSELS L F A, BARNARD E. Avoiding false local minima by proper initialization of connections[J/OL]. IEEE Transactions on Neural Networks, 1992, 3(6): 899-905. DOI: 10.1109/72.165592.
18. MITTAL A, SINGH A P, CHANDRA P. A Modification to the Nguyen–Widrow Weight Initialization Method[C/OL]//Springer Singapore, 2020: 141-153. DOI:10.1007/978-981-13-6095-4_11.
19. QIAO J, LI S, LI W. Mutual information based weight initialization method for sigmoidal feedforward neural networks[J/OL]. Neurocomputing, 2016, 207:676-683. DOI: 10.1016/j.neucom.2016.05.054.
20. SODHI S S, CHANDRA P, TANWAR S. A new weight initialization method for sigmoidal feedforward artificial neural networks[C/OL]//2014: 291-298. DOI:10.1109/IJCNN.2014.6889373.
21. KIM Y K, RA J B. Weight value initialization for improving training speed in the backpropagation network[C/OL]//0018/1991: 2396-2401 vol.3. DOI: 10.1109/IJCNN.1991.170747.
22. HALAWA K. A New Multilayer Perceptron Initialisation Method with Selection of Weights on the Basis of the Function Variability[C/OL]//Springer International Publishing, 2014: 47-58. DOI: 10.1007/978-3-319-07173-2_5.
23. Initialize neural network - MATLAB init - MathWorks 中国[EB/OL]. [2022-12-12]. https://ww2.mathworks.cn/help/deeplearning/ref/network.init.html.
24. TALAśKA T, KOLASA M, DłUGOSZ R, et al. An efficient initialization mechanism of neurons for Winner Takes All Neural Network implemented in the CMOS technology[J/OL]. Applied Mathematics and Computation, 2015, 267: 119-138 [2022-12-13]. https://www.sciencedirect.com/science/article/pii/S0096300315025. DOI: 10.1016/j.amc.2015.04.123.

附录

实验代码

# %%
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn, optimfactor = 100class Net(nn.Module):def __init__(self, widthes: list[int]) -> None:super().__init__()self.widthes = widthesself.layers = [nn.Linear(I, K) for I, K in zip(widthes, widthes[1:])]for i in range(len(self.layers)):self.add_module(f"L{i}", self.layers[i])def forward(self, X: torch.Tensor):ite = iter(self.layers)layer = next(ite)try:while True:X = layer(X)layer = next(ite)X = torch.sigmoid(X)except StopIteration:passreturn X# for layer in self.layers:#     X = torch.sigmoid(layer(X))# return factor * Xdef myinit(self):with torch.no_grad():for layer in self.layers:I = layer.weight.shape[-1]for j in range(len(layer.weight)):P = torch.rand(I)Q = torch.normal(0, 1, [I])Q_norm = Q / torch.norm(Q)layer.weight[j, ...] = -8.41 / I * Q_normlayer.bias[j] = 8.41 / I * (Q_norm @ P)def myinit_with_data(self, data):with torch.no_grad():for layer in self.layers:I = layer.weight.shape[-1]J = len(layer.weight)sumExi2 = torch.sum(data * data) / len(data)Wj_normQ = 2.1025 / (sumExi2 - I / 12)for j in range(J):P = torch.rand(I)Q = torch.normal(0, 1, [I])Q_norm = Q / torch.norm(Q)layer.weight[j, ...] = Wj_normQ * Q_normlayer.bias[j] = -Wj_normQ * (Q_norm @ P)data = torch.sigmoid(layer(data))# %% 1I1O 拟合任务
f = lambda x: 1000 * torch.sin(10 * torch.pi * x) / torch.pi * x
fig = plt.figure(layout="constrained")
fig.set_size_inches(7.5, 5)xs = torch.sort(0.75 * torch.normal(0.1, 0.1, [1000])+ 0.25 * torch.normal(0.8, 0.2, [1000])
)[0]
Xs = xs.reshape([-1, 1])
Ys = f(Xs)
Xs_cuda, Ys_cuda = Xs.cuda(), Ys.cuda()criterion = nn.MSELoss()
netshape = [1, 100, 1]ax = fig.add_subplot()
ax.scatter(Xs.data, Ys.data, color="pink")net = Net(netshape)
optimizer = optim.RMSprop(net.parameters())
losses = []
ax.plot(xs, net(Xs).data, label="default")mynet = Net(netshape)
mynet.myinit()
myoptimizer = optim.RMSprop(mynet.parameters())
mylosses = []
ax.plot(xs, mynet(Xs).data, label="nodata")mydnet = Net(netshape)
mydnet.myinit_with_data(Xs)
mydoptimizer = optim.RMSprop(mydnet.parameters())
mydlosses = []
ax.plot(xs, mydnet(Xs).data, label="data")ax.legend()
fig.savefig("exp-1I1O_0.png")# %%
epoches = 10000net.cuda(), mynet.cuda(), mydnet.cuda()
for i in range(epoches):ys = net(Xs_cuda)loss = criterion(ys, Ys_cuda)loss.backward()optimizer.step()myys = mynet(Xs_cuda)myloss = criterion(myys, Ys_cuda)myloss.backward()myoptimizer.step()mydys = mydnet(Xs_cuda)mydloss = criterion(mydys, Ys_cuda)mydloss.backward()mydoptimizer.step()if i % 10 == 0:losses.append(float(loss.data))mylosses.append(float(myloss.data))mydlosses.append(float(mydloss.data))if i % (epoches // 10) == 0:print(losses[-1], mylosses[-1], mydlosses[-1])
net.cpu(), mynet.cpu(), mydnet.cpu()fig, ax = plt.subplots()
fig.set_size_inches(10, 5)
ax.plot(losses[-1500:], label="default")
ax.plot(mylosses[-1500:], label="nodata")
ax.plot(mydlosses[-1500:], label="data")
ax.legend()
fig.savefig("exp-1I1O_1.png")fig, ax = plt.subplots()
fig.set_size_inches(10, 5)
ax.scatter(xs, Ys.data, color="pink")
ax.plot(xs, net(Xs).data, label="default")
ax.plot(xs, mynet(Xs).data, label="nodata")
ax.plot(xs, mydnet(Xs).data, label="data")
ax.legend()
fig.savefig("exp-1I1O_2.png")# %% 3I3O 拟合任务
def f(X):x0 = X[..., 0]x1 = X[..., 1]x2 = X[..., 2]y = torch.empty_like(X)y[..., 0] = torch.sin(10 * torch.pi * x0) / torch.pi * x1 + x2y[..., 1] = (x0 + x1 + x2) ** 3y[..., 2] = torch.tan(x0 * x1 * x2)return yfig = plt.figure(layout="constrained")
fig.set_size_inches(7.5, 5)xs = torch.empty([1000, 3])
xs[..., 0] = 0.1 * torch.normal(0.1, 0.1, [1000]) + 0.9 * torch.normal(0.9, 0.05, [1000]
)
xs[..., 1] = 0.75 * torch.normal(0.1, 0.1, [1000]) + 0.25 * torch.normal(0.8, 0.2, [1000]
)
xs[..., 2] = 0.9 * torch.normal(0.2, 0.05, [1000]) + 0.1 * torch.normal(0.5, 0.3, [1000]
)Xs = xs.reshape([-1, 3])
Ys = f(Xs)
Ys_max = torch.max(Ys)
Ys_min = torch.min(Ys)
Ys = factor * (Ys - Ys_min) / (Ys_max - Ys_min)
Xs_cuda, Ys_cuda = Xs.cuda(), Ys.cuda()criterion = nn.MSELoss()
netshape = [3, 300, 3]ax = fig.add_subplot()
ax.scatter(Xs.data, Ys.data, color="pink")xs0si = torch.sort(xs[..., 0])[1]
xs1si = torch.sort(xs[..., 1])[1]
xs2si = torch.sort(xs[..., 2])[1]net = Net(netshape)
optimizer = optim.RMSprop(net.parameters())
losses = []
ax.plot(xs[..., 0][xs0si], net(Xs).data[..., 0][xs0si], label="default0")
ax.plot(xs[..., 1][xs1si], net(Xs).data[..., 1][xs1si], label="default1")
ax.plot(xs[..., 2][xs2si], net(Xs).data[..., 2][xs2si], label="default2")mynet = Net(netshape)
mynet.myinit()
myoptimizer = optim.RMSprop(mynet.parameters())
mylosses = []
ax.plot(xs[..., 0][xs0si], mynet(Xs).data[..., 0][xs0si], label="nodata0")
ax.plot(xs[..., 1][xs1si], mynet(Xs).data[..., 1][xs1si], label="nodata1")
ax.plot(xs[..., 2][xs2si], mynet(Xs).data[..., 2][xs2si], label="nodata2")mydnet = Net(netshape)
mydnet.myinit_with_data(Xs)
mydoptimizer = optim.RMSprop(mydnet.parameters())
mydlosses = []
ax.plot(xs[..., 0][xs0si], mydnet(Xs).data[..., 0][xs0si], label="data0")
ax.plot(xs[..., 1][xs1si], mydnet(Xs).data[..., 1][xs1si], label="data1")
ax.plot(xs[..., 2][xs2si], mydnet(Xs).data[..., 2][xs2si], label="data2")ax.legend()
fig.savefig("exp-3I3O_0.png")# %%
epoches = 1000net.cuda(), mynet.cuda(), mydnet.cuda()
for i in range(epoches):ys = net(Xs_cuda)loss = criterion(ys, Ys_cuda)loss.backward()optimizer.step()myys = mynet(Xs_cuda)myloss = criterion(myys, Ys_cuda)myloss.backward()myoptimizer.step()mydys = mydnet(Xs_cuda)mydloss = criterion(mydys, Ys_cuda)mydloss.backward()mydoptimizer.step()if i % 10 == 0:losses.append(float(loss.data))mylosses.append(float(myloss.data))mydlosses.append(float(mydloss.data))if i % (epoches // 10) == 0:print(losses[-1], mylosses[-1], mydlosses[-1])
net.cpu(), mynet.cpu(), mydnet.cpu()fig, ax = plt.subplots()
fig.set_size_inches(15, 5)
ax.plot(losses[-1500:], label="default")
ax.plot(mylosses[-1500:], label="nodata")
ax.plot(mydlosses[-1500:], label="data")
ax.legend()
fig.savefig("exp-3I3O_2.png")fig, (ax0, ax1, ax2) = plt.subplots(3, 1)
fig.set_size_inches(15, 15)
ax0.scatter(xs, Ys.data, color="pink")
ax1.scatter(xs, Ys.data, color="pink")
ax2.scatter(xs, Ys.data, color="pink")ax0.plot(xs[..., 0][xs0si], net(Xs).data[..., 0][xs0si], label="default0")
ax0.plot(xs[..., 1][xs1si], net(Xs).data[..., 1][xs1si], label="default1")
ax0.plot(xs[..., 2][xs2si], net(Xs).data[..., 2][xs2si], label="default2")
ax0.legend()ax1.plot(xs[..., 0][xs0si], mynet(Xs).data[..., 0][xs0si], label="nodata0")
ax1.plot(xs[..., 1][xs1si], mynet(Xs).data[..., 1][xs1si], label="nodata1")
ax1.plot(xs[..., 2][xs2si], mynet(Xs).data[..., 2][xs2si], label="nodata2")
ax1.legend()ax2.plot(xs[..., 0][xs0si], mydnet(Xs).data[..., 0][xs0si], label="data0")
ax2.plot(xs[..., 1][xs1si], mydnet(Xs).data[..., 1][xs1si], label="data1")
ax2.plot(xs[..., 2][xs2si], mydnet(Xs).data[..., 2][xs2si], label="data2")
ax2.legend()fig.savefig("exp-3I3O_3.png")# %%