1、下载模拟器

这里推荐雷电模拟器 https://www.ldmnq.com/?n=6005

2、在模拟器上安装Autojs

3、连接vscode

1. 打开autojs
2. 打开侧边栏，然后选择连接电脑，打开服务器模式
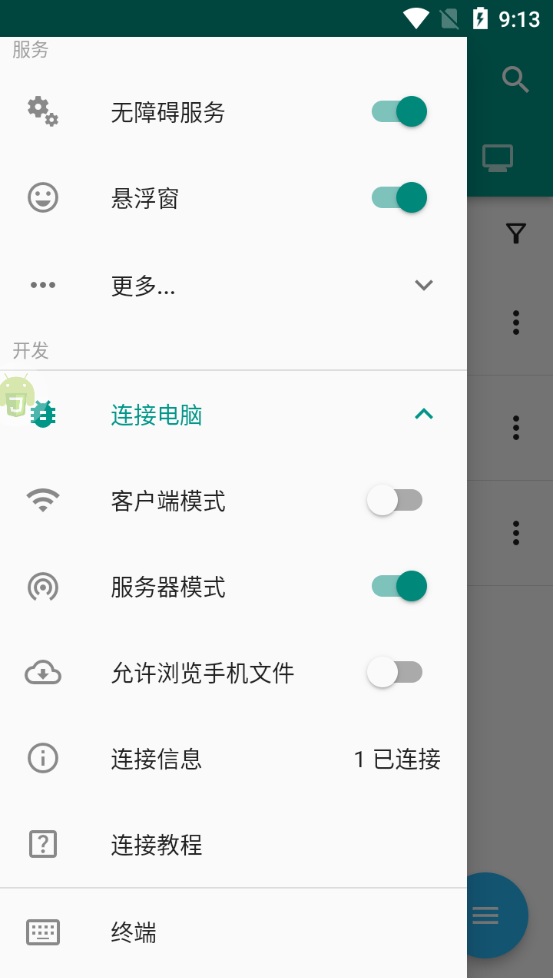
3. 然后复制这个IP地址

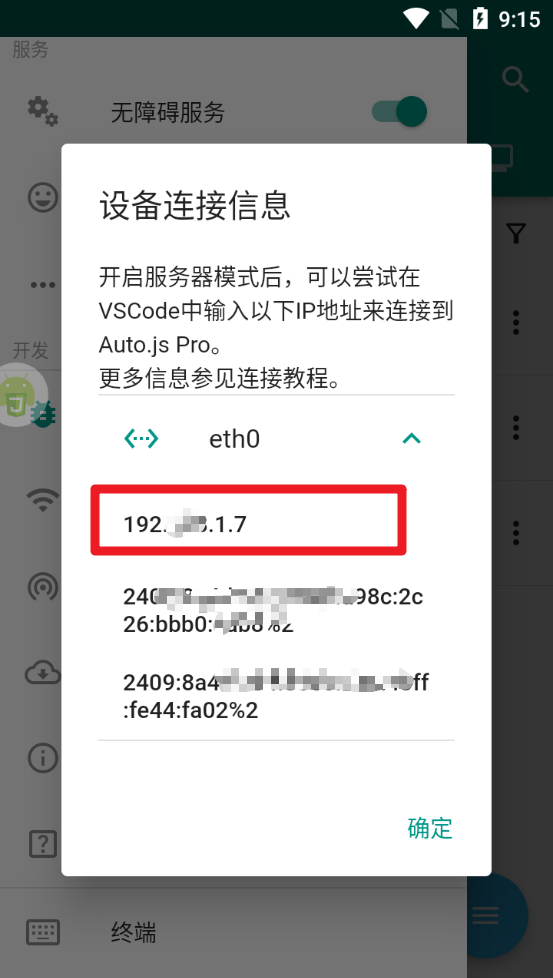
4. 打开vscode
5. 创建一个项目

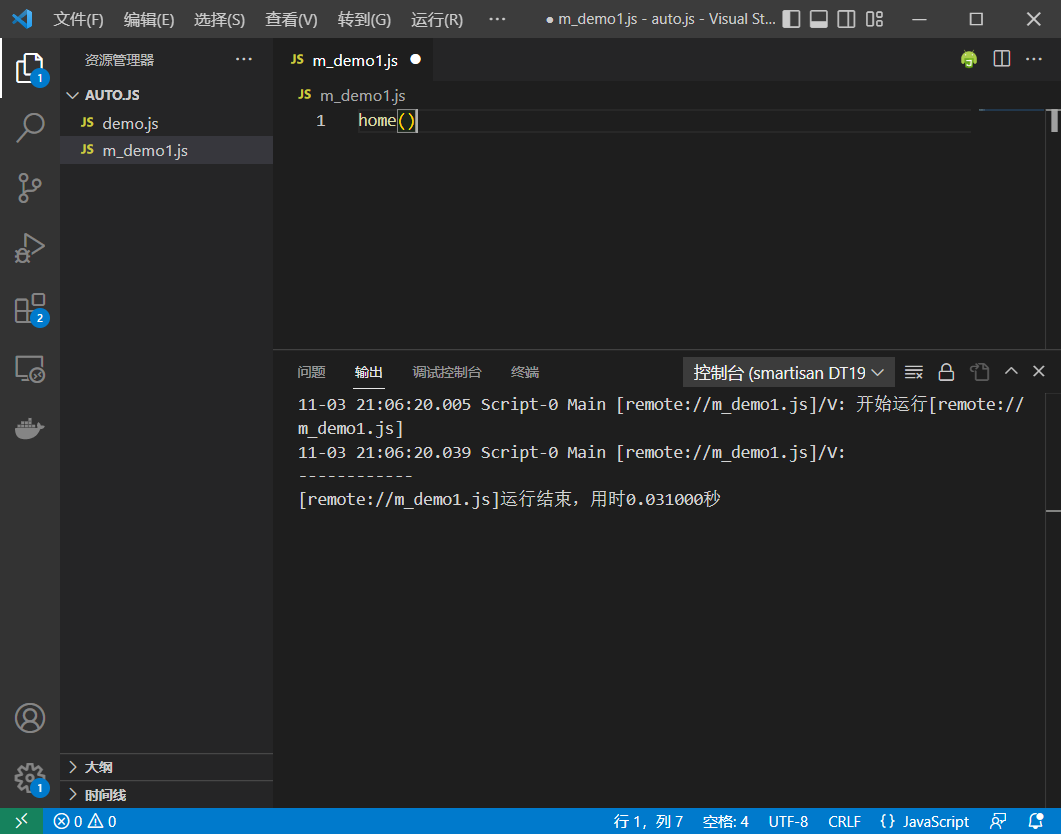
6. 然后摁Ctrl+Shift+P

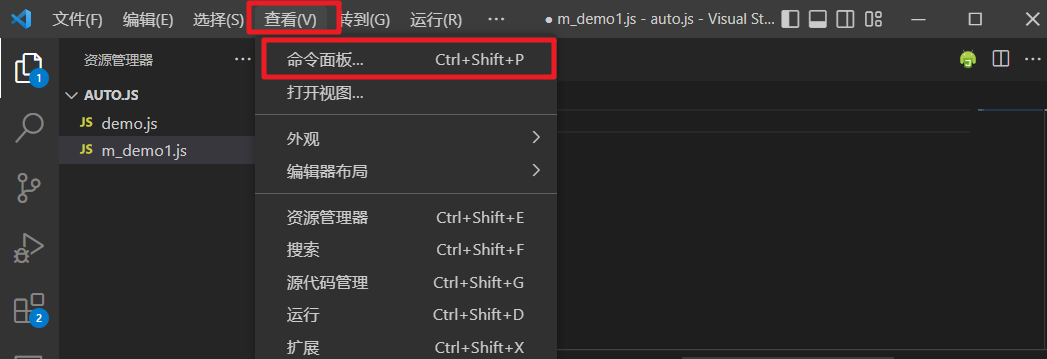
7. 点击（连接到新设备），或者是直接搜索（Auto.js Pro: 连接到新设备）
8. 然后没有的话，要去商店下载插件
9. 下载教程查看这个栏目的第一章https://blog.csdn.net/G_GUi/article/details/126135015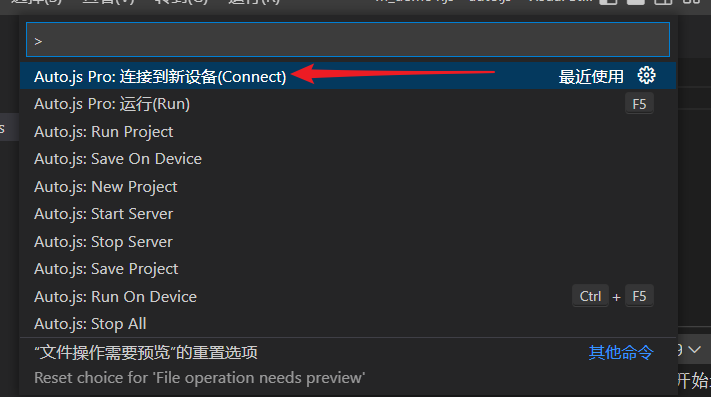
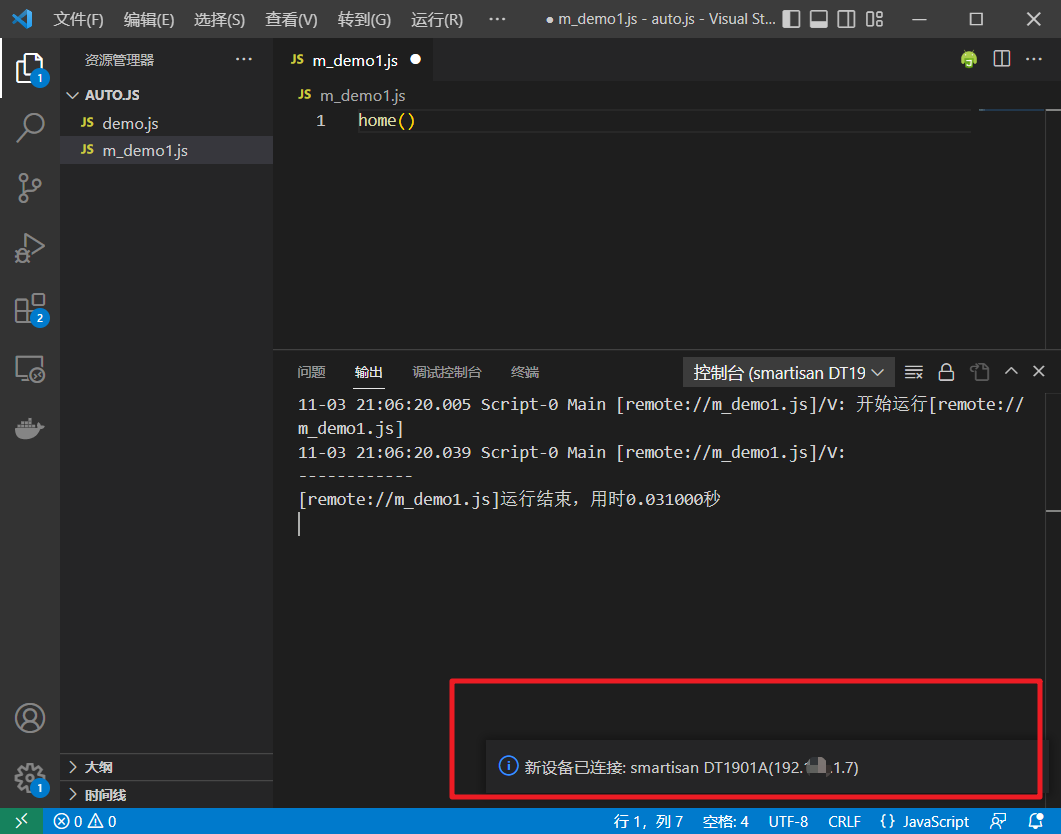
11. 直接输入刚刚的IP地址

连接成功