文章目录
- 一:牛顿法 (Newton's method)
- 1:概述
- 2:牛顿方向与牛顿法
- 3:牛顿法的基本步骤
- 4:举例
- 二:高斯牛顿法 (Gauss–Newton algorithm)
- 1:概述
- 2:高斯牛顿法推导
- 3:高斯牛顿法算法流程
- 4:高斯牛顿法 C++ 代码
- 三:列文伯格-马夸尔特法(Levenberg-Marquardt algorithm)
- 1:概述
- 2:LM算法流程
- 3:列文伯格-马夸尔特法 C++ 代码
- 四:总结
个人笔记:
牛顿(Newton) 法、高斯牛顿(GaussNewton)法、Levenberg-Marquardt(LM)算法等。结合自己需要实现功能的目的,下面主要给出推导结果、代码实现和实际一些应用。推导过程最后会放一些个人参考的一些文章和资料。
一:牛顿法 (Newton’s method)
1:概述
牛顿法是一种函数逼近法,它的基本思想是:在极小点附近用x(k)x^{(k)}x(k)点的二阶泰勒多项式来近似目标函数f(x)f(x)f(x),并用选代点x(k)x^{(k)}x(k)处指向近似二次函数的极小点方向作为搜索方向p(k)p^{(k)}p(k)。
设规划问题 :minf(x),x∈Rnmin f(x),x∈R^nminf(x),x∈Rn
其中f(x)f(x)f(x)在点x(k)x^{(k)}x(k)处具有二阶连续偏导数,黑森矩阵▽2f(x(k))▽^2f(x^{(k)})▽2f(x(k))正定。
现已有f(x)f(x)f(x)极小点的第kkk级估计值x(k)x^{(k)}x(k),并将f(x)f(x)f(x)作二阶泰勒展开:
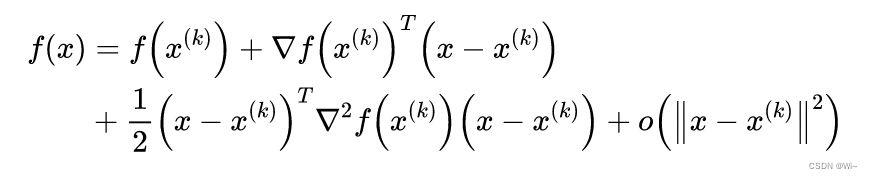 其中主要的是前三项,最后一项为高阶无穷小。
其中主要的是前三项,最后一项为高阶无穷小。
2:牛顿方向与牛顿法
记上式中的主要部分为:
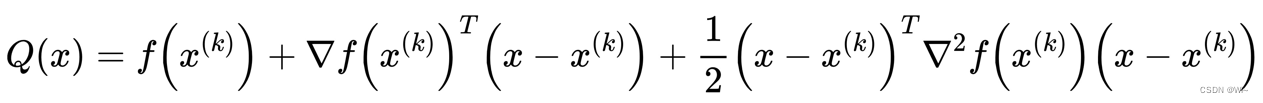
在x(k)x^{(k)}x(k)附近可用Q(x)Q(x)Q(x)来近似f(x)f(x)f(x), Q(x)≈f(x)Q(x) ≈ f(x)Q(x)≈f(x)。
故可以用Q(x)Q(x)Q(x)的极小点来近似f(x)f(x)f(x)的极小点,求Q(x)Q(x)Q(x)的驻点:
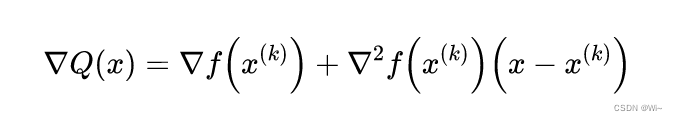
由梯度▽Q(x)=0▽Q(x) = 0▽Q(x)=0得Q(x)Q(x)Q(x)的平稳点x(k+1)x^{(k+1)}x(k+1),p(k)p^{(k)}p(k)是牛顿方向,步长为111
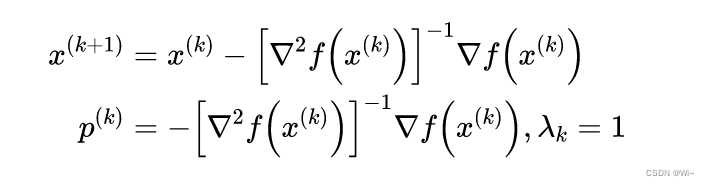
也就是下面描述,其中HHH是黑塞矩阵
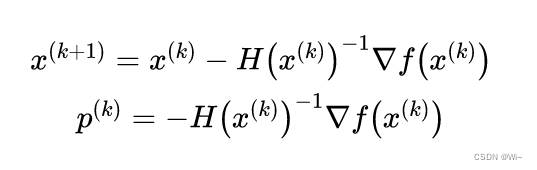
3:牛顿法的基本步骤
1:选取初始数据:初始点x(0)x^{(0)}x(0),终止条件ε>0ε>0ε>0,令k:=0k:=0k:=0
2:求梯度向量▽f(k)▽f^{(k)}▽f(k),并计算∣∣▽f(k)∣∣||▽f^{(k)}||∣∣▽f(k)∣∣:
若∣∣▽f(k)∣∣<ε||▽f^{(k)}||<ε∣∣▽f(k)∣∣<ε,停止选代,输出x(k)x^{(k)}x(k),否则转下一步。
3:构造牛顿方向:
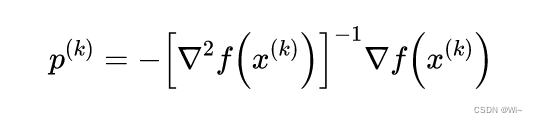
4:算法迭代:
计算x(k+1)=x(k)+p(k)x^{(k+1)} = x^{(k)} + p^{(k)}x(k+1)=x(k)+p(k),以x(k+1)x^{(k+1)}x(k+1)作为下一轮迭代点,令k:=k+1k := k+1k:=k+1,转第2步。
4:举例
试用牛顿法求函数f(x)=x12+25x22f(x) = x_1^2 + 25x_2^2f(x)=x12+25x22 的极小点,其中初始点为x(0)=(2,2)Tx^{(0)} = (2, 2)^Tx(0)=(2,2)T, ε=10−6ε = 10^{-6}ε=10−6.
解(1)求梯度和黑塞矩阵:
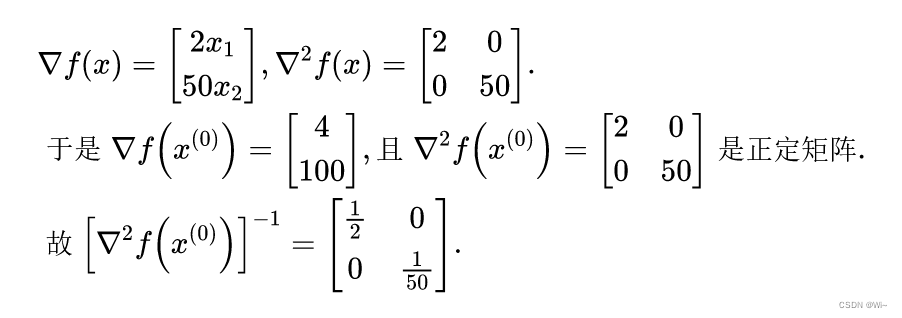
(2)确定牛顿方向:
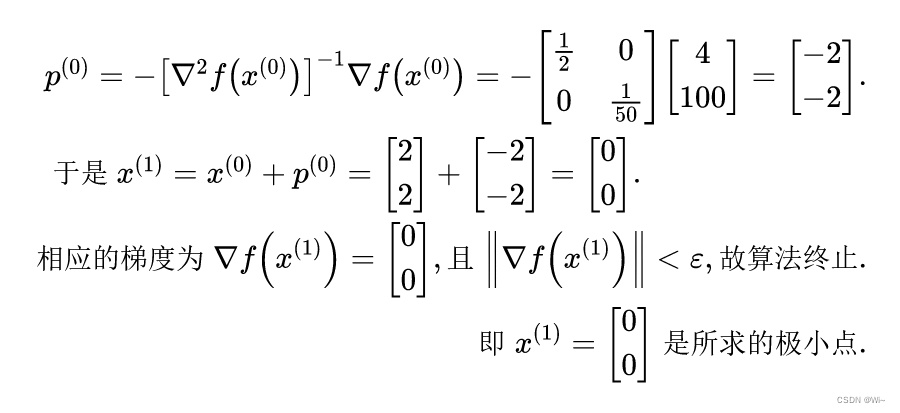 即:x1=0,x2=0x_1 = 0,x_2=0x1=0,x2=0
即:x1=0,x2=0x_1 = 0,x_2=0x1=0,x2=0
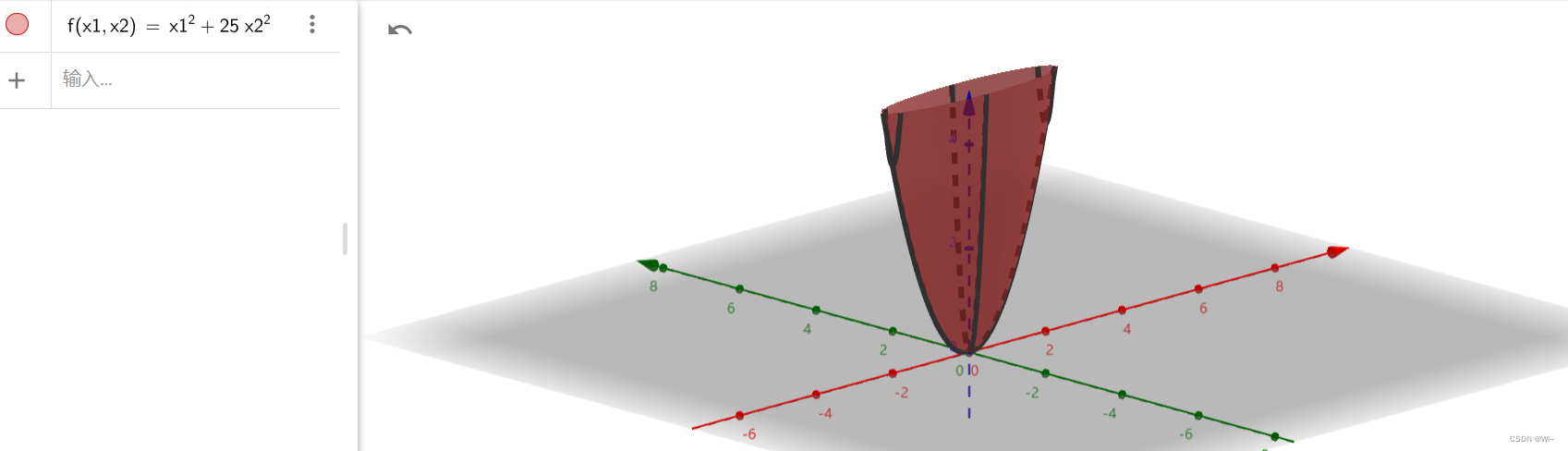
这里使用三维坐标系来查看x1=0,x2=0x_1 = 0,x_2=0x1=0,x2=0存在极值
二:高斯牛顿法 (Gauss–Newton algorithm)
1:概述
高斯-牛顿算法用于求解非线性最小二乘问题,相当于最小化函数值的平方和。它是牛顿求非线性函数最小值方法的扩展。由于平方和必须是非负的,因此该算法可以看作是使用牛顿法迭代地逼近和的零点,从而使和最小化。它的优点是不需要计算可能具有挑战性的二阶导数(也就是黑塞矩阵)。
这里说一下,牛顿法使用黑塞矩阵有个缺点:计算量特别大。高斯牛顿法是在牛顿法的基础上用雅可比矩阵代替了黑森矩阵。
注意:高斯牛顿法针对非线性最小二乘问题。最小二乘详解
2:高斯牛顿法推导
①:目标函数问题:自变量xxx 经过模型函数得出因变量yyy,mmm个观测点:
X=[x1,x2,...xm]TX=[x_1,x_2,...x_m]^TX=[x1,x2,...xm]T,Y=[y1,y2,...ym]TY=[y_1,y_2,...y_m]^TY=[y1,y2,...ym]T
②:模型函数:Y=f(X;β1,β2,...,βn)Y = f(X;β_1,β_2,...,β_n)Y=f(X;β1,β2,...,βn) => f(x;β)f(x;β)f(x;β)
其中 xxx 是自变量 ,yyy 是因变量,βββ 是目标参数。x和yx和yx和y是已知的,优化 βββ 目标参数。
③:优化目标函数:minS=∑i=1n(f(xi;β)−yi)2min S = \displaystyle\sum_{i=1}^{n}(f(x_i;β)-y_i)^2minS=i=1∑n(f(xi;β)−yi)2
④:第 iii 次观测点的预测偏差:ri=f(xi;β)−yi)2r_i = f(x_i;β)-y_i)^2ri=f(xi;β)−yi)2,那么每次的偏差组成一个向量形式:R=[r1,r2,...rm]TR = [r_1,r_2,...r_m]^TR=[r1,r2,...rm]T
⑤:对于③目标函数 可以写成:minS=∑i=1nri2=RTRmin S = \displaystyle\sum_{i=1}^{n}r_i^2 = R^TRminS=i=1∑nri2=RTR
⑥:那么目标函数梯度:▽S(β)=[∂S∂β1,∂S∂β2,...,∂S∂βn]T▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T,其中对每个参数 βjβ_jβj 求偏导∂S∂βj=2∑i=1mri∂ri∂βj\frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j}∂βj∂S=2i=1∑mri∂βj∂ri
⑦:对于R=[r1,r2,...rm]T和βR = [r_1,r_2,...r_m]^T和βR=[r1,r2,...rm]T和β的偏导形式就可以写成 雅可比矩阵
J(R(β))=[∂r1∂β1...∂r1∂βn⋮⋱⋮∂rm∂β1...∂rm∂βn]J(R(β)) = \begin{bmatrix} \frac{\partial r_1}{\partial β_1}&...&\frac{\partial r_1}{\partial β_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_m}{\partial β_1}&...&\frac{\partial r_m}{\partial β_n}\end{bmatrix}J(R(β))=⎣⎢⎡∂β1∂r1⋮∂β1∂rm...⋱...∂βn∂r1⋮∂βn∂rm⎦⎥⎤
⑧:目标函数梯度(一阶偏导):▽S(β)=[∂S∂β1,∂S∂β2,...,∂S∂βn]T=>∂S∂βj=2∑i=1mri∂ri∂βj=>▽S=2JTR▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T => \frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j} => ▽S = 2J^TR▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T=>∂βj∂S=2i=1∑mri∂βj∂ri=>▽S=2JTR
⑨:求目标函数黑塞矩阵(二阶偏导):
由梯度向量元素 ∂S∂βj=2∑i=1mri∂ri∂βj\frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j}∂βj∂S=2i=1∑mri∂βj∂ri 到黑塞矩阵元素∂2S∂βk∂βj=2∂∂βk(∑i=1mri∂ri∂βj)\frac{\partial ^2S}{\partial β_k\partial β_j} = 2\frac{\partial }{\partial β_k} (\displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j})∂βk∂βj∂2S=2∂βk∂(i=1∑mri∂βj∂ri),
应用链式法则得:∂2S∂βk∂βj=2∑i=1m(∂ri∂βk∂ri∂βj+ri∂2ri∂βk∂βj)\frac{\partial ^2S}{\partial β_k\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}(\frac{\partial r_i}{\partial β_k}\frac{\partial r_i}{\partial β_j} + r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j})∂βk∂βj∂2S=2i=1∑m(∂βk∂ri∂βj∂ri+ri∂βk∂βj∂2ri),
其中OOO矩阵元素 :Okj=∑i=1mri∂2ri∂βk∂βjO_{kj} = \displaystyle\sum_{i=1}^{m}r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j}Okj=i=1∑mri∂βk∂βj∂2ri
黑塞矩阵:H=2(JTJ+O)H = 2(J^TJ + O)H=2(JTJ+O)
⑩:写成牛顿法形式:如果模型比较好,其中OOO矩阵rir_iri是趋近于0的。这里就把OOO矩阵忽略掉,方便计算。
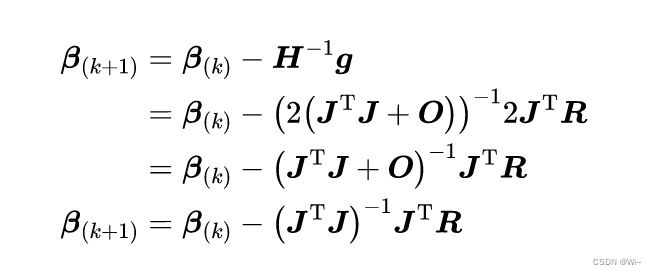
3:高斯牛顿法算法流程
1:给定初始参数值 β0β_0β0 (默认是为 111 的向量)。设ε=1−10ε = 1^{-10}ε=1−10
2:对于第 kkk 次选代,求出当前的雅可比矩阵 J(βk)J(β_k)J(βk) 和残差值 f(βk)f(β_k)f(βk)也就是RRR。
3:求解增量方程: HΔβk=−gH\Delta β_k = -gHΔβk=−g
=> Δβk=−H−1g\Delta β_k= -H^{-1}gΔβk=−H−1g
=> Δβk≈−(JTJ)−1JTR\Delta β_k≈ -(J^TJ)^{-1}J^TRΔβk≈−(JTJ)−1JTR 。这里用雅可比矩阵 JTJJ^TJJTJ 近似黑塞矩阵HHH。
4:若 Δβk<ε\Delta β_k<εΔβk<ε ,则停止。否则,令βk+1=βk+Δβkβ_{k+1} = β_k +\Delta β_kβk+1=βk+Δβk,返回第2步。
4:高斯牛顿法 C++ 代码
//求雅克比矩阵template <class FunctionPredictedValue>MatrixXd Jacobi(const VectorXd& inVectorValue, const VectorXd& params,FunctionPredictedValue funPV){int rowNum = inVectorValue.rows();int colNum = params.rows();MatrixXd Jac(rowNum, colNum);for (int i = 0; i < rowNum; i++){for (int j = 0; j < colNum; j++){Jac(i, j) = Deriv(inVectorValue, i, params, j,funPV);}}return Jac;}//残差值向量template <class FunctionPredictedValue>ArrayXd ResidualsVector(const VectorXd& inVectorValue, const VectorXd& outVectorValue,const VectorXd& params,FunctionPredictedValue funPV){int dataCount = inVectorValue.rows();//保存残差值ArrayXd residual(dataCount);//获取预测偏差值 r= ^y(预测值) - y(实际值)for(int i=0;i<dataCount;++i){//获取预测值double predictedValue = funPV(inVectorValue(i),params);residual(i) = predictedValue - outVectorValue(i);}return residual;}//求导template <class FunctionPredictedValue>double Deriv(const VectorXd& inVectorValue, int objIndex, const VectorXd& params,int paraIndex,FunctionPredictedValue funPV){VectorXd para1 = params;VectorXd para2 = params;para1(paraIndex) -= DERIV_STEP;para2(paraIndex) += DERIV_STEP;double obj1 = funPV(inVectorValue(objIndex), para1);double obj2 = funPV(inVectorValue(objIndex), para2);return (obj2 - obj1) / (2 * DERIV_STEP);}/* 高斯牛顿法(GNA) 解决非线性最小二乘问题 确定目标函数和约束来对现有的参数优化*/template <class FunctionPredictedValue>ArrayXd GaussNewtonAlgorithm(const ArrayXd & inVectorValue,const ArrayXd & outVectorValue,ArrayXd params,FunctionPredictedValue funPV,int maxIteCount = 1,double epsilon = 1e-10){int k=0;//数据个数int dataCount = inVectorValue.size();// ε 终止条件//double epsilon = 1e-10;//残差值ArrayXd residual(dataCount);//found 为true 结束循环bool found = false;while(!found && k<maxIteCount){//迭代增加k++;//获取预测偏差值 r= ^y(预测值) - y(实际值)residual = ResidualsVector( inVectorValue, outVectorValue,params, funPV);//求雅克比矩阵MatrixXd Jac = Jacobi(inVectorValue,params,funPV);// Δx = - (Jac^T * Jac)^-1 * Jac^T * rArrayXd delta_x = - (((Jac .transpose() * Jac ).inverse()) * Jac.transpose() * residual.matrix()).array();qDebug()<<QString("高斯牛顿法:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(delta_x.abs().sum());//达到精度,结束if(delta_x.abs().sum() < epsilon){found = true;}//x(k+1) = x(k) + Δxparams = params + delta_x;}return params;}
Matrix是Eigen库中的一个矩阵类,这里引入Eigen库方便代数运算。
三:列文伯格-马夸尔特法(Levenberg-Marquardt algorithm)
1:概述
在数学和计算中,Levenberg–Marquardt 算法(LMA或简称LM),也称为 阻尼最小二乘法( DLS ),用于解决非线性最小二乘法问题。这些最小化问题尤其出现在最小二乘 曲线拟合中。LMA 在高斯-牛顿算法(GNA) 和梯度下降法之间进行插值。LMA 更稳健比 GNA,这意味着在许多情况下,即使它开始时离最终最小值很远,它也能找到解决方案。对于性能良好的函数和合理的启动参数,LMA 往往比 GNA 慢。LMA 也可以被视为使用信赖域方法的高斯-牛顿。
LMA 在许多软件应用程序中用于解决一般曲线拟合问题。通过使用高斯-牛顿算法,它通常比一阶方法收敛得更快。然而,与其他迭代优化算法一样,LMA 只能找到局部最小值,不一定是全局最小值。与其他数值最小化算法一样,Levenberg–Marquardt 算法是一个迭代过程。要开始最小化,用户必须提供参数向量的初始猜测 βββ, 在只有一个最小值的情况下,一个不知情的标准猜测就像β=[1,1,...,1]Tβ = [1,1,...,1]^Tβ=[1,1,...,1]T会工作得很好;在有多个最小值的情况下,只有当初始猜测已经有点接近最终解决方案时,算法才会收敛到全局最小值。
2:LM算法流程
1:给定初始参数值 β0β_0β0 (默认是为 111 的向量)。初始μ0μ_0μ0的选择可以依赖于H0=J(β0)TJ(β0)H_0=J(β_0)^TJ(β_0)H0=J(β0)TJ(β0) 中的元素,一般我们选择 μ0=τ∗maxi{Hii(0)}μ_0 =τ*max_i\{H_{ii}^{(0)}\}μ0=τ∗maxi{Hii(0)},一般τ=10−6τ=10^{−6}τ=10−6,这里设置ε1=1−10ε_1 = 1^{-10}ε1=1−10和ε2=1−10ε_2 = 1^{-10}ε2=1−10。
2:若∣∣g∣∣∞≤ε1||g||_\infty≤ε_1∣∣g∣∣∞≤ε1 成立,则停止。
3:对于第 kkk 次选代,求出当前的雅可比矩阵 J(βk)J(β_k)J(βk) 和残差值 f(βk)f(β_k)f(βk)也就是RRR。
4:求解增量方程: (H+μkI)Δβk=−g(H+μ_kI)\Delta β_k = -g(H+μkI)Δβk=−g
=> Δβk=−(H+μkI)−1g\Delta β_k= -(H+μ_kI)^{-1}gΔβk=−(H+μkI)−1g
=> Δβk≈−(JTJ+μkI)−1JTR\Delta β_k≈ -(J^TJ+μ_kI)^{-1}J^TRΔβk≈−(JTJ+μkI)−1JTR 。这里用雅可比矩阵 JTJJ^TJJTJ 近似黑塞矩阵HHH。
5:若 ∣∣Δβk∣∣≤ε2(∣∣βk∣∣+ε2)||\Delta β_k||≤ε_2(||β_k|| + ε_2)∣∣Δβk∣∣≤ε2(∣∣βk∣∣+ε2) 成立,则停止。否则,令βk+1=βk+Δβkβ_{k+1} = β_k +\Delta β_kβk+1=βk+Δβk。
6:ρ=∣∣F(βk)∣∣22−∣∣F(βk+Δβk)∣∣22L(0)−L(Δβk)\rho = \frac{||F(β_k)||_2^2-||F(β_k+\Delta β_k)||_2^2}{L(0) - L(\Delta β_k)}ρ=L(0)−L(Δβk)∣∣F(βk)∣∣22−∣∣F(βk+Δβk)∣∣22,如果ρ>0\rho >0ρ>0,求出当前的黑塞矩阵 H≈J(βk)TJ(βk)H ≈ J(β_k)^TJ(β_k)H≈J(βk)TJ(βk) 和梯度 g=J(βk)Tf(βk)g = J(β_k)^Tf(β_k)g=J(βk)Tf(βk)。若∣∣g∣∣∞≤ε1||g||_\infty≤ε_1∣∣g∣∣∞≤ε1 成立,则停止。更新 μkμ_kμk,μk=μk∗max{13,1−(2ρ−1)3};v=2μ_k =μ_k*max\{\frac{1}{3},1-(2\rho-1)^3\};v=2μk=μk∗max{31,1−(2ρ−1)3};v=2。如果ρ≤0\rho ≤0ρ≤0,μk=μk∗v;v=2∗vμ_k =μ_k*v; v=2*vμk=μk∗v;v=2∗v。
最终伪代码如下:

3:列文伯格-马夸尔特法 C++ 代码
/* 列文伯格马夸尔特法(LMA) == 使用信赖域的高斯牛顿法,鲁棒性更好, 确定目标函数和约束来对现有的参数优化*/template <class FunctionPredictedValue>ArrayXd LevenbergMarquardtAlgorithm(const ArrayXd &inVectorValue,const ArrayXd & outVectorValue, ArrayXd params,FunctionPredictedValue funPV,int maxIteCount = 1,double epsilon = 1e-10){//数据个数int dataCount = inVectorValue.size();// ε 终止条件//double epsilon = 1e-10;// τdouble tau = 1e-6;//迭代次数int k=0;int v=2;//求雅可比矩阵MatrixXd Jac = Jacobi(inVectorValue,params,funPV);//用雅可比矩阵近似黑森矩阵MatrixXd Hessen = Jac .transpose() * Jac ;//获取预测偏差值 r= ^y(预测值) - y(实际值)//保存残差值ArrayXd residual = ResidualsVector(inVectorValue, outVectorValue,params,funPV);//梯度MatrixXd g = Jac.transpose() * residual.matrix();//found 为true 结束循环bool found = ( g.lpNorm<Eigen::Infinity>() <= epsilon );//阻尼参数μdouble mu = tau * Hessen.diagonal().maxCoeff();while(!found && k<maxIteCount){k++;//LM方向 uI => I 用黑森矩阵对角线代替//MatrixXd delta_x = - (Hessen + mu*Hessen.asDiagonal().diagonal()).inverse() * g;MatrixXd delta_x = - (Hessen + mu*MatrixXd::Identity(Hessen.cols(), Hessen.cols())).inverse() * g;if( delta_x.lpNorm<2>() <= epsilon * (params.matrix().lpNorm<2>() + epsilon )){qDebug()<<QString("LM:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(delta_x.lpNorm<2>());found = true;}else{MatrixXd newParams = params + delta_x.array();//保存残差值ArrayXd residualOld(dataCount),residualNew(dataCount);//获取预测偏差值 r= ^y(预测值) - y(实际值) 旧值residualOld = ResidualsVector( inVectorValue, outVectorValue,params, funPV);//获取预测偏差值 r= ^y(预测值) - y(实际值) 新值residualNew = ResidualsVector( inVectorValue, outVectorValue,newParams, funPV);//ρ (-(delta_x.transpose()*g) - 0.5*(delta_x.transpose() * Hessen * delta_x)).sum();double rho = (residualOld.pow(2).sum() - residualNew.pow(2).sum()) / (0.5*delta_x.transpose()*(mu * delta_x - g)).sum() ;if(rho>0){params = newParams;Jac = Jacobi(inVectorValue,params,funPV);Hessen = Jac.transpose() * Jac ;//获取预测偏差值 r= ^y(预测值) - y(实际值)residual = ResidualsVector( inVectorValue, outVectorValue,params, funPV);g = Jac.transpose() * residual.matrix();found = ( g.lpNorm<Eigen::Infinity>() <= epsilon );qDebug()<<QString("LM:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(g.lpNorm<Eigen::Infinity>());mu = mu* qMax(1/3.0 , 1-qPow(2*rho -1,3));v=2;}else{mu = mu*v;v = 2*v;}}}return params;}//FunctionPredictedValue 是一个自定义函数,可以定义自己的函数 规则
//设置规则,获取预测值 ==》自变量和参数
//曲线拟合函数
class CurveFittingFunction
{
public:double operator()(const double &inValue ,const ArrayXd ¶ms){double value=0;int paramsCount = params.rows();for(int i=0;i<paramsCount;++i){//这里使用曲线方程 y = a1*x^0 + a2*x^1 + a3*x^2 + ... 根据参数(a1,a2,a3,...)个数来设置value += params(i) * qPow(inValue,i);}return value;}
};四:总结
1:工具:主要Qt + Eigen库 + QCustomPlot类
Eigen库是一个用于矩阵计算,代数计算库
QCustomPlot类是一个用于绘图和数据可视化
2:上面完整代码已上传GitHub
3:参考文献
黑塞矩阵和雅可比矩阵理解
高斯牛顿法详解
LM算法详解
LM论文



![[附源码]计算机毕业设计springboot餐馆点餐管理系统](https://img-blog.csdnimg.cn/680a81d53114401cb1710cd74fd42c62.png)
![[附源码]计算机毕业设计springboot房屋租赁系统](https://img-blog.csdnimg.cn/31f1ef3b9dd947d7b8d47829bbcd6460.png)