DFIG控制10: 双馈发电机的动态模型。主要介绍DFIG在三相坐标系、定子αβ坐标系、dq同步坐标系下的模型。
本文主要是整理了DFIG的动态模型的公式和坐标变换的过程。某些描述是为了便于自己理解,不一定准确。
大部分内容参考:
G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.
模型主要包括4个方程:电压、磁链、转矩、运动。
三相坐标系模型
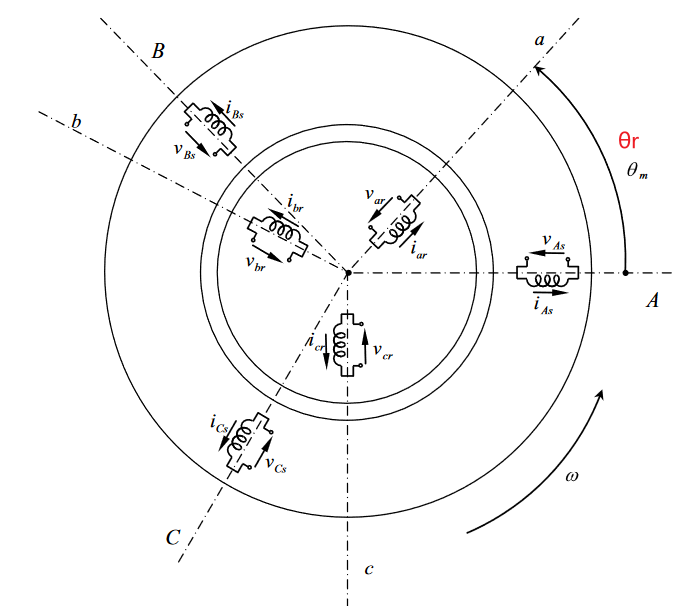
示意图
示意图如下,ABC定子,里面的转子abc在旋转。转子的各个参数已经折算到定子侧,折算后定子和转子的匝数相同。(折算方式类似于变压器的原副边折算)。转子的三个绕组旋转的角速度为转子的电角速度θr\theta_rθr,是机械角速度乘以极对数npθmn_p\theta_mnpθm
电压方程
对于定子:
uA,B,C=RsiA,B,C+dψA,B,Cdtu_{A,B,C}=R_si_{A,B,C}+\frac{d\psi_{A,B,C}}{dt} uA,B,C=RsiA,B,C+dtdψA,B,C
其实就是电压和磁链的关系(电磁感应定律),并且考虑了绕组内阻上的压降 。
或者写成矩阵形式:
[uAuBuC]=[Rs000Rs000Rs][iAiBiC]+ddt[ψAψBψC]\left[\begin{matrix} u_A \\ u_B \\ u_C \end{matrix}\right] = \left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right] \left[\begin{matrix} i_A \\ i_B \\ i_C \end{matrix}\right] + \frac{d}{dt}\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \end{matrix}\right] uAuBuC=Rs000Rs000RsiAiBiC+dtdψAψBψC
RsR_sRs为定子绕组的内阻。
对于转子,
ua,b,c=Rria,b,c+dψa,b,cdtu_{a,b,c}=R_ri_{a,b,c}+\frac{d\psi_{a,b,c}}{dt} ua,b,c=Rria,b,c+dtdψa,b,c
RsR_sRs为转子绕组的内阻。
或者写成矩阵形式:
[uaubuc]=[Rr000Rr000Rr][iaicic]+ddt[ψaψbψc]\left[\begin{matrix} u_a \\ u_b \\ u_c \end{matrix}\right] = \left[\begin{matrix} R_r & 0 & 0 \\ 0 & R_r & 0 \\ 0 & 0 & R_r \end{matrix}\right] \left[\begin{matrix} i_a \\ i_c \\ i_c \end{matrix}\right] + \frac{d}{dt}\left[\begin{matrix} \psi_a \\ \psi_b \\ \psi_c \end{matrix}\right] uaubuc=Rr000Rr000Rriaicic+dtdψaψbψc
磁链方程
这部分内容还是可以参考变压器的模型。看了这个视频,觉得讲得还挺清楚的:第十一讲 风力发电系统基本结构+双馈电机数学模型第一部分_哔哩哔哩_bilibili
把DFIG的3个定子绕组相当于3个位置固定的电感(星形连接的),而3个转子绕组相当于3个旋转的电感(也是星形连接的)。这些电感的部分磁链于其他电感有交链,也有部分只在绕组自身交链(类似变压器的漏感)。
考虑所有这些交链关系(ψ=∑Lxix\psi=\sum L_xi_xψ=∑Lxix),定子和转子的磁链为:
[ψAψBψCψaψbψc]=[LAALABLACLAaLAbLAcLBALBBLBCLBaLBbLBcLCALCBLCCLCaLCbLCcLaALaBLaCLaaLabLacLbALbBLbCLbaLbbLbcLcALcBLcCLcaLcbLcc][iAiBiCiaibic]\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \\ \psi_a \\ \psi_b \\ \psi_c \end{matrix}\right] = \left[\begin{matrix} L_{AA} & L_{AB} & L_{AC} & L_{Aa} & L_{Ab} & L_{Ac}\\ L_{BA} & L_{BB} & L_{BC} & L_{Ba} & L_{Bb} & L_{Bc} \\ L_{CA} & L_{CB} & L_{CC} & L_{Ca} & L_{Cb} & L_{Cc} \\ L_{aA} & L_{aB} & L_{aC} & L_{aa} & L_{ab} & L_{ac}\\ L_{bA} & L_{bB} & L_{bC} & L_{ba} & L_{bb} & L_{bc} \\ L_{cA} & L_{cB} & L_{cC} & L_{ca} & L_{cb} & L_{cc} \\ \end{matrix}\right] \left[\begin{matrix} i_A \\ i_B \\ i_C \\ i_a \\ i_b \\ i_c \end{matrix}\right] ψAψBψCψaψbψc=LAALBALCALaALbALcALABLBBLCBLaBLbBLcBLACLBCLCCLaCLbCLcCLAaLBaLCaLaaLbaLcaLAbLBbLCbLabLbbLcbLAcLBcLCcLacLbcLcciAiBiCiaibic
其中,定子-定子之间以及转子-转子之间的电感,由于相对位置是固定的,所以电感值是常数。而定子-转子之间的电感,由于转子在转动,电感值随转子的电角度θr\theta_rθr变化。
所以可以分成4部分:
[ψsψr]=[LssLsr(θr)Lrs(θr)Lrr][isir]\left[\begin{matrix} \boldsymbol{\psi}_s \\ \boldsymbol{\psi}_r \end{matrix}\right] = \left[\begin{matrix} \boldsymbol{L}_{ss} & \boldsymbol{L}_{sr}(\theta_r) \\ \boldsymbol{L}_{rs}(\theta_r) & \boldsymbol{L}_{rr} \end{matrix}\right] \left[\begin{matrix} \boldsymbol{i}_s \\ \boldsymbol{i}_r \end{matrix}\right] [ψsψr]=[LssLrs(θr)Lsr(θr)Lrr][isir]
下标s表示定子的3个变量,下标r表示转子的3个变量。6x6的电感矩阵,按照系数是否随电角度变化,分成了4个3x3的矩阵。
再来看一下这4个矩阵。
定子:
Lss=[Lm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls]\boldsymbol{L}_{ss}= \left[\begin{matrix} L_{m}+L_{ls} & -0.5L_m & -0.5L_m \\ -0.5L_m & L_{m}+L_{ls} & -0.5L_m \\ -0.5L_m & -0.5L_m & L_{m}+L_{ls} \end{matrix}\right]Lss=Lm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls−0.5Lm−0.5Lm−0.5LmLm+Lls
LmL_mLm是磁链有交链的部分,由于三相绕组120°的位置关系,其他两相绕组对另一相的互感都是Lmcos120∘=−0.5LmL_m cos120^\circ=-0.5L_mLmcos120∘=−0.5Lm,没有交链的是定子每相的漏感LlsL_{ls}Lls。
转子侧公式类似:
Lrr=[Lm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr]\boldsymbol{L}_{rr}= \left[\begin{matrix} L_{m}+L_{lr} & -0.5L_m & -0.5L_m \\ -0.5L_m & L_{m}+L_{lr} & -0.5L_m \\ -0.5L_m & -0.5L_m & L_{m}+L_{lr} \end{matrix}\right]Lrr=Lm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr−0.5Lm−0.5Lm−0.5LmLm+Llr
注意因为做了折算,交链的部分和定子一样,为LmL_mLm。不同的是,转子每相的漏感为LlrL_{lr}Llr。
定子转子之间:
Lsr(θr)=Lrs(θr)T=[LAaLAbLAcLBaLBbLBcLCaLCbLCc]=Lm[cos(θr)cos(θr+120∘)cos(θr−120∘)cos(θr−120∘)cos(θr)cos(θr+120∘)cos(θr+120∘)cos(θr−120∘)cos(θr)]\begin{align*} &\boldsymbol{L}_{sr}(\theta_r)=\boldsymbol{L}_{rs}(\theta_r)^T = \left[\begin{matrix} L_{Aa} & L_{Ab} & L_{Ac}\\ L_{Ba} & L_{Bb} & L_{Bc} \\ L_{Ca} & L_{Cb} & L_{Cc} \\ \end{matrix}\right]\\ &=L_m\left[\begin{matrix} cos(\theta_r) & cos(\theta_r+120^\circ) & cos(\theta_r-120^\circ) \\ cos(\theta_r-120^\circ) & cos(\theta_r) & cos(\theta_r+120^\circ) \\ cos(\theta_r+120^\circ) & cos(\theta_r-120^\circ) & cos(\theta_r) \end{matrix}\right]\end{align*} Lsr(θr)=Lrs(θr)T=LAaLBaLCaLAbLBbLCbLAcLBcLCc=Lmcos(θr)cos(θr−120∘)cos(θr+120∘)cos(θr+120∘)cos(θr)cos(θr−120∘)cos(θr−120∘)cos(θr+120∘)cos(θr)
看第一行:当转子的a相和定子的A相重合时,θr=0\theta_r=0θr=0,此时互感LAaL_{Aa}LAa达到最大值LmL_mLm。此时转子b相的物理位置超前a相120°,c相超前240°(相当于滞后120°),所以有这样的表达式。先了解到这里,没继续看更细节的内容。(这里简单认为极对数=1)
转矩和运动方程
这个没仔细看,只记录一下公式,后面转矩方程需要和电压、磁链方程一起做坐标变换。(发现篇幅太长了,转矩部分还是下次再写)。
转矩方程:
Te=npLm[(iAia+iBib+iCic)sinθr+(iAib+iBic+iCia)sin(θr+120∘)+(iAic+iBia+iCib)sin(θr−120∘)]\begin{align*} T_e=& n_pL_m[(i_Ai_a+i_Bi_b+i_Ci_c)sin\theta_r+\\ & (i_Ai_b+i_Bi_c+i_Ci_a)sin(\theta_r+120^\circ)+ \\ & (i_Ai_c+i_Bi_a+i_Ci_b )sin(\theta_r-120^\circ)] \end{align*} Te=npLm[(iAia+iBib+iCic)sinθr+(iAib+iBic+iCia)sin(θr+120∘)+(iAic+iBia+iCib)sin(θr−120∘)]
理想的运动方程(应该是大物里面见过):
Jnpdωrdt=Te−TL\frac{J}{n_p}\frac{d\omega_r}{dt}=T_e-T_L npJdtdωr=Te−TL
描述了电机在电磁转矩TeT_eTe和负载转矩TLT_LTL作用下的加减速。ωr/np\omega_r/n_pωr/np为机械角速度,J为转动惯量。
定子αβ静止坐标系模型
为了简化模型,引入了3/2变换(Clarke变换)。主要是基于三相电压、电流有一定关系,不是完全独立的:比如在星形连接中,ia+ib+ic=0i_a+i_b+i_c=0ia+ib+ic=0,所以知道两相的值就可以求得另一相的值;三相电流实际只需要两个量来表示。(具体原理可以参考其他文章,比如,手撕系列(2):Clark变换与Park变换 - 知乎 (zhihu.com))
这里强调定子αβ静止坐标系,是因为转子的变量经过3/2变换后,是在
相对转子静止的转子αβ坐标系上,而这个坐标系(后面按照参考书的方式称为转子DQ坐标系)相对定子αβ静止坐标系以转子的电角速度ωr\omega_rωr旋转
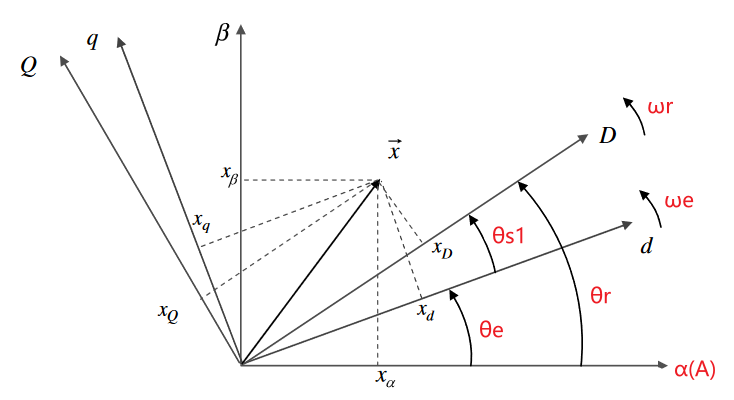
abc三相坐标系、定子αβ静止坐标系、转子DQ坐标系、同步dq坐标系的关系:
- abc三相坐标系没画全,a轴和α轴重合。
- 转子DQ坐标系和同步dq坐标系都是在旋转的,角速度如下。
这里使用等幅值变换,并且A轴和α轴重合:
[xαxβx0]=T3/2[xaxbxc]=23[1−12−12032−32121212][xaxbxc]\left[ \begin{matrix} x_\alpha \\ x_\beta \\ x_0 \end{matrix} \right] =T_{3/2}\left[ \begin{matrix} x_a \\ x_b \\ x_c \end{matrix} \right]= \frac{2}{3} \left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix} \right] \left[ \begin{matrix} x_a \\ x_b \\ x_c \end{matrix} \right] xαxβx0=T3/2xaxbxc=321021−212321−21−2321xaxbxc
变换矩阵把第三行也加上,只是为了后面便于计算逆矩阵。
使用矢量表示
一些推导在矢量表示下更方便。
举例如下:
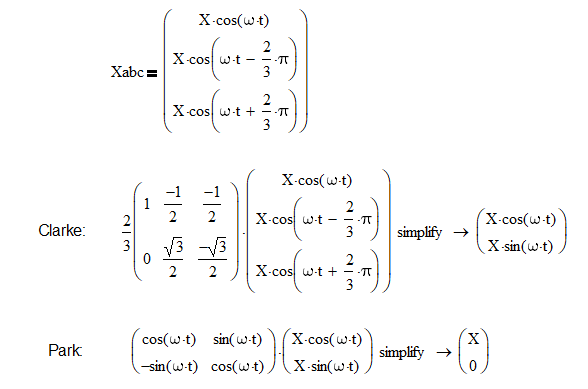
[Xcos(ωt)Xcos(ωt−23π)Xcos(ωt+23π)]→T3/2[Xcos(ωt)Xsin(ωt)]→Tαβ/dq[X0]\left[ \begin{matrix} Xcos(\omega t) \\ Xcos(\omega t-\frac{2}{3}\pi) \\Xcos(\omega t+\frac{2}{3}\pi) \end{matrix} \right] \xrightarrow{T_{3/2}} \left[ \begin{matrix} Xcos(\omega t) \\ Xsin(\omega t) \end{matrix} \right] \xrightarrow{T_{\alpha\beta/dq}} \left[ \begin{matrix} X \\ 0 \end{matrix} \right] Xcos(ωt)Xcos(ωt−32π)Xcos(ωt+32π)T3/2[Xcos(ωt)Xsin(ωt)]Tαβ/dq[X0]
这个过程也可以用矢量表示为:
[Xcos(ωt)Xcos(ωt−23π)Xcos(ωt+23π)]→T3/2X⃗αβ=Xcos(ωt)+jXsin(ωt)=Xejωt→e−jωtX⃗dq=X\begin{align*} \left[ \begin{matrix} Xcos(\omega t) \\ Xcos(\omega t-\frac{2}{3}\pi) \\Xcos(\omega t+\frac{2}{3}\pi) \end{matrix} \right] \xrightarrow{T_{3/2}} & \vec{X}^{\alpha\beta}=Xcos(\omega t) + jXsin(\omega t)=Xe^{j\omega t} \\ \xrightarrow{e^{-j\omega t}} & \vec{X}^{dq}=X \end{align*} Xcos(ωt)Xcos(ωt−32π)Xcos(ωt+32π)T3/2e−jωtXαβ=Xcos(ωt)+jXsin(ωt)=XejωtXdq=X
- 经过Clarke变换后,把α轴分量作为实部,β轴分量作为虚部,平衡的三相信号可以表示为一个在αβ坐标系逆时针旋转的矢量,矢量的模等于X(因为等幅值变换),角速度为ω\omegaω,角度为 ωt\omega tωt。
- 如果采用dq同步坐标系,就是说让坐标系与信号同步旋转,在dq坐标系下,三相信号最终变成了一个静止的矢量。
- 注意αβ->dq变换(Park变换)是对信号做运算,其目的是把信号变换到一个
逆时针旋转,角速度也为ω\omegaω的dq坐标系上。而对于信号而言,让坐标轴逆时针旋转,其实就是让信号顺时针旋转,从而抵消在静止坐标系下的角速度,最终得到直流量。这也就是park变换被表示为e−jωte^{-j\omega t}e−jωt的原因。(因为需要用到,把park变换也简单介绍一下)
电压方程(矢量形式)
对定子电压做3/2变换:
[uαuβu0]=T3/2[uAuBuC]=T3/2[Rs000Rs000Rs]T3/2−1⋅T3/2[iAiBiC]+T3/2ddt[ψAψBψC]=[Rs000Rs000Rs][iαiβi0]+ddt[ψαψβψ0]\begin{align*} \left[ \begin{matrix} u_\alpha \\ u_\beta \\u_0 \end{matrix} \right] = T_{3/2}\left[\begin{matrix} u_A \\ u_B \\ u_C \end{matrix}\right] &= T_{3/2} \left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right] T_{3/2}^{-1}\cdot T_{3/2} \left[\begin{matrix} i_A \\ i_B \\ i_C \end{matrix}\right] + T_{3/2} \frac{d}{dt}\left[\begin{matrix} \psi_A \\ \psi_B \\ \psi_C \end{matrix}\right] \\ &=\left[\begin{matrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{matrix}\right]\left[ \begin{matrix} i_\alpha \\ i_\beta \\ i_0 \end{matrix} \right] + \frac{d}{dt}\left[\begin{matrix} \psi_\alpha \\ \psi_\beta \\ \psi_0 \end{matrix}\right] \end{align*} uαuβu0=T3/2uAuBuC=T3/2Rs000Rs000RsT3/2−1⋅T3/2iAiBiC+T3/2dtdψAψBψC=Rs000Rs000Rsiαiβi0+dtdψαψβψ0
注意矩阵中间的 T3/2−1⋅T3/2=ET_{3/2}^{-1}\cdot T_{3/2}=ET3/2−1⋅T3/2=E,(单位矩阵)。计算时,T3/2−1T_{3/2}^{-1}T3/2−1和前面结合,T3/2T_{3/2}T3/2和后面的电流向量结合,实现αβ转换。
只看前两行,写成矢量形式:
u⃗s=Rsi⃗s+ddtψ⃗s\vec{u}_s=R_s\vec{i}_s+\frac{d}{dt}\vec{\psi}_s us=Rsis+dtdψs
从这个方程可以看出,定子电压u⃗s\vec{u}_sus的相位超前定子磁链ψ⃗s\vec{\psi}_sψs 约90°(如果忽略RsR_sRs)
转子电压和定子电压表达式类似,做3/2变换,省略中间过程,写成矢量形式:
u⃗rr=Rri⃗rr+ddtψ⃗rr\vec{u}_r^r=R_r\vec{i}_r^r+\frac{d}{dt}\vec{\psi}_r^r urr=Rrirr+dtdψrr
注意转子物理量的上标r。此时转子坐标系与定子坐标系不同。
只经过3/2变换,转子的物理量位于相对转子静止的坐标系上(参考书中称为大写的DQ坐标系),而这个坐标系以转子的电角速度ωr\omega_rωr旋转,与定子坐标系的夹角为ωrt\omega_rtωrt。
目标是把转子的物理量也放到定子αβ静止坐标系中。所以,需要把转子的坐标系旋转−ωrt-\omega_rt−ωrt,相对地,也就是把转子的物理量旋转ωrt\omega_rtωrt。(有点绕)。这样处理以后,把上标r去掉,表示定子和转子的物理量是在同一个坐标系中(定子αβ静止坐标系):
u⃗r=u⃗rrejωrt=Rri⃗rrejωrt+ejωrtddtψ⃗rr=Rri⃗r+ddtψ⃗r−jωrψ⃗r\begin{align*} \vec{u}_r=\vec{u}_r^re^{j\omega_r t} &=R_r\vec{i}_r^re^{j\omega_r t}+e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r \\ &=R_r\vec{i}_r+\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{align*} ur=urrejωrt=Rrirrejωrt+ejωrtdtdψrr=Rrir+dtdψr−jωrψr
备注:
1.推导过程其实是复合函数的求导
ψ⃗r=ejωrtψ⃗rr,ddtψ⃗r=dejωrtψ⃗rrdt=ejωrtddtψ⃗rr+ψ⃗rrdejωrtdt=ejωrtddtψ⃗rr+ψ⃗rr(jωrejωrt)=ejωrtddtψ⃗rr+jωrψ⃗r→ejωrtddtψ⃗rr=ddtψ⃗r−jωrψ⃗r\begin{align*} \vec{\psi}_r&=e^{j\omega_r t}\vec{\psi}_r^r, \\ \frac{d}{dt}\vec{\psi}_r &=\frac{de^{j\omega_r t}\vec{\psi}_r^r}{dt} =e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r+\vec{\psi}_r^r\frac{de^{j\omega_r t}}{dt} \\ &=e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r+\vec{\psi}_r^r (j\omega_r e^{j\omega_r t}) \\ &= e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r + j\omega_r\vec{\psi}_r \\ \rightarrow &e^{j\omega_r t}\frac{d}{dt}\vec{\psi}_r^r =\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{align*} ψrdtdψr→=ejωrtψrr,=dtdejωrtψrr=ejωrtdtdψrr+ψrrdtdejωrt=ejωrtdtdψrr+ψrr(jωrejωrt)=ejωrtdtdψrr+jωrψrejωrtdtdψrr=dtdψr−jωrψr
2.−jωrψ⃗r-j\omega_r\vec{\psi}_r−jωrψr导致转子物理量的αβ分量之间存在耦合
3.转子物理量的角频率为 ωs1=ωe−ωr\omega_{s1}=\omega_e-\omega_rωs1=ωe−ωr。(例如,转子电流的角速度=转差角速度=定子(电网)角速度-转子电角速度)。在转子的DQ坐标系中,转子的物理量可以表示为Xejωs1tXe^{j\omega_{s1}t}Xejωs1t。转换到定子αβ静止坐标系,转子的物理量变为Xejωs1tejωrt=XejωetXe^{j\omega_{s1}t}e^{j\omega_r t}=Xe^{j\omega_{e}t}Xejωs1tejωrt=Xejωet。也就是说,在定子αβ静止坐标系,转子和定子的物理量具有相同的频率。
整理电压方程的矢量形式如下:
{u⃗s=Rsi⃗s+ddtψ⃗su⃗r=Rri⃗r+ddtψ⃗r−jωrψ⃗r\begin{cases} \vec{u}_s=R_s\vec{i}_s+\frac{d}{dt}\vec{\psi}_s \\ \vec{u}_r=R_r\vec{i}_r+\frac{d}{dt}\vec{\psi}_r-j\omega_r\vec{\psi}_r \end{cases} {us=Rsis+dtdψsur=Rrir+dtdψr−jωrψr
电压方程(αβ形式)
让矢量的实部和虚部分别相等,把电压方程写成αβ形式:
{usα=Rsisα+ddtψsαusβ=Rsisβ+ddtψsβurα=Rrirα+ddtψrα+ωrψrβurβ=Rrirβ+ddtψrβ−ωrψrα\begin{cases} u_{s\alpha} &= R_si_{s\alpha}+\frac{d}{dt}\psi_{s\alpha}\\ u_{s\beta} &= R_si_{s\beta}+\frac{d}{dt}\psi_{s\beta}\\ u_{r\alpha} &= R_ri_{r\alpha}+\frac{d}{dt}\psi_{r\alpha}+\omega_r\psi_{r\beta}\\ u_{r\beta} &= R_ri_{r\beta}+\frac{d}{dt}\psi_{r\beta}-\omega_r\psi_{r\alpha} \end{cases} ⎩⎨⎧usαusβurαurβ=Rsisα+dtdψsα=Rsisβ+dtdψsβ=Rrirα+dtdψrα+ωrψrβ=Rrirβ+dtdψrβ−ωrψrα
注意转子电压方程中的耦合项。
磁链方程(αβ形式)
磁链方程不知道怎么样直接用矢量来做。。所以还是先αβ形式再矢量形式吧。
对比矢量形式和矩阵形式(其中 ωrt=θr\omega_r t=\theta_rωrt=θr)
i⃗r=ejθri⃗rr,i⃗rr=e−jθri⃗rrirαβ=Tr(θr)irr,irr=Tr(−θr)irαβ\begin{align*} \vec{i}_{r}&=e^{j\theta_r}\vec{i}_{r}^r,\quad\; \vec{i}_{r}^r=e^{-j\theta_r}\vec{i}_{r}^r \\ \boldsymbol{i}_{r\alpha\beta}&=T_{r}(\theta_r)\boldsymbol{i}_{r}^r, \; \boldsymbol{i}_{r}^r = T_{r}(-\theta_r)\boldsymbol{i}_{r\alpha\beta} \end{align*} irirαβ=ejθrirr,irr=e−jθrirr=Tr(θr)irr,irr=Tr(−θr)irαβ
其中,Tr(θr)T_{r}(\theta_r)Tr(θr)实现逆时针旋转θr\theta_rθr(park反变换),Tr(−θr)T_{r}(-\theta_r)Tr(−θr)实现顺时针旋转θr\theta_rθr(park变换)。(都写成3x3矩阵,便于运算)
Tr(θr)=[cosθr−sinθr0sinθrcosθr0001],(inversePark)Tr(−θr)=[cosθrsinθr0−sinθrcosθr0001],(Park)Tr−1(θr)=Tr(−θr)\begin{align*} T_{r}(\theta_r) &= \left[\begin{matrix} cos\theta_r & -sin\theta_r & 0\\ sin\theta_r & cos\theta_r & 0 \\ 0 & 0 & 1 \end{matrix} \right], \;(\text{inverse\,Park}) \\ T_{r}(-\theta_r) &= \left[\begin{matrix} cos\theta_r & sin\theta_r & 0\\ -sin\theta_r & cos\theta_r & 0 \\ 0 & 0 & 1 \end{matrix} \right], \;(\text{Park}) \\ T_{r}^{-1}(\theta_r) &= T_{r}(-\theta_r) \end{align*} Tr(θr)Tr(−θr)Tr−1(θr)=cosθrsinθr0−sinθrcosθr0001,(inversePark)=cosθr−sinθr0sinθrcosθr0001,(Park)=Tr(−θr)
补充一些用到的式子:
- 矩阵乘法:MTAB=MTA[(MT)−1MT]B=MTAT−1M−1(MTB)MTAB=MTA[(MT)^{-1}MT]B=MTAT^{-1}M^{-1}(MTB)MTAB=MTA[(MT)−1MT]B=MTAT−1M−1(MTB)
- 定子侧物理量的Clarke变换:T3/2xs=xsαβT_{3/2}\boldsymbol{x}_s=\boldsymbol{x}_{s\alpha\beta}T3/2xs=xsαβ
- 转子侧物理量的Clarke变换:T3/2xr=xsαβrT_{3/2}\boldsymbol{x}_r=\boldsymbol{x}_{s\alpha\beta}^rT3/2xr=xsαβr
- 转子侧物理量Clarke变换后,再变换到定子αβ坐标系上:Tr(θr)T3/2xr=Trθrxsαβr=xsαβT_r({\theta_r})T_{3/2}\boldsymbol{x}_r=T_r{\theta_r}\boldsymbol{x}_{s\alpha\beta}^r=\boldsymbol{x}_{s\alpha\beta}Tr(θr)T3/2xr=Trθrxsαβr=xsαβ
之前三相坐标系下的磁链表达式为:
[ψsψr]=[LssLsr(θr)Lrs(θr)Lrr][isir]\left[\begin{matrix} \boldsymbol{\psi}_s \\ \boldsymbol{\psi}_r \end{matrix}\right] = \left[\begin{matrix} \boldsymbol{L}_{ss} & \boldsymbol{L}_{sr}(\theta_r) \\ \boldsymbol{L}_{rs}(\theta_r) & \boldsymbol{L}_{rr} \end{matrix}\right] \left[\begin{matrix} \boldsymbol{i}_s \\ \boldsymbol{i}_r \end{matrix}\right] [ψsψr]=[LssLrs(θr)Lsr(θr)Lrr][isir]
先把定子磁链变换到定子αβ坐标系ψsαβ\boldsymbol{\psi}_{s\alpha\beta}ψsαβ(注意其中转子电流的表达式):
ψsαβ=T3/2ψs=T3/2LssT3/2−1(T3/2is)+T3/2Lsr(θr)T3/2−1(T3/2ir)=T3/2LssT3/2−1isαβ+T3/2Lsr(θr)T3/2−1irr=(T3/2LssT3/2−1)isαβ+[T3/2Lsr(θr)T3/2−1Tr(−θr)]irαβ\begin{align*} \boldsymbol{\psi}_{s\alpha\beta}=T_{3/2}\boldsymbol{\psi}_s &= T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_s) +T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_r) \\ &=T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1}\boldsymbol{i}_{s\alpha\beta}+ T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}\boldsymbol{i}_r^r \\ &=(T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1})\boldsymbol{i}_{s\alpha\beta}+ \left[T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}T_{r}(-\theta_r) \right]\boldsymbol{i}_{r\alpha\beta} \\ \end{align*} ψsαβ=T3/2ψs=T3/2LssT3/2−1(T3/2is)+T3/2Lsr(θr)T3/2−1(T3/2ir)=T3/2LssT3/2−1isαβ+T3/2Lsr(θr)T3/2−1irr=(T3/2LssT3/2−1)isαβ+[T3/2Lsr(θr)T3/2−1Tr(−θr)]irαβ
其中,两个电感矩阵在变换后变为:
T3/2LssT3/2−1=[1.5Lm+Lls0001.5Lm+Lls000Lls]T3/2Lsr(θr)T3/2−1Tr(−θr)=[1.5Lm0001.5Lm0000]\begin{align*} T_{3/2}\boldsymbol{L}_{ss}T_{3/2}^{-1} &= \left[\begin{matrix} 1.5L_m+L_{ls} & 0 & 0 \\ 0 & 1.5L_m+L_{ls} & 0 \\ 0 & 0 & L_{ls} \end{matrix}\right] \\ T_{3/2}\boldsymbol{L}_{sr}(\theta_r) T_{3/2}^{-1}T_{r}(-\theta_r) &= \left[\begin{matrix} 1.5L_m & 0 & 0 \\ 0 & 1.5L_m & 0 \\ 0 & 0 & 0 \end{matrix}\right] \\ \end{align*} T3/2LssT3/2−1T3/2Lsr(θr)T3/2−1Tr(−θr)=1.5Lm+Lls0001.5Lm+Lls000Lls=1.5Lm0001.5Lm0000
在mathCAD中的计算结果:
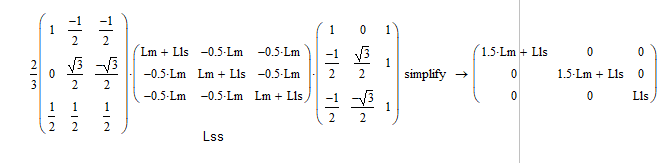
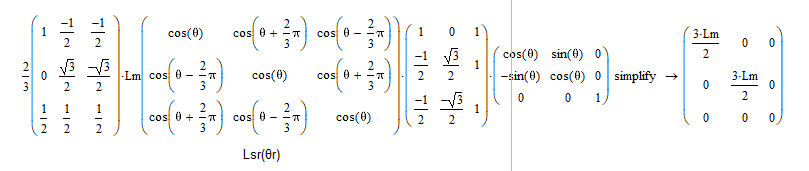
第二行,转子磁链 ψrαβ\boldsymbol{\psi}_{r\alpha\beta}ψrαβ,需要在Clark变换后,再转过θr\theta_rθr(左乘 Tr(θr)T_{r}(\theta_r)Tr(θr)),才转换到αβ定子坐标系下。
ψrαβ=Tr(θr)ψrαβr=Tr(θr)T3/2ψr=Tr(θr)T3/2Lrs(θr)T3/2−1(T3/2is)+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)][Tr(θr)T3/2ir]=Tr(θr)T3/2Lrs(θr)T3/2−1isαβ+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)]irαβ\begin{align*} \boldsymbol{\psi}_{r\alpha\beta} &= T_{r}(\theta_r)\boldsymbol{\psi}_{r\alpha\beta}^r =T_{r}(\theta_r)T_{3/2}\boldsymbol{\psi}_r \\ &= T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1}(T_{3/2}\boldsymbol{i}_s) + \left[T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r)\right] \left[ T_{r}(\theta_r)T_{3/2}\boldsymbol{i}_r \right]\\ &= T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1}\boldsymbol{i}_{s\alpha\beta} + \left[T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r)\right] \boldsymbol{i}_{r\alpha\beta}\\ \end{align*} ψrαβ=Tr(θr)ψrαβr=Tr(θr)T3/2ψr=Tr(θr)T3/2Lrs(θr)T3/2−1(T3/2is)+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)][Tr(θr)T3/2ir]=Tr(θr)T3/2Lrs(θr)T3/2−1isαβ+[Tr(θr)T3/2LrrT3/2−1Tr(−θr)]irαβ
其中,两个电感矩阵在变换后变为:
Tr(θr)T3/2Lrs(θr)T3/2−1=[1.5Lm0001.5Lm0000]Tr(θr)T3/2LrrT3/2−1Tr(−θr)=[1.5Lm+Llr0001.5Lm+Llr000Llr]\begin{align*} T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rs}(\theta_r) T_{3/2}^{-1} &= \left[\begin{matrix} 1.5L_m & 0 & 0 \\ 0 & 1.5L_m & 0 \\ 0 & 0 & 0 \end{matrix}\right] \\ T_{r}(\theta_r)T_{3/2}\boldsymbol{L}_{rr}T_{3/2}^{-1}T_{r}(-\theta_r) &= \left[\begin{matrix} 1.5L_m+L_{lr} & 0 & 0 \\ 0 & 1.5L_m+L_{lr} & 0 \\ 0 & 0 & L_{lr} \end{matrix}\right] \\ \end{align*} Tr(θr)T3/2Lrs(θr)T3/2−1Tr(θr)T3/2LrrT3/2−1Tr(−θr)=1.5Lm0001.5Lm0000=1.5Lm+Llr0001.5Lm+Llr000Llr
在mathCAD中的计算结果:
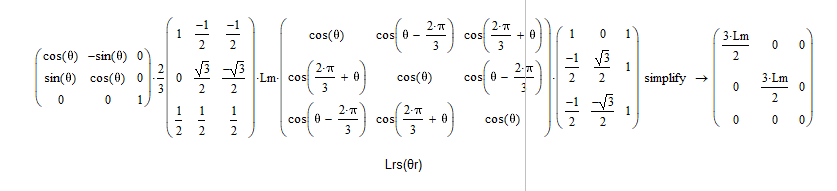
(第二个矩阵表达式比较长,分两步计算)

只看前两行,这些电感矩阵在变换后都变成了对角矩阵,并且系数都变成了常数(不再有cos(θr)cos(\theta_r)cos(θr)项),模型得到了简化。
{ψsα=(1.5Lm+Lls)isα+1.5Lmirα=Lsisα+LMirαψsβ=(1.5Lm+Lls)isβ+1.5Lmirβ=Lsisβ+LMirβψrα=(1.5Lm+Llr)irα+1.5Lmisα=Lrirα+LMisαψrβ=(1.5Lm+Llr)irβ+1.5Lmisβ=Lrirβ+LMisβ\begin{cases} \psi_{s\alpha} &= (1.5L_m+L_{ls})i_{s\alpha}+1.5L_mi_{r\alpha} =L_si_{s\alpha}+L_Mi_{r\alpha}\\ \psi_{s\beta} &= (1.5L_m+L_{ls})i_{s\beta}+1.5L_mi_{r\beta} =L_si_{s\beta}+L_Mi_{r\beta}\\ \psi_{r\alpha} &= (1.5L_m+L_{lr})i_{r\alpha}+1.5L_mi_{s\alpha} =L_ri_{r\alpha}+L_Mi_{s\alpha}\\ \psi_{r\beta} &= (1.5L_m+L_{lr})i_{r\beta}+1.5L_mi_{s\beta} =L_ri_{r\beta}+L_Mi_{s\beta} \end{cases} ⎩⎨⎧ψsαψsβψrαψrβ=(1.5Lm+Lls)isα+1.5Lmirα=Lsisα+LMirα=(1.5Lm+Lls)isβ+1.5Lmirβ=Lsisβ+LMirβ=(1.5Lm+Llr)irα+1.5Lmisα=Lrirα+LMisα=(1.5Lm+Llr)irβ+1.5Lmisβ=Lrirβ+LMisβ
磁链方程(矢量形式)
根据磁链方程的αβ形式可以写出矢量形式。
{ψ⃗s=Lsi⃗s+LMi⃗rψ⃗r=Lri⃗r+LMi⃗s\begin{cases} \vec{\psi}_{s} &=L_s\vec{i}_{s}+L_M\vec{i}_{r}\\ \vec{\psi}_{r} &=L_r\vec{i}_{r}+L_M\vec{i}_{s} \end{cases} {ψsψr=Lsis+LMir=Lrir+LMis
dq坐标系模型
回顾之前的推导,在定子αβ静止坐标系,转子和定子的物理量具有相同的频率,也就是ωe\omega_eωe。所以,在dq坐标系的转速为ωe\omega_eωe时,
一些物理量会变成直流量,便于控制。之前也提到了,让坐标轴逆时针旋转ωet\omega_e tωet,就是把对应的物理量顺时针旋转ωet\omega_e tωet,也就是e−jωtx⃗e^{-j\omega t}\vec{x}e−jωtx
矢量形式
把定子αβ静止坐标系的电压方程两边都乘以e−jωte^{-j\omega t}e−jωt,得到# dq坐标系下的电压方程:
电压方程中,e−jωtu⃗s=u⃗sae^{-j\omega t}\vec{u}_s=\vec{u}_s^ae−jωtus=usa。上标a代表dq轴下的物理量。
注意对于磁链的微分,略有不同,之前推导过:e−jωetddtψ⃗=ddtψ⃗a+jωeψ⃗ae^{-j\omega_e t}\frac{d}{dt}\vec{\psi}=\frac{d}{dt}\vec{\psi}^a+j\omega_e\vec{\psi}^ae−jωetdtdψ=dtdψa+jωeψa
记得角速度的关系:ωe=ωs1+ωr\omega_e=\omega_{s1}+\omega_{r}ωe=ωs1+ωr,电网速度=转差速度+转子电角速度。其中,转子物理量(电压、电流、磁链)的角速度就是转差速度ωs1\omega_{s1}ωs1,所以这个方程是还挺对称的。
{u⃗sa=Rsi⃗sa+ddtψ⃗sa+jωeψ⃗sau⃗ra=Rri⃗ra+ddtψ⃗ra+j(ωe−ωr)ψ⃗ra=Rri⃗ra+ddtψ⃗ra+jωs1ψ⃗ra\begin{cases} \vec{u}_s^a=R_s\vec{i}_s^a+\frac{d}{dt}\vec{\psi}_s^a+j\omega_e \vec{\psi}_s^a \\ \vec{u}_r^a=R_r\vec{i}_r^a+\frac{d}{dt}\vec{\psi}_r^a+j(\omega_e-\omega_r)\vec{\psi}_r^a = R_r\vec{i}_r^a+\frac{d}{dt}\vec{\psi}_r^a+j\omega_{s1}\vec{\psi}_r^a \end{cases} {usa=Rsisa+dtdψsa+jωeψsaura=Rrira+dtdψra+j(ωe−ωr)ψra=Rrira+dtdψra+jωs1ψra
磁链方程形式没有变,只是上标加了个a,表示是dq轴下的量。
{ψ⃗sa=Lsi⃗sa+LMi⃗raψ⃗ra=Lri⃗ra+LMi⃗sa\begin{cases} \vec{\psi}_{s}^a &=L_s\vec{i}_{s}^a+L_M\vec{i}_{r}^a\\ \vec{\psi}_{r}^a &=L_r\vec{i}_{r}^a+L_M\vec{i}_{s}^a \end{cases} {ψsaψra=Lsisa+LMira=Lrira+LMisa
αβ形式
根据矢量形式,同样可以写出αβ形式。
电压方程:
{usd=Rsisd+ddtψsd−ωeψsqusq=Rsisq+ddtψsq+ωeψsdurd=Rrird+ddtψrd−ωs1ψrqurq=Rrirq+ddtψrq+ωs1ψrd\begin{cases} u_{sd} &= R_si_{sd}+\frac{d}{dt}\psi_{sd}-\omega_e\psi_{sq}\\ u_{sq} &= R_si_{sq}+\frac{d}{dt}\psi_{sq}+\omega_e\psi_{sd}\\ u_{rd} &= R_ri_{rd}+\frac{d}{dt}\psi_{rd}-\omega_{s1}\psi_{rq}\\ u_{rq} &= R_ri_{rq}+\frac{d}{dt}\psi_{rq}+\omega_{s1}\psi_{rd} \end{cases} ⎩⎨⎧usdusqurdurq=Rsisd+dtdψsd−ωeψsq=Rsisq+dtdψsq+ωeψsd=Rrird+dtdψrd−ωs1ψrq=Rrirq+dtdψrq+ωs1ψrd
磁链方程:
{ψsd=Lsisd+LMirdψsq=Lsisq+LMirqψrd=Lrird+LMisdψrq=Lrirq+LMisq\begin{cases} \psi_{sd} &=L_si_{sd}+L_Mi_{rd}\\ \psi_{sq} &=L_si_{sq}+L_Mi_{rq}\\ \psi_{rd} &=L_ri_{rd}+L_Mi_{sd}\\ \psi_{rq} &=L_ri_{rq}+L_Mi_{sq} \end{cases} ⎩⎨⎧ψsdψsqψrdψrq=Lsisd+LMird=Lsisq+LMirq=Lrird+LMisd=Lrirq+LMisq
参考资料
- 第十一讲 风力发电系统基本结构+双馈电机数学模型第一部分_哔哩哔哩_bilibili11~16讲和DFIG有关,可以看下。
- G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.
- 自己买的中文书,讲得比较简略,如果只看这两本,我是看不懂的:
- 马宏伟,风力发电系统控制原理
- 王毅,风力发电系统的建模与仿真