文章目录

前言
一、EventBus使用
二、EventBus事件流程分析
- 1.注册订阅者
- 2.发布事件Event
- 3.接收事件Event
- 4.取消注册订阅者
三、发送粘性事件
问答
- - EventBus 以及它的优点
  - EventBus原理
- EventBus中设计模式
- - 为什么要使用 EventBus 来替代广播呢？
  - 说下 5 种线程模式的区别
  - EventBus 是如何做到发送粘性消息的
  - EventBus2.x的版本和3.x区别
  - RxBus 与 EventBus 比较
  - 为什么会有LiveDataBus呢
  - 常用消息总线考量
总结
致谢

前言

EventBus是一个Android/Java平台基于订阅与发布的通信框架，可以用于Activities， Fragments， Threads， Services等组件的通信，也可以用于多线程通信。优点是开销小、使用简单、以及解耦事件发送者和接收者。

Android中除了EventBus这种应用通信方式外，还有哪些手段呢？

BroadcastReceiver/LocalBroadcastReceiver：跨域广播和局域广播，跨域广播可以用来做跨进程通信。局域广播也是基于Handler实现，可以用来在应用内通信。
Handler：这个方式的弊端在于通信消息难以管理。
接口回调：接口回调的好处是比较清晰明显，但是如果涉及到大量页面的跳转或者通信场景比较复杂，这种方式就变得难以维护，耦合较高。

EventBus版本信息

官方网站：https://github.com/greenrobot/EventBus
源码版本：3.1.1

一、EventBus使用

官网图片
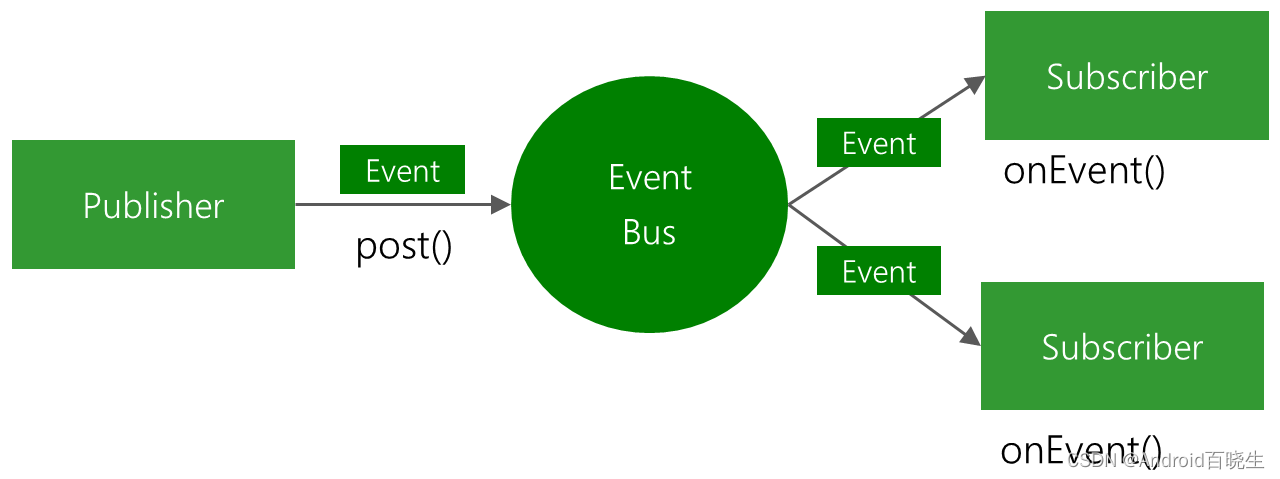
我们先来一个简单的Demo，从Demo入手分析事件的订阅和发布流程。

public class MainActivity extends AppCompatActivity implements View.OnClickListener{@Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);setContentView(R.layout.activity_main);findViewById(R.id.btn_post_event).setOnClickListener(this);}@Overrideprotected void onStart() {super.onStart();// 订阅事件EventBus.getDefault().register(this);}@Overrideprotected void onStop() {super.onStop();// 取消订阅s事件EventBus.getDefault().unregister(this);}// 接收事件Event@Subscribe(threadMode = ThreadMode.MAIN)public void onEvent(Event event) {Toast.makeText(this, event.getMessage(), Toast.LENGTH_SHORT).show();}@Overridepublic void onClick(View v) {switch (v.getId()){case R.id.btn_post_event:// 发布事件EventEventBus.getDefault().post(new Event("Event Message"));break;}}
}

具体实现细节，我们接下来深入源码中去查看。

二、EventBus事件流程分析

我们先来看一下EventBus的源码结构，如下所示：
在这里插入图片描述
主要包含了两个部分：

eventbus：核心库。
eventbus-annotation-processor：注解处理部分。

EventBus核心库调用流程如下：
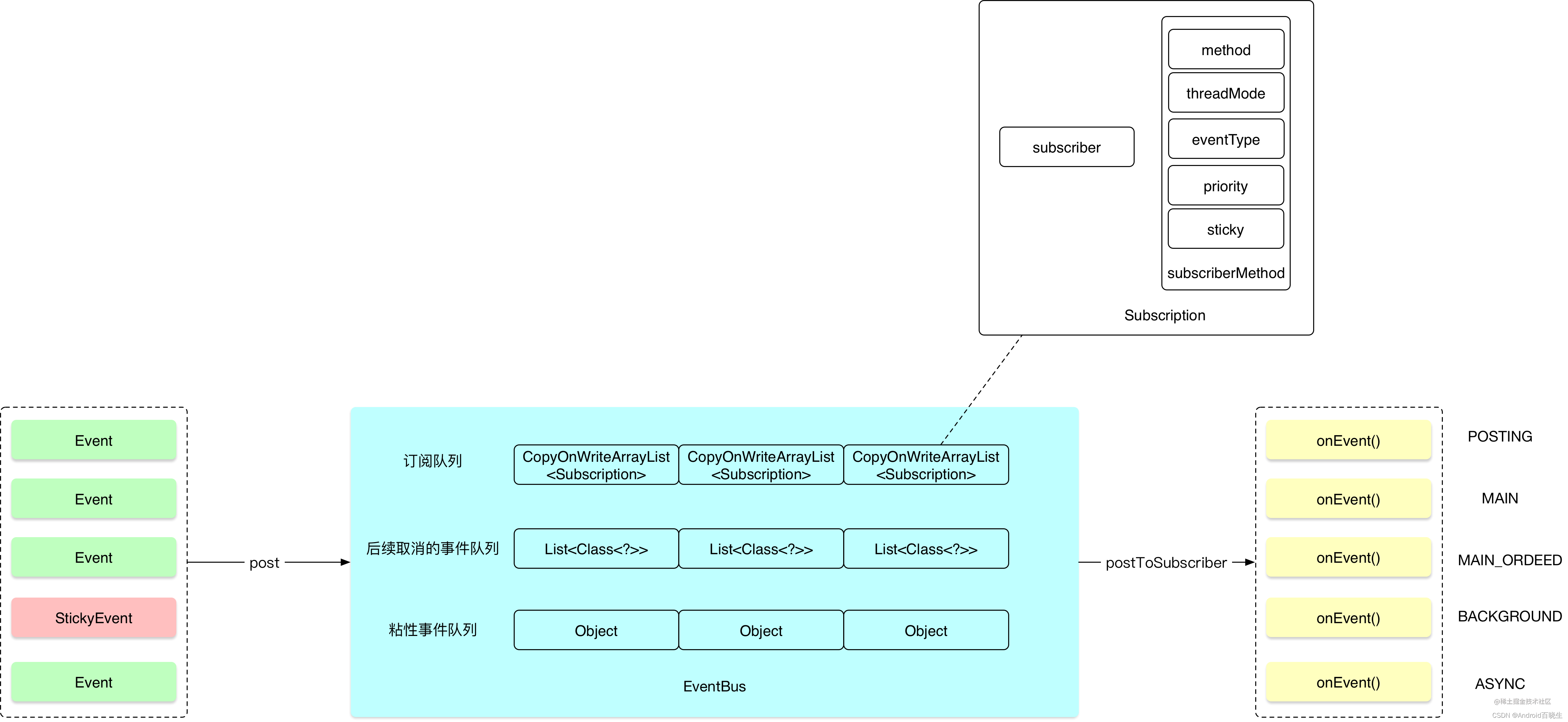
在这里插入图片描述

注册订阅者。
发布事件Event。
接收事件Event。
取消注册订阅者。

1.注册订阅者

订阅事件是通过以下方法来完成的：

EventBus.getDefault().register(this);

getDefault()用来获取EventBus实例，当然你也可以通过EventBusBuilder自己构建实例。

public class EventBus {public void register(Object subscriber) {// 1. 获取订阅者的类名。Class<?> subscriberClass = subscriber.getClass();// 2. 查找当前订阅者的所有响应函数。List<SubscriberMethod> subscriberMethods = subscriberMethodFinder.findSubscriberMethods(subscriberClass);synchronized (this) {// 3. 循环每个事件响应函数for (SubscriberMethod subscriberMethod : subscriberMethods) {subscribe(subscriber, subscriberMethod);}}}
}

SubscriberMethod用来描述onEvent()这些方法的信息，包含方法名、线程、Class类型、优先级、是否是粘性事件。

接着调用subscribe()进行事件注册，如下所示：

public class EventBus {// 订阅者队列private final Map<Class<?>, CopyOnWriteArrayList<Subscription>> subscriptionsByEventType;// 后续准备取消的事件队列private final Map<Object, List<Class<?>>> typesBySubscriber;// 粘性事件队列private final Map<Class<?>, Object> stickyEvents;private void subscribe(Object subscriber, SubscriberMethod subscriberMethod) {// 事件类型（xxxEvent）Class<?> eventType = subscriberMethod.eventType;Subscription newSubscription = new Subscription(subscriber, subscriberMethod);// 1. 获取该事件类型的所有订阅者信息。CopyOnWriteArrayList<Subscription> subscriptions = subscriptionsByEventType.get(eventType);if (subscriptions == null) {subscriptions = new CopyOnWriteArrayList<>();subscriptionsByEventType.put(eventType, subscriptions);} else {if (subscriptions.contains(newSubscription)) {throw new EventBusException("Subscriber " + subscriber.getClass() + " already registered to event "+ eventType);}}int size = subscriptions.size();// 2. 按照事件优先级将其插入订阅者列表中。for (int i = 0; i <= size; i++) {if (i == size || subscriberMethod.priority > subscriptions.get(i).subscriberMethod.priority) {subscriptions.add(i, newSubscription);break;}}// 3. 得到当前订阅者订阅的所有事件队列，存放在typesBySubscriber中，用于后续取消事件订阅。List<Class<?>> subscribedEvents = typesBySubscriber.get(subscriber);if (subscribedEvents == null) {subscribedEvents = new ArrayList<>();typesBySubscriber.put(subscriber, subscribedEvents);}subscribedEvents.add(eventType);// 4. 是否是粘性事件，如果是粘性事件，则从stickyEvents队列中取出最后一个该类型的事件发送给订阅者。if (subscriberMethod.sticky) {if (eventInheritance) {// Existing sticky events of all subclasses of eventType have to be considered.// Note: Iterating over all events may be inefficient with lots of sticky events,// thus data structure should be changed to allow a more efficient lookup// (e.g. an additional map storing sub classes of super classes: Class -> List<Class>).Set<Map.Entry<Class<?>, Object>> entries = stickyEvents.entrySet();for (Map.Entry<Class<?>, Object> entry : entries) {Class<?> candidateEventType = entry.getKey();if (eventType.isAssignableFrom(candidateEventType)) {Object stickyEvent = entry.getValue();checkPostStickyEventToSubscription(newSubscription, stickyEvent);}}} else {Object stickyEvent = stickyEvents.get(eventType);checkPostStickyEventToSubscription(newSubscription, stickyEvent);}}}}

Subscription包含了订阅者subscriber和订阅函数subscriberMethod两个信息。

2.发布事件Event

发送事件Event是通过以下方法完成的，如下所示：

EventBus.getDefault().post(new Event("Event Message"));

public class EventBus {public void post(Object event) {// 1. 获取当前线程的PostingThreadState对象，该对象包含事件队列，保存在ThreadLocal中。PostingThreadState postingState = currentPostingThreadState.get();List<Object> eventQueue = postingState.eventQueue;// 2. 将当前事件加入到该线程的事件队列中。eventQueue.add(event);// 3. 判断事件是否在分发中。如果没有则遍历事件队列进行实际分发。if (!postingState.isPosting) {postingState.isMainThread = isMainThread();postingState.isPosting = true;if (postingState.canceled) {throw new EventBusException("Internal error. Abort state was not reset");}try {while (!eventQueue.isEmpty()) {// 4. 进行事件分发。postSingleEvent(eventQueue.remove(0), postingState);}} finally {postingState.isPosting = false;postingState.isMainThread = false;}}}}

PostingThreadState用来描述发送事件的线程的相关状态信息，包含事件队列，是否是主线程、订阅者、事件Event等信息。

然后调用postSingleEvent()进行事件分发。

public class EventBus {private void postSingleEvent(Object event, PostingThreadState postingState) throws Error {Class<?> eventClass = event.getClass();boolean subscriptionFound = false;// 1. 如果事件允许继承，则查找该事件类型的所有父类和接口，依次进行循环。if (eventInheritance) {List<Class<?>> eventTypes = lookupAllEventTypes(eventClass);int countTypes = eventTypes.size();for (int h = 0; h < countTypes; h++) {Class<?> clazz = eventTypes.get(h);// 2. 查找该事件的所有订阅者。subscriptionFound |= postSingleEventForEventType(event, postingState, clazz);}} else {subscriptionFound = postSingleEventForEventType(event, postingState, eventClass);}if (!subscriptionFound) {if (logNoSubscriberMessages) {logger.log(Level.FINE, "No subscribers registered for event " + eventClass);}if (sendNoSubscriberEvent && eventClass != NoSubscriberEvent.class &&eventClass != SubscriberExceptionEvent.class) {post(new NoSubscriberEvent(this, event));}}}}

然后调用postSingleEventForEventType()方法查询当前事件的所有订阅者，如下所示：

public class EventBus {private boolean postSingleEventForEventType(Object event, PostingThreadState postingState, Class<?> eventClass) {CopyOnWriteArrayList<Subscription> subscriptions;synchronized (this) {// 1. 获取当前事件的所有订阅者。subscriptions = subscriptionsByEventType.get(eventClass);}if (subscriptions != null && !subscriptions.isEmpty()) {// 2. 遍历所有订阅者。for (Subscription subscription : subscriptions) {postingState.event = event;postingState.subscription = subscription;boolean aborted = false;try {// 3. 根据订阅者所在线程，调用事件响应函数onEvent()。postToSubscription(subscription, event, postingState.isMainThread);aborted = postingState.canceled;} finally {postingState.event = null;postingState.subscription = null;postingState.canceled = false;}if (aborted) {break;}}return true;}return false;}}

调用postToSubscription()方法根据订阅者所在线程，调用事件响应函数onEvent()，这便涉及到接收事件Event的处理了，我们接着来看。

3.接收事件Event

//EventBus.javaprivate void postToSubscription(Subscription subscription, Object event, boolean isMainThread) {//根据订阅者选择的线程模式来选择使用那种线程方式来分发处理该事件switch (subscription.subscriberMethod.threadMode) {case POSTING://直接利用反射调用订阅方法invokeSubscriber(subscription, event);break;case MAIN:if (isMainThread) {//如果当前处于主线程，直接反射调用订阅方法invokeSubscriber(subscription, event);} else {//利用Handler切换到主线程，最终还是执行invokeSubscribermainThreadPoster.enqueue(subscription, event);}break;case MAIN_ORDERED:if (mainThreadPoster != null) {//将事件入队列，在主线程上有序执行mainThreadPoster.enqueue(subscription, event);} else {// temporary: technically not correct as poster not decoupled from subscriberinvokeSubscriber(subscription, event);}break;case BACKGROUND:if (isMainThread) {//如果当前处于主线程中，将利用线程池，切换到子线程中处理，最终还是会调用invokeSubscriberbackgroundPoster.enqueue(subscription, event);} else {//如果当前处于子线程，则直接在该子线程中处理事件invokeSubscriber(subscription, event);}break;case ASYNC://无论处于什么线程，最终都是利用线程池，切换到子线程中处理，最终还是会调用invokeSubscriberasyncPoster.enqueue(subscription, event);break;default:throw new IllegalStateException("Unknown thread mode: " + subscription.subscriberMethod.threadMode);}
}void invokeSubscriber(Subscription subscription, Object event) {try {//利用反射调用订阅方法subscription.subscriberMethod.method.invoke(subscription.subscriber, event);} catch (InvocationTargetException e) {handleSubscriberException(subscription, event, e.getCause());} catch (IllegalAccessException e) {throw new IllegalStateException("Unexpected exception", e);}
}

@Subscribe(threadMode = ThreadMode.MAIN)
public void onEvent(Event event) {Toast.makeText(this, event.getMessage(), Toast.LENGTH_SHORT).show();
}

如上所示，onEvent函数上是可以加Subscribe注解了，该注解标明了onEvent()函数在哪个线程执行。主要有以下几个线程：

PostThread：默认的 ThreadMode，表示在执行 Post 操作的线程直接调用订阅者的事件响应方法，不论该线程是否为主线程（UI 线程）。当该线程为主线程时，响应方法中不能有耗时操作，否则有卡主线程的风险。适用场景：对于是否在主线程执行无要求，但若 Post 线程为主线程，不能耗时的操作；
MainThread：在主线程中执行响应方法。如果发布线程就是主线程，则直接调用订阅者的事件响应方法，否则通过主线程的 Handler 发送消息在主线程中处理，调用订阅者的事件响应函数。显然，MainThread类的方法也不能有耗时操作，以避免卡主线程。适用场景：必须在主线程执行的操作；
MAIN_ORDERED：无论在哪个线程发送事件，都会先将事件加入到队列中，然后通过 Handler 切换到主线程再执行。
BackgroundThread：在后台线程中执行响应方法。如果发布线程不是主线程，则直接调用订阅者的事件响应函数，否则启动唯一的后台线程去处理。由于后台线程是唯一的，当事件超过一个的时候，它们会被放在队列中依次执行，因此该类响应方法虽然没有PostThread类和MainThread类方法对性能敏感，但最好不要有重度耗时的操作或太频繁的轻度耗时操作，以造成其他操作等待。适用场景：操作轻微耗时且不会过于频繁，即一般的耗时操作都可以放在这里；
Async：不论发布线程是否为主线程，都使用一个空闲线程来处理。和BackgroundThread不同的是，Async类的所有线程是相互独立的，因此不会出现卡线程的问题。适用场景：长耗时操作，例如网络访问。

这里线程执行和EventBus的成员变量对应，它们都实现了Runnable与Poster接口，Poster接口定义了事件排队功能，这些本质上都是个Runnable，放在线程池里执行，如下所示：

private final Poster mainThreadPoster;
private final BackgroundPoster backgroundPoster;
private final AsyncPoster asyncPoster;
private final SubscriberMethodFinder subscriberMethodFinder;
private final ExecutorService executorService;

4.取消注册订阅者

取消注册订阅者调用的是以下方法：

EventBus.getDefault().unregister(this);

具体如下所示：

//EventBus.javapublic synchronized void unregister(Object subscriber) {// 1. 获取当前订阅者订阅的所有事件类型。List<Class<?>> subscribedTypes = typesBySubscriber.get(subscriber);if (subscribedTypes != null) {// 2. 遍历事件队列，解除事件注册。for (Class<?> eventType : subscribedTypes) {unsubscribeByEventType(subscriber, eventType);}// 3. 移除事件订阅者。typesBySubscriber.remove(subscriber);} else {logger.log(Level.WARNING, "Subscriber to unregister was not registered before: " + subscriber.getClass());}}

调用unsubscribeByEventType()移除订阅者，如下所示：

//EventBus.javaprivate void unsubscribeByEventType(Object subscriber, Class<?> eventType) {// 1. 获取所有订阅者信息。List<Subscription> subscriptions = subscriptionsByEventType.get(eventType);if (subscriptions != null) {// 2. 遍历订阅者int size = subscriptions.size();for (int i = 0; i < size; i++) {Subscription subscription = subscriptions.get(i);// 3. 移除该订阅对象。if (subscription.subscriber == subscriber) {subscription.active = false;subscriptions.remove(i);i--;size--;}}}
}

以上便是EventBus核心的实现，相对还是比较简单的。

三、发送粘性事件

如果你在发送普通事件前没有注册过订阅者，那么这时你发送的事件是不会被接收执行的，这个事件也就被回收了。

而粘性事件就不一样了，你可以在发送粘性事件后，再去注册订阅者，一旦完成订阅，这个订阅者就会接收到这个粘性事件。与发送普通事件不同，粘性事件使用postSticky()方法来发送：

EventBus.getDefault().postSticky(new MessageEvent("Hello everyone!"));

让我们从源码中看看，是如何实现的：

/*** 用来存放粘性事件** key -> 粘性事件的类对象* value -> 粘性事件*/
private final Map<Class<?>, Object> stickyEvents;public void postSticky(Object event) {synchronized (stickyEvents) {stickyEvents.put(event.getClass(), event);}// Should be posted after it is putted, in case the subscriber wants to remove immediatelypost(event);
}

用了一个stickyEvents集合来保存粘性事件，存入后，与普通事件一样同样调用post()方法。
这里有个疑问，针对上面的使用场景，我先发送粘性事件，然后再去注册订阅，这时执行post方法去发送事件，根本就没有对应的订阅者啊，肯定是发送失败的。所以，细想一下，想达到这样效果，订阅者注册订阅后应该再将这个存入下来的事件发送一下。

带着这个疑问，我们回到register -> subscribe方法：

private void subscribe(Object subscriber, SubscriberMethod subscriberMethod) {//通过订阅方法获得事件类型参数Class<?> eventType = subscriberMethod.eventType;//通过订阅者与订阅方法来构造出一个 订阅对象Subscription newSubscription = new Subscription(subscriber, subscriberMethod);....省略部分代码....//如果订阅方法支持粘性事件if (subscriberMethod.sticky) {//是否考虑事件类的层次结构，默认为trueif (eventInheritance) {Set<Map.Entry<Class<?>, Object>> entries = stickyEvents.entrySet();for (Map.Entry<Class<?>, Object> entry : entries) {Class<?> candidateEventType = entry.getKey();//eventType 是否是 candidateEventType 的父类if (eventType.isAssignableFrom(candidateEventType)) {Object stickyEvent = entry.getValue();//检查发送粘性事件checkPostStickyEventToSubscription(newSubscription, stickyEvent);}}} else {//根据事件类型获取粘性事件Object stickyEvent = stickyEvents.get(eventType);//检查发送粘性事件checkPostStickyEventToSubscription(newSubscription, stickyEvent);}}
}/***检查发送粘性事件*/
private void checkPostStickyEventToSubscription(Subscription newSubscription, Object stickyEvent) {//如果粘性事件不为空，发送事件if (stickyEvent != null) {  postToSubscription(newSubscription, stickyEvent, isMainThread());}
}

果真，订阅者在注册订阅方法中，如果当前订阅方法支持粘性事件，则会去stickyEvents集合中查件是否有对应的粘性事件，如果找到粘性事件，则发送该事件。

问答

EventBus 以及它的优点

EventBus 是一个 Android 事件发布/订阅框架，主要用来简化 Activity、Fragment、Service、线程等之间的通讯。
优点：开销小、使用简单、以及解耦事件发送者和接收者。
缺点：原理实现复杂，无法混淆，需要手动绑定生命周期（所以后面有了LiveDataBus）。

EventBus原理

注册：通过反射获取注册类上所有的订阅方法，然后将这些订阅方法进行包装保存到 subscriptionsByEventType 集合。这里还用 typesBySubscriber 集合保存了事件类型集合，用来判断某个对象是否注册过。
解注册：注册的时候使用 subscriptionsByEventType 集合保存了所有订阅方法信息，使用 typesBySubscriber 集合保存了所有事件类型。那么解注册的时候就是为了移除这两个集合中保存的内容。
发送普通事件：从 subscriptionsByEventType 集合中取出所有订阅方法，然后根据线程模式判断是否需要切换线程，不需要则直接通过反射调用订阅方法；需要则通过 Handler 或线程池切换到指定线程再执行。
发送粘性事件：发送粘性事件的的时候，首先会将事件保存到 stickyEvents 集合，等到注册的时候判断如果是粘性事件，则从集合中取出事件进行发送。

EventBus中设计模式

单例模式：为了避免频繁创建销毁EventBus实例所带来的开销，这里采用DCL的形似来创建单例。
建造者模式：基本上开源库都有很多参数可供用户配置，所以用建造者模式来创建EventBus实例就很合理。

为什么要使用 EventBus 来替代广播呢？

广播：广播是重量级的，消耗资源较多的方式（耗时）。如果不做处理也是不安全的（容易被捕获）。
事件总线：更节省资源、更高效，能将信息传递给原生以外的各种对象。

说下 5 种线程模式的区别

POSTING：默认模式，在哪个线程发送事件，就在哪个线程执行订阅方法。
MAIN：如果在主线程发送事件，则在主线程执行订阅方法；否则先将事件加入到队列中，然后通过 Handler 切换到主线程再执行。
MAIN_ORDERED：无论在哪个线程发送事件，都会先将事件加入到队列中，然后通过 Handler 切换到主线程再执行。
BACKGROUND：如果在子线程发送事件，则在子线程执行订阅方法，否则先将事件加入到队列中，然后通过线程池去执行。
ASYNC：无论在哪个线程发送事件，都会先将事件加入到队列中，然后通过线程池去执行。

EventBus 是如何做到发送粘性消息的

发送粘性事件的的时候，首先会将事件保存到 stickyEvents 集合，等到注册的时候判断如果是粘性事件，则从集合中取出事件再进行发送。

EventBus2.x的版本和3.x区别

2.x使用的是运行时注解,采用了反射的方式对整个注册的类的所有方法进行扫描来完成注册，因而会对性能有一定影响;
3.x使用的是编译时注解，Java文件会编译成.class文件，再对class文件进行打包等一系列处理。在编译成.class文件时，EventBus会使用EventBusAnnotationProcessor注解处理器读取@Subscribe()注解并解析、处理其中的信息，然后生成Java类来保存所有订阅者的订阅信息。这样就创建出了对文件或类的索引关系，并将其编入到apk中；
从EventBus3.0开始使用了对象池缓存减少了创建对象的开销；

RxBus 与 EventBus 比较

RxBus不是一个库，而是一个文件，实现只有短短30行代码。RxBus本身不需要过多分析，它的强大完全来自于它基于的RxJava技术。所以RxBus的优点其实也就是rxJava的优点:

RxJava的Observable有onError、onComplete等状态回调；
RxJava使用组合而非嵌套的方式，避免了回调地狱；
RxJava的线程调度设计的更加优秀，更简单易用；
RxJava可使用多种操作符来进行链式调用来实现复杂的逻辑；
RxJava的信息效率高于EventBus2.x，低于EventBus3.x；

那么技术选型时如何取舍呢？
如果项目中使用了RxJava，则使用RxBus，否则使用EventBus3.x；

为什么会有LiveDataBus呢

LiveDataBus是基于LiveData实现的类似EventBus的消息通信框架，它是基于LiveData实现的，在EventBus的基础上加入了生命周期感知，完全可以代替EventBus，RxBus；

常规消息传递优缺点对比：

Handler : 容易导致内存泄漏，空指针，高耦合，不利于维护
EventBus ：原理实现复杂，无法混淆，需要手动绑定生命周期
RxBus：依赖于RxJava，包太大，影响apk大小，app启动时间

解更多LiveDataBus可以参考官网：
https://github.com/JeremyLiao/LiveEventBus

implementation 'com.jeremyliao:live-event-bus-x:1.4.5'

常用消息总线考量

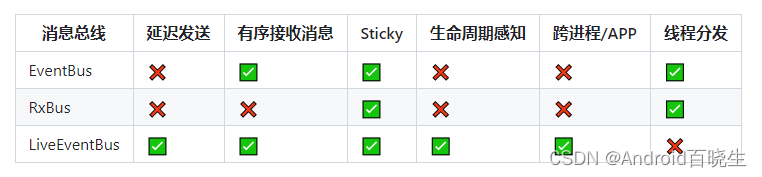
LiveEventBus官网
其实目前常用的各种事件总线xxBus原理都差不多，那么在项目中如何使用这些事件总线呢：

EventBus,RxBus: 将xxEvent消息容器和事件总线框架的依赖放到base module，其他模块组件依赖于base module; 但是这样每个模块改动都需要增删改baseModule中的消息容器, 组件化要求功能模块独立, 各组件应该尽量避免影响base module；
LiveDataBus: 无需建立消息模型，但无法想前两者一样拥有类名索引，无法引导正确的编写代码，也无法传递自定义实体到其他模块；
使用EventBus,RxBus，为了更大程度的解耦，可以独立出一个事件总线module，添加事件的实体都在这个module中，base module依赖这个事件总线module对事件通信的解耦, 抽离事件到事件总线module中减少对base module的影响；