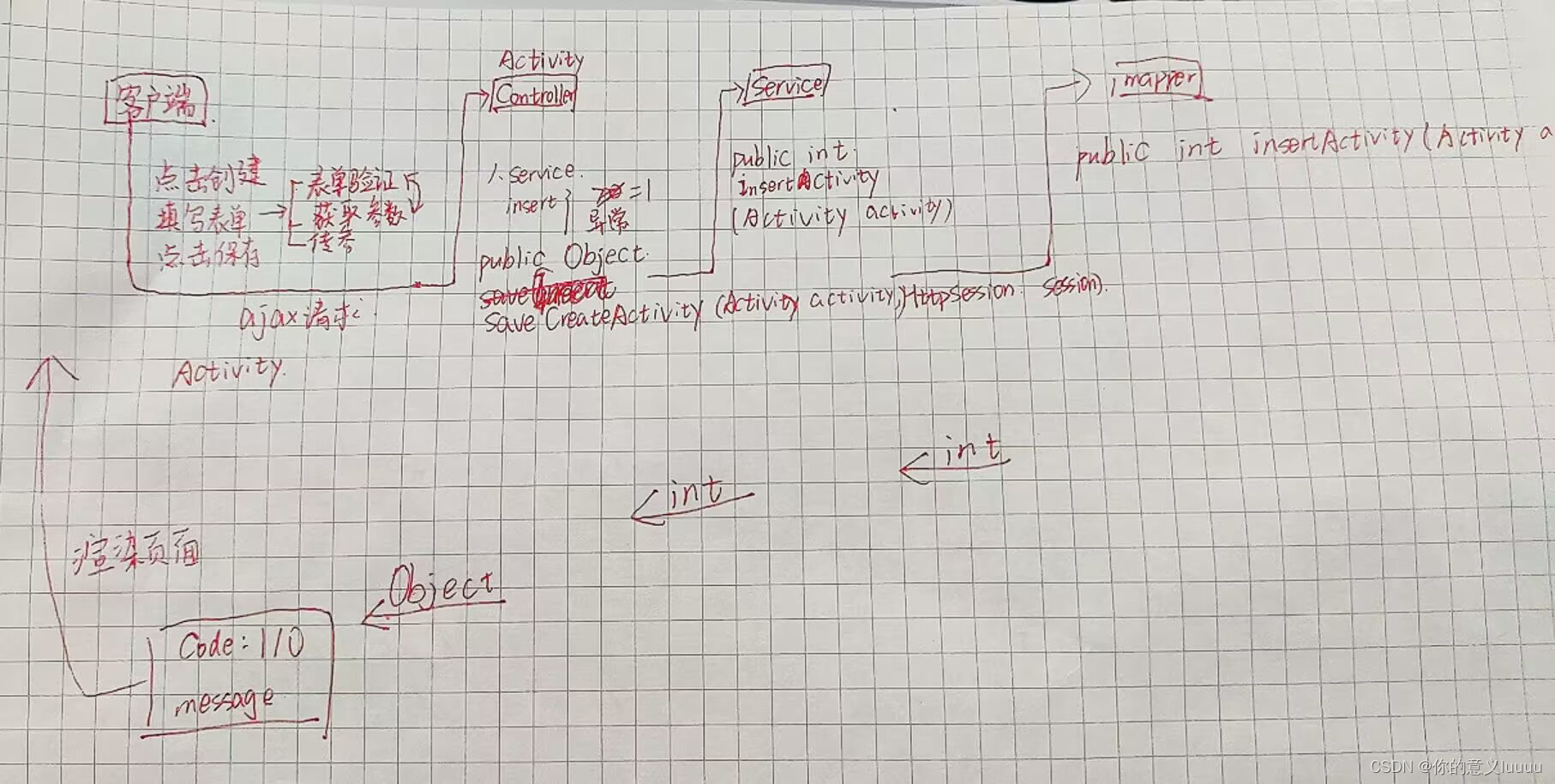
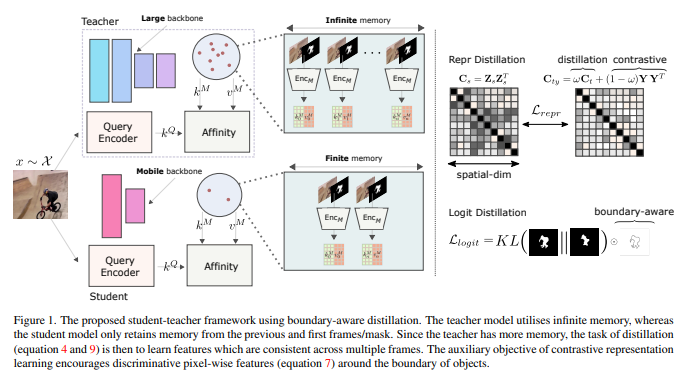
在嵌入式项目物联仓储系统中,使用cortexM0模拟仓库,cortex-A9模拟服务器,两块开发板之间使用ZigBee技术实现数据接收和发送,本文就介绍一下ZigBee组网的原理和相关步骤。
1.组网概述
组建一个完整的zigbee网状网络包括两个步骤:网络初始化、节点加入网络。其中节点加入网络又包括两个步骤:通过与协调器连接入网和通过已有父节点入网。
ZigBee网络中的节点主要包含三个:终端节点、路由器节点、PAN协调器节点
节点功能:
协调器节点:ZigBee协调器是网络各节点信息的汇聚点,是网络的核心节点,负责组建、维护和管理网络,并通过串口实现各节点与上位机的数据传递;ZigBee协调器有较强的通信能力、处理能力和发射能力,能够把数据发送至远程控制端。
路由器节点:负责转发数据资料包,进行数据的路由路径寻找和路由维护,允许节点加入网络并辅助其子节点通信;路由器节点是终端节点和协调器节点的中继,它为终端节点和协调器节点之间的通信进行接力。
终端节点:终端节点可以直接与协调器节点相连,也可以通过路由器节点与协调器节点相连。
2. 网络初始化预备
Zigbee网络的建立是由网络协调器发起的,任何一个zigbee节点要组建一个网络必须要满足以下两点要求:
(1)节点是FFD节点,具备zigbee协调器的能力;
(2)节点还没有与其他网络连接,当节点已经与其他网络连接时,此节点只能作为该网络的子节点,因为一个zigbee网络中有且只有一个网络协调器。
FFD:Full Function Device 全功能节点
RFD:Reduced FunctionDevice 半功能节点
全功能设备(FFD):设备可提供全部的IEEE 802.15.4 MAC服务,可充当热河ZigBee设备,因此FFD设备不仅可以发送和接收数据,还具备路由功能。
精简功能设备(RFD):设备只提供部分的IEEE 802.15.4 MAC服务,智能充当终端节点,不能充当协调点和路由节点,因此它只负责将采集的数据信息发送给协调点和路由点,并不具备数据转发、路由发现和路由维护等功能。
3.网络初始化流程
ZigBee网络初始化只能是由网络协调器发起的,在组建网络前,需要判断本节点还没与其他网络连接,如果节点已经与其他网络连接时,此节点只能作为该网络的子节点。一个ZigBee网络中有且仅有一个ZigBee协调器,一旦网络建立好了,协调器就退化成路由器的角色,甚至是可以去掉协调器的,这一切得益于ZigBee网络的分布式特性。
3.1 确定网络协调器:
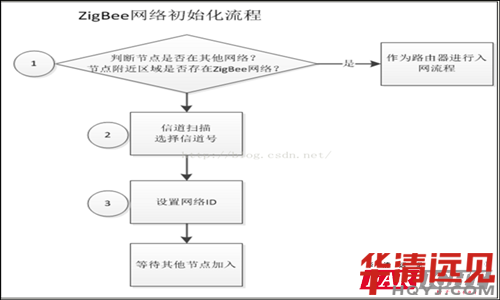
首先判断节点是否是FFD节点,接着判断此FFD节点是否在其他网络里或者网络里是否已经存在协调器。通过主动扫描,发送一个信标请求命令(Beaconrequest command),然后设置一个扫描期限(T_scan_duration),如果在扫描期限内都没有检测到信标,那么就认为FFD在其pos内没有协调器,那么此时就可以建立自己的zigbee网络,并且作为这个网络的协调器不断地产生信标并广播出去。
注意:一个网络里,有且只能有一个协调器(coordinator)。
3.2 进行信道扫描过程。
包括能量扫描和主动扫描两个过程:首先对指定的信道或者默认的信道进行能量检测,以避免可能的干扰。以递增的方式对所测量的能量值进行信道排序,抛弃那么些能量值超出了可允许能量水平的信道,选择可允许能量水平的信道并标注这些信道是可用信道。接着进行主动扫描,搜索节点通信半径内的网络信息。这些信息以信标帧的形式在网络中广播,节点通过主动信道扫描方式获得这些信标帧,然后根据这些信息,找到一个好的、相对安静的信道,通过记录的结果,选择一个信道,该信道应存在少的zigbee网络,好是没有zigbee设备。在主动扫描期间,MAC层将丢弃PHY层数据服务接收到的除信标以外的所有帧。
3.3 设置网络ID。
找到合适的信道后,协调器将为网络选定一个网络标识符(PAN ID,取值《=0x3FFF),这个ID在所使用的信道中必须是唯一的,也不能和其他zigbee网络冲突,而且不能为广播地址0xFFFF(此地址为保留地址,不能使用)。PAN ID可以通过侦听其他网络的ID然后选择一个不会冲突的ID的方式来获取,也可以人为的指定扫描的信道后,来确定不和其他网络冲突的PAN ID。
在zigbee网络中有两种地址模式:扩展地址(64位)和短地址(16位),其中扩展地址由IEEE组织分配,用于唯一的设备标识;短地址用于本地网络中设备标识,在一个网络中,每个设备的短地址必须唯一,当节点加入网络时由其父节点分配并通过使用短地址来通信。对于协调器来说,短地址通常设定为0x0000。
上面步骤完成后,就成功初始化了zigbee网状网络,之后就等待其他节点的加入。节点入网时将选择范围内信号强的父节点(包括协调器)加入网络,成功后将得到一个网络短地址并通过这个地址进行数据的发送和接收,网络拓扑关系和地址就会保存在各自的flash中。
4.节点通过协调器加入网络
当节点协调器确定之后,节点首先需要和协调器建立连接加入网络。
为了建立连接,FFD节点需要向协调器提出请求,协调器接收到节点的连接请求后根据情况决定是否允许其连接,然后对请求连接的节点做出响应,节点与协调器建立连接后,才能实现数据的收发。节点加入网络的具体流程可以分为下面的步骤:
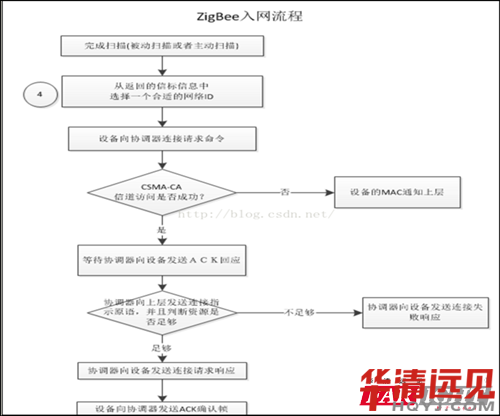
4.1 查找网络协调器。
首先会主动扫描查找周围网络的协调器,如果在扫描期限内检测到信 标,那么将获得了协调器的有关信息,这时就向协调器发出连接请求。在选择合适的网络之后,上层将请求MAC层对物理层PHY和MAC层的phyCurrentChannel、macPANID等PIB属性进行相应的设置。如果没有检测到,间隔一段时间后,节点重新发起扫描。
4.2 发送关联请求命令(Associaterequest command)。
节点将关联请求命令发送给协调器,协调器收到后立即回复一个确认帧(ACK),同时向它的上层发送连接指示原语,表示已经收到节点的连接请求。但是这并不意味着已经建立连接,只表示协调器已经收到节点的连接请求。当协调器的mac层的上层接收到连接指示原语后,将根据自己的资源情况(存储空间和能量)决定是否同意此节点的加入请求,然后给节点的mac层发送响应。
4.3 等待协调器处理。
当节点收到协调器加入关联请求命令的ACK后,节点mac将等待一段时间,接受协调器的连接响应。在预定的时间内,如果接收到连接响应,它将这个响应向它的上层通告。而协调器给节点的mac层发送响应时会设置一个等待响应时间(T_ResponseWaitTime)来等待协调器对其加入请求命令的处理,若协调器的资源足够,协调器会给节点分配一个16位的短地址,并产生包含新地址和连接成功状态的连接响应命令,则此节点将成功的和协调器建立连接并可以开始通信。若协调器资源不够,待加入的节点将重新发送请求信息,直接入网成功。
4.4 发送数据请求命令。
如果协调器在响应时间内同意节点加入,那么将产生关联响应命令(Associateresponse command)并存储这个命令。当响应时间过后,节点发送数据请求命令(Datarequest command)给协调器,协调器收到后立即回复ACK,然后将存储的关联响应命令发给节点。如果在响应时间到后,协调器还没有决定是否同意节点加入,那么节点将试图从协调器的信标帧中提取关联响应命令,成功的话就可以入网成功,否则重新发送请求信息直到入网成功。
4.5 回复。
节点收到关联响应命令后,立即向协调器回复一个确认帧(ACK),以确认接收到连接响应命令,此时节点将保存协调器的短地址和扩展地址,并且节点的MLME向上层发送连接确认原语,通告关联加入成功的信息。
5.节点通过已有节点加入网络
当靠近协调器的FFD节点和协调器关联成功后,处于这个网络范围内的其他节点就以这些FFD节点作为父节点加入网络了,具体加入网络有两种方式,一种是通过关联(associate)方式,就是待加入的节点发起加入网络;另一种是直接(direct)方式,就是待加入的节点具体加入到那个节点下,作为该节点的子节点。其中关联方式是zigbee网络中新节点加入网络的主要途径。
对于一个节点来说只有没有加入过网络的才能进行加入网络。在这些节点中,有些是曾经加入过网络中,但是却与它的父节点失去联系(这样的被称为孤儿节点),而有些则是新节点。当是孤儿节点时,在它的相邻表中存有原父节点的信息,于是它可以直接给原父节点发送加入网络的请求信息。如果父节点有能力同意它加入,于是直接告诉它的以前被分配的网络地址,它便入网成功;如果此时它原来的父节点的网络中,子节点数已达到大值,也就是说网络地址已经分配满,父节点便无法批准它加入,它只能以新节点身份重新寻找并加入网络。
而对于新节点来说,他首先会在预先设定的一个或多个信道上通过主动或被动扫描周围它可以找到的网络,寻找有能力批准自己加入网络的父节点,并把可以找到的父节点的资料存入自己的相邻表。存入相邻表的父节点的资料包括zigbee协议的版本、协议栈的规范、PAN ID和可以加入的信息。在相邻表中所有的父节点中选择一个深度小的,并对其发出请求信息,如果出现相同小深度的两个以上的父节点,那么随机选取一个发送请求。如果相邻表中没有合适的父节点的信息,那么表示入网失败,终止过程。如果发出的请求被批准,那么父节点同时会分配一个16位的网络地址,此时入网成功,子节点可以开始通信。如果请求失败,那么重新查找相邻表,继续发送请求信息,直到加入网络。
6.ZigBee分离流程
正常的分离过程:
1).协调器主动要求设备分离
协调器向设备发送接触连接命令,不管设备是否有ACK回应,协调器都认为该设备已经分离
2).已连接设备主动分离
设备主动向协调器发送接触连接命令,不管有没有收到协调器的ACK回应,设备都认为自己已经分离
3).异常分离过程
由于设备突然断电或者被阻挡覆盖,而造成的分离。前一种,在重启后,会发起孤儿请求连接。后一种,设备会尝试重试重传并等待ACK响应,如果没有响应,设备则为认为自己已经失去联系,间隔一段时间(默认为1s)后,节点重新并且不断的发起扫描。
对嵌入式物联网感兴趣的小伙伴,可以多了解一下相关信息。(看过来)